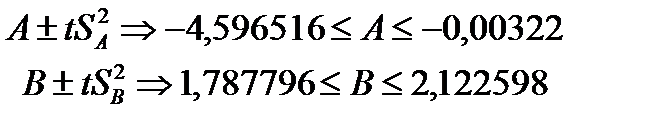Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Этап4. Проверка гипотезы по критерию Колмогорова.Содержание книги
Поиск на нашем сайте 1. Вычислим статистику Колмогорова:
2. Выберем уровень значимости 3. Найдем
4. Вывод по первой части: опытные данные не подчиняются нормальному закону распределения. Часть 2. Корреляционный анализ Цель: исследовать корреляцию между двумя величинами. Этап 1. Входные данные. Этап 2.Построение корреляционного поля.
Этап 3.Нахождение n=53;
Этап 4. Проверка гипотезы о значимости коэффициента корреляции, используя критерий Стьюдента. Выдвинем 2 гипотезы: H0: H0: Возьмем уровень значимости Критерий с использованием распределения Стьюдента:
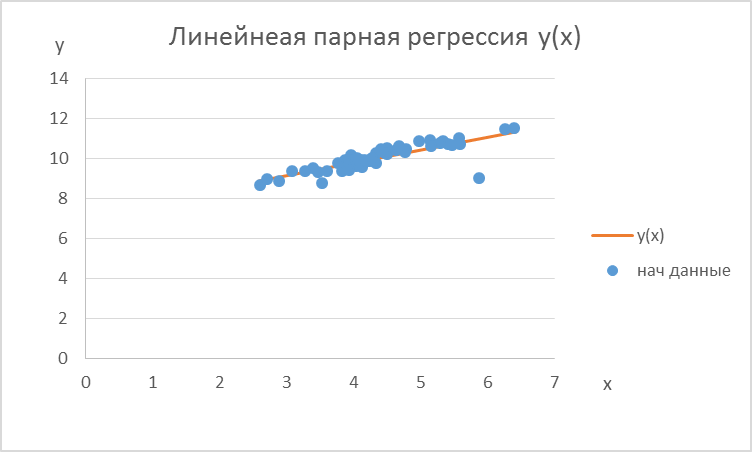
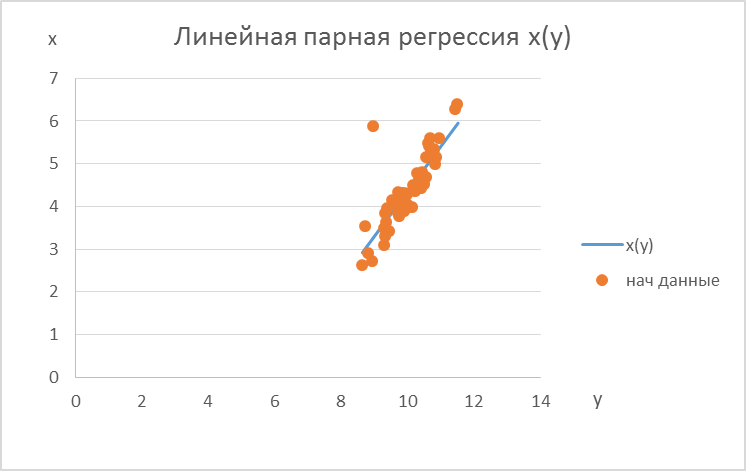
Следовательно, коэффициент корреляции статистически значим. Этап 5. Уравнение прямых регрессий. Построим уравнение регрессии yнаx:
y(x)=0,63981x+7,222643761
Построим уравнение регрессии xна y:
x(y)=1,0651405y+14,89165302.
Этап 6. Выборочные коэффициенты регрессии.
Этап 7. Нахождение доверительных интервалов прямых регрессий.
Вывод по второй части: Между двумя величинами x и y коэффициент корреляции Часть 3.Регрессионный анализ
Цель: по исходным данным построить две линейные по параметрам и нелинейные по переменным модели, приведя их преобразованиями к линейному виду. Входные данные:
Этап 1. Линеаризация данных. Проведем линеаризацию входных данныхв виде: 1. ln(y)=ln(a)-bln(x) Y=A-bX, гдеY=ln(y), A=ln(a), X=ln(x).
2. ln(y)=ln(a)-xln(b) Y=A-Bx, гдеY=ln(y), A=ln(a), B=ln(b). ‘
Этап 2. Нахождение точечных оценок параметров регрессии. 1.
2. Этап 3. Проверка значимости параметров Выдвинем две гипотезы: H0: b1=0(оценка не значима) H1: 1.
Построим уравнение регрессии: y=0,100272/x^(-1,9552)
2.
Построим уравнение регрессии: y=19,11082/1,047754^(-x)
Этап 4. Построение доверительных интервалов для параметров регрессии. 1. 2.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-06-14; просмотров: 124; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 ,
, 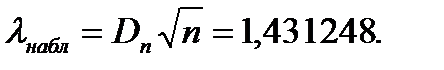 .
.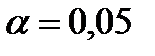 .
. как корень уравнения
как корень уравнения 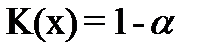 , где K(x) - функция Колмогорова.
, где K(x) - функция Колмогорова.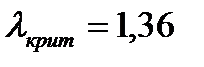 .
. , следовательно, гипотеза H0 отвергается.
, следовательно, гипотеза H0 отвергается.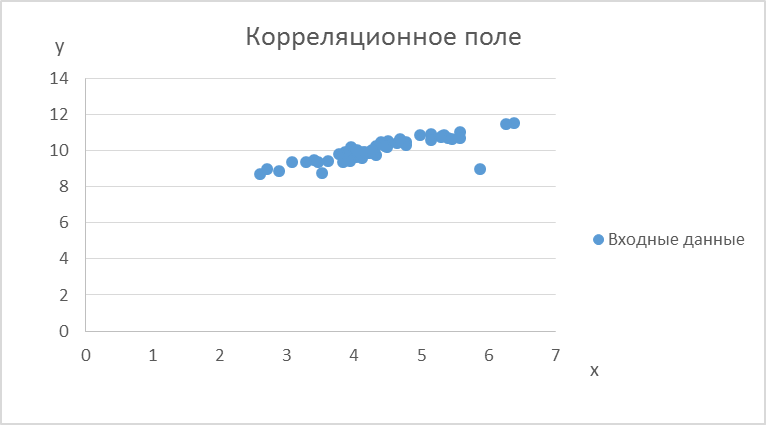
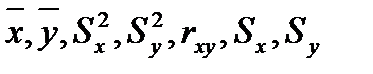 .
.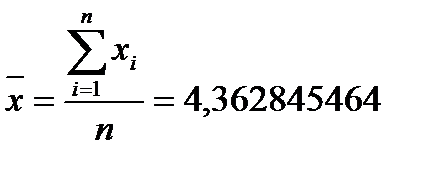 - несмещенная оценка мат. ожидания для x;
- несмещенная оценка мат. ожидания для x;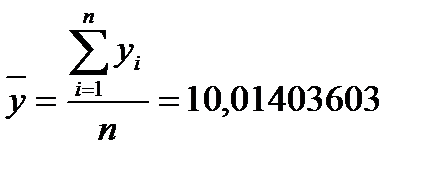 - несмещенная оценка мат. ожидания для y;
- несмещенная оценка мат. ожидания для y;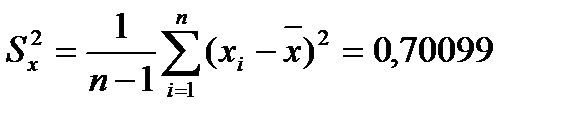 - несмещенная оценка дисперсии для x;
- несмещенная оценка дисперсии для x;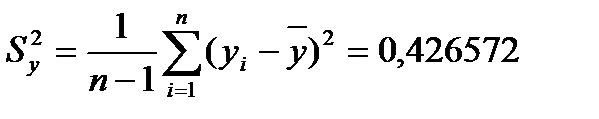 - несмещенная оценка дисперсии для y;
- несмещенная оценка дисперсии для y; - оценка дисперсии для x;
- оценка дисперсии для x;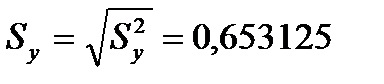 - оценка дисперсии для y;
- оценка дисперсии для y;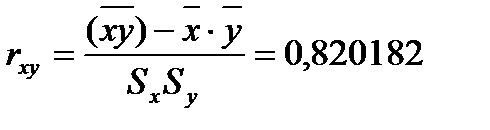 - выборочный коэффициент корреляции.
- выборочный коэффициент корреляции.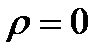 (коэффициент корреляции не значим);
(коэффициент корреляции не значим); (коэффициент корреляции значим).
(коэффициент корреляции значим).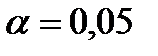 .
.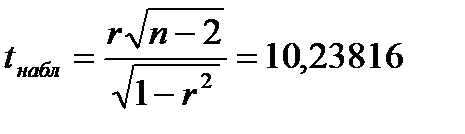
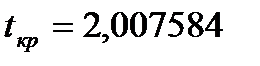
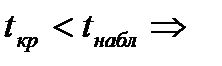 гипотеза H0отвергается.
гипотеза H0отвергается.
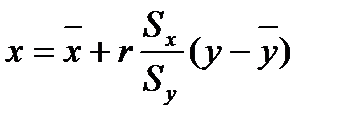
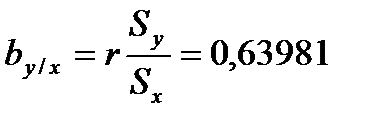 - выборочный коэффициент регрессии y на x.
- выборочный коэффициент регрессии y на x.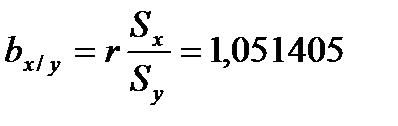 - выборочный коэффициент регрессии x на y.
- выборочный коэффициент регрессии x на y.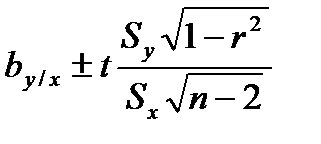 , где t=2,007584
, где t=2,007584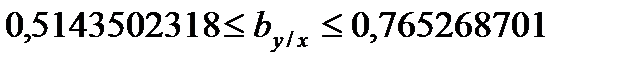
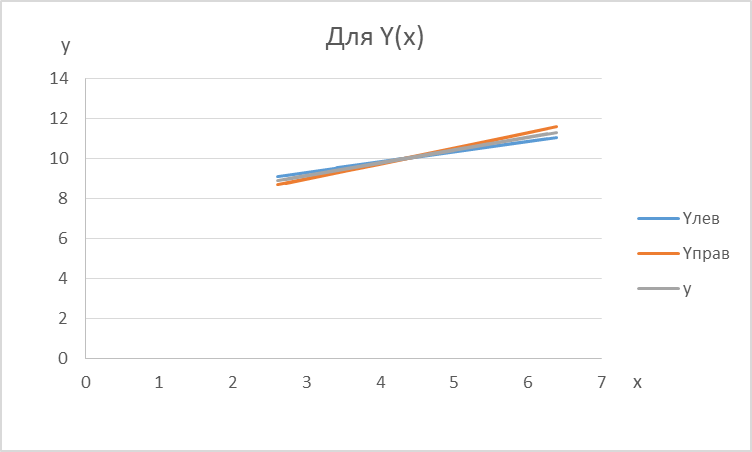
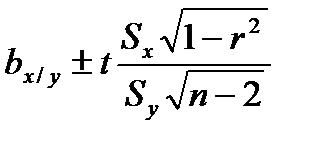
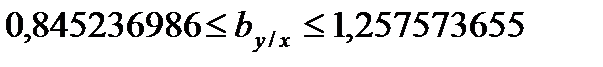

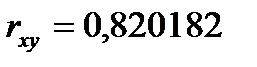 , следовательно, между ними корреляционная зависимость есть и она высока. Линейное уравнение y(x) лучше описывает регрессионную связь, чем уравнение x(y).
, следовательно, между ними корреляционная зависимость есть и она высока. Линейное уравнение y(x) лучше описывает регрессионную связь, чем уравнение x(y).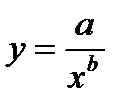
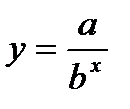
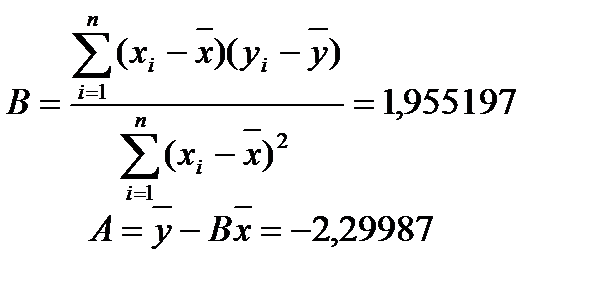
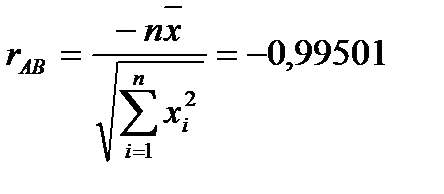 - коэффициент корреляции между Aи B
- коэффициент корреляции между Aи B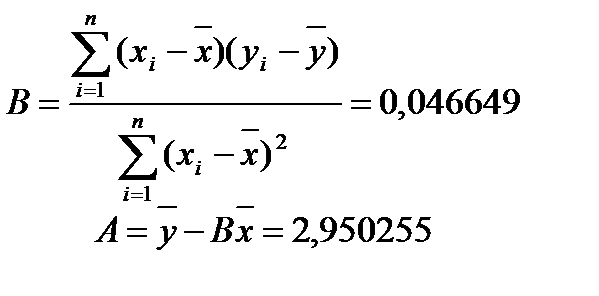
 и
и  .
.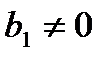 (оценка значима)
(оценка значима)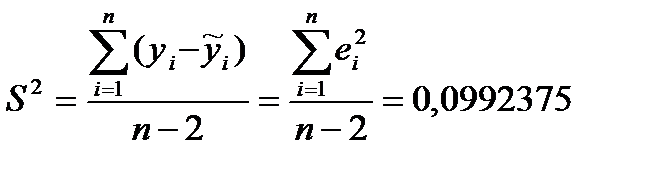 - остаточная(необъяснимая) дисперсия
- остаточная(необъяснимая) дисперсия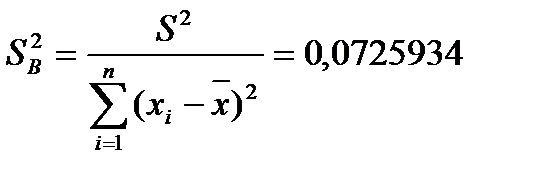
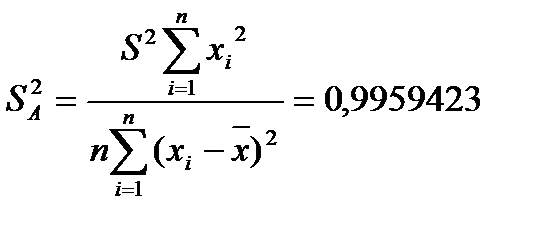
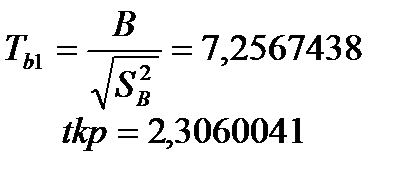
 гипотеза H0 отвергается, тогда оценка b1 значима.
гипотеза H0 отвергается, тогда оценка b1 значима.
 гипотеза H0принимается, тогда оценка a1не значима.
гипотеза H0принимается, тогда оценка a1не значима.
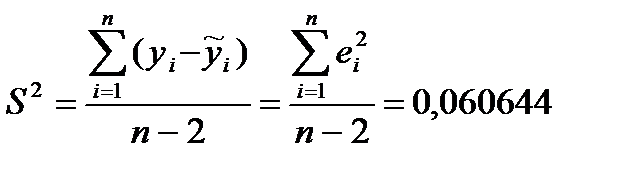 - остаточная(необъяснимая) дисперсия
- остаточная(необъяснимая) дисперсия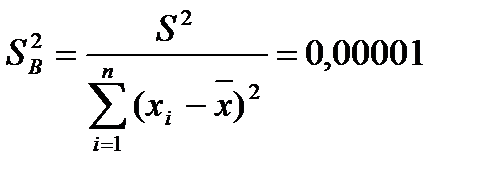
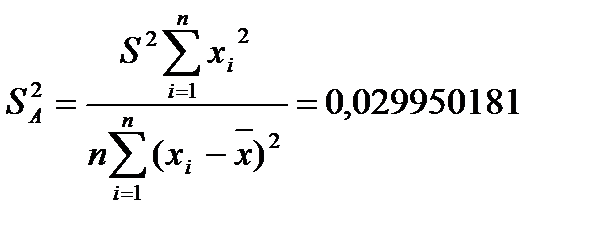
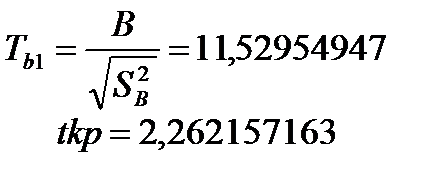
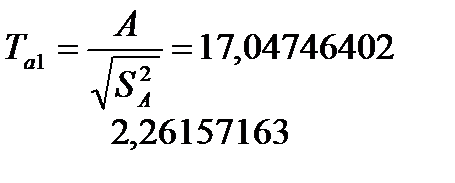
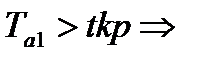 гипотеза H0отвергает, тогда оценка a1 значима.
гипотеза H0отвергает, тогда оценка a1 значима.