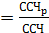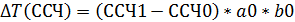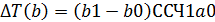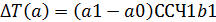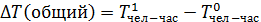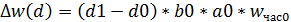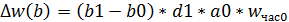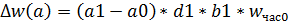Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эмпирический коэффициент детерминации и эмпирическое корреляционное отношениеСодержание книги
Поиск на нашем сайте Сводка и группировка Формула Стерджесса (для определения числа групп): Определение величины интервала группировки (если равные): Частота - численность отдельных вариантов ( Частость - частоты, выражаемые в долях единицы или в процентах
Средние величины Средняя арифметическая простая: Средняя арифметическая взвешенная: Средняя гармоническая взвешенная: Мода: Где Медиана:
Квартили:
Децили:
Показатели вариации Абсолютные показатели вариации: Размах вариации: Простое среднее линейное отклонение: Взвешенное среднее линейное отклонение: Простая дисперсия: Взвешенная дисперсия: Среднее квадратическое отклонение:
Относительные показатели вариации: Коэффициент осцилляции: Относительное линейное отклонение: Коэффициент вариации:
Эмпирический коэффициент детерминации и эмпирическое корреляционное отношение 1. Определить общее среднее значение показателя ( 2. Определить общую дисперсию ( 3. По каждой группе рассчитать групповые средние (как в п. 1, только по группам) 4. По каждой группе рассчитать групповые дисперсии (как п. 2, только по группам) 5. Вычислить среднюю из внутригрупповых дисперсий:
6. Определяется межгрупповая дисперсия:
7. Правило сложения дисперсий:
8. Вычисляется эмпирический коэффициент детерминации:
9. Рассчитывается эмпирическое корреляционное отношение:
Приложение к алгоритму Шкала Чеддока: До 0,3 связь слабая или её практически нет 0,3 - 0,5 связь средняя 0,5 - 0,7 связь достаточная 0,7 - 0,9 связь высокая 0,9 - 0,99 связь весьма высокая Выборочное наблюдение Находим среднее значение: 1. Выборочная средняя:
Выборочная дисперсия:
2. Средняя ошибка выборки:
Где N – объём генеральной совокупности n – объём выборочной совокупности Если N нет, но есть доля отбора, то 3. Предельная ошибка выборки:
4. Доверительные границы для среднего:
Вывод: с вероятность … можно утверждать, что в генеральной совокупности объектов средний … не ниже, чем … (нижняя граница интервала), не выше, чем … (верхняя граница интервала).
6. Находим генеральную долю: 1. Выборочная доля:
n – объём выборки, численность выборочной совокупности 2. Дисперсия доли:
3. Средняя ошибка выборки:
4. Предельная ошибка выборки:
5. Доверительные границы для доли:
*вероятность перевести в проценты (напр, р от 34% до 46%) Коэффициент Фехнера
u – число пар, у которых знаки отклонений значений показателей от их средних совпадают v – число пар, у которых знаки отклонений значений показателей от их средних не совпадают Отриц знач коэф – обратная связь, полож – прямая, 0 – отсутствует связь между признаками.
Коэффициент корреляции рангов Спирмена
n – число наблюдений
0 – связи нет, положит – прямая, отриц – обратная
Ряды динамики Средний уровень динамического ряда: 1. Интервальный ряд с равными промежутками между соседними датами – средняя арифметическая простая: 2. Интервальный ряд с неравными промежутками между соседними датами – средняя арифметическая взвешенная: 3. Ряд моментный с равными временными промежутками между соседними датами – средняя хронологическая простая: (если дни, то моментный ряд) 4. Ряд моментный с неравными временными промежутками между соседними датами – средняя хронологическая взвешенная:
Приросты и темп роста Абсолютные приросты:
Средний абсолютный прирост:
Темпы роста: Цепные: Базисные: Средний темп роста:
Темпы прироста получают путем вычитания из темпов роста 100%.
Индексы q – количество единиц данного типа продукции p – цена единицы продукции z – себестоимость единицы продукции p*q – товарооборот z*q – затраты на производство; общая себестоимость; издержки производства
Индивидуальный индекс цен: Индивидуальный индекс физического объема продукции: Индивидуальный индекс себестоимости: Индивидуальный индекс стоимости (товарооборота): Индивидуальный индекс затрат на производство:
Агрегатный индекс стоимости (товарооборота): Агрегатный индекс физического объёма продукции (товарооборота):
Агрегатный индекс цен: Агрегатный индекс издержек производства: Агрегатный индекс физического объёма продукции: Агрегатный индекс себестоимости:
Взаимосвязь:
14. Средние индексы: Средний арифметический индекс физ. объёма продаж (товарооборота):
Статистика населения
Оценка численности населения: Где Среднегодовая численность населения:
Естественный прирост населения: N-M Относительные показатели естественного движения населения:
Где
16. Относительные показатели миграционного движения:
Коэффициент общего прироста населения:
Статистика рынка труда Абсолютные показатели: 1) Трудоспособное население = население в трудоспособном возрасте – инвалиды 1,2 групп, находящиеся в трудоспособном возрасте – пенсионеры трудоспособного возраста 2) Трудовые ресурсы = трудоспособное население + работающие подростки до 15 лет + работающие пенсионеры 3) Экономически активное население = занятые + безработные
Относительные показатели:
Статистика оплаты труда
Взаимосвязь:
a – ср. фактическая продолжит. раб. дня
У индексов ниже такая же взаимосвязь, как и у этих показателей
Дополнение: Изменение количества отработанного времени за счёт различных факторов:
Изменение мес. выработки за счёт отдельных факторов:
Сводка и группировка Формула Стерджесса (для определения числа групп): Определение величины интервала группировки (если равные): Частота - численность отдельных вариантов ( Частость - частоты, выражаемые в долях единицы или в процентах
Средние величины Средняя арифметическая простая: Средняя арифметическая взвешенная: Средняя гармоническая взвешенная: Мода: Где Медиана:
Квартили:
Децили:
Показатели вариации Абсолютные показатели вариации: Размах вариации: Простое среднее линейное отклонение: Взвешенное среднее линейное отклонение: Простая дисперсия: Взвешенная дисперсия: Среднее квадратическое отклонение:
Относительные показатели вариации: Коэффициент осцилляции: Относительное линейное отклонение: Коэффициент вариации:
Эмпирический коэффициент детерминации и эмпирическое корреляционное отношение 1. Определить общее среднее значение показателя ( 2. Определить общую дисперсию ( 3. По каждой группе рассчитать групповые средние (как в п. 1, только по группам) 4. По каждой группе рассчитать групповые дисперсии (как п. 2, только по группам) 5. Вычислить среднюю из внутригрупповых дисперсий:
6. Определяется межгрупповая дисперсия:
7. Правило сложения дисперсий:
8. Вычисляется эмпирический коэффициент детерминации:
9. Рассчитывается эмпирическое корреляционное отношение:
Приложение к алгоритму Шкала Чеддока: До 0,3 связь слабая или её практически нет 0,3 - 0,5 связь средняя 0,5 - 0,7 связь достаточная 0,7 - 0,9 связь высокая 0,9 - 0,99 связь весьма высокая Выборочное наблюдение Находим среднее значение: 1. Выборочная средняя:
Выборочная дисперсия:
2. Средняя ошибка выборки:
Где N – объём генеральной совокупности n – объём выборочной совокупности Если N нет, но есть доля отбора, то 3. Предельная ошибка выборки:
4. Доверительные границы для среднего:
Вывод: с вероятность … можно утверждать, что в генеральной совокупности объектов средний … не ниже, чем … (нижняя граница интервала), не выше, чем … (верхняя граница интервала).
6. Находим генеральную долю: 1. Выборочная доля:
n – объём выборки, численность выборочной совокупности 2. Дисперсия доли:
3. Средняя ошибка выборки:
4. Предельная ошибка выборки:
5. Доверительные границы для доли:
*вероятность перевести в проценты (напр, р от 34% до 46%)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-19; просмотров: 126; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |

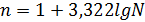 , где n – число групп, N – число единиц совокупности
, где n – число групп, N – число единиц совокупности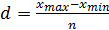 (макс. значение признака совокупности, n – количество групп)
(макс. значение признака совокупности, n – количество групп)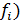
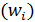
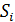 – накопленная частота (постепенное суммирование
– накопленная частота (постепенное суммирование 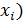
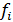 )
)
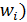
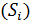
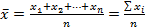 (несгруппиров.), где
(несгруппиров.), где 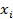 – варианты, n – объем совокупности
– варианты, n – объем совокупности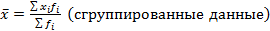
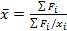
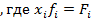 (фонд з/п, например, вся продукция)
(фонд з/п, например, вся продукция)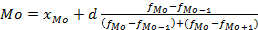 (интервальный ряд с равными интервалами; наиболее часто встречающееся значение признака)
(интервальный ряд с равными интервалами; наиболее часто встречающееся значение признака)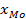 - нижняя граница модального интервала, d – величина интервала,
- нижняя граница модального интервала, d – величина интервала, 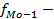 частота интервала, предшествующего модальному,
частота интервала, предшествующего модальному, 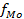 – частота модального интервала…
– частота модального интервала…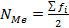 (вычисление порядкового номера медианы; далее выбираем накопленную частоту, превышающую порядковый номер)
(вычисление порядкового номера медианы; далее выбираем накопленную частоту, превышающую порядковый номер)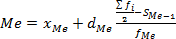 (интервальный ряд)
(интервальный ряд)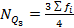 (на 4 равные части)
(на 4 равные части)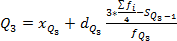 (если 3 квартиль)
(если 3 квартиль)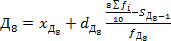 (если 8 дециль)
(если 8 дециль)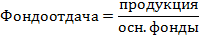
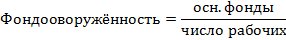
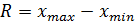
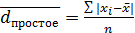 (если нет частоты)
(если нет частоты)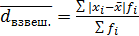
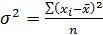 (несгруппированные данные, т.е. нет частоты)
(несгруппированные данные, т.е. нет частоты)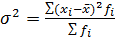 (есть частота)
(есть частота)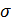 (корень из дисперсии)
(корень из дисперсии)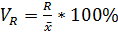
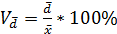
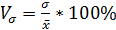
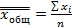 )
)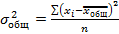 )
)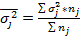 (n – количество иксов)
(n – количество иксов)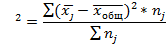
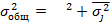
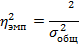
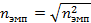 (от 0 до 1)
(от 0 до 1)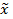 =
= 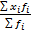
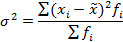
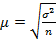 (при повторной случайной выборке)
(при повторной случайной выборке)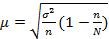 (при бесповторной случайной и механической выборке)
(при бесповторной случайной и механической выборке) – доля отбора в коэффициентах.
– доля отбора в коэффициентах.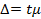 где t – коэф. доверия (находится по таблице)
где t – коэф. доверия (находится по таблице)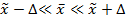 (серединка остается буквой)
(серединка остается буквой)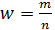 где m – число единиц, удовлетворяющих заданному условию
где m – число единиц, удовлетворяющих заданному условию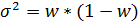
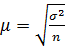 ( выборка повторная)
( выборка повторная)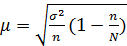 (бесповторная случайная и механическая выборка)
(бесповторная случайная и механическая выборка)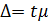 где t – коэф. доверия (находится по таблице)
где t – коэф. доверия (находится по таблице)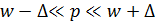 (где p – генеральная доля, остается буквой)
(где p – генеральная доля, остается буквой)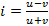 (от -1 до 1)
(от -1 до 1)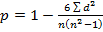 (буква ро; от -1 до 1)
(буква ро; от -1 до 1)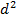 – квадрат разности рангов для каждого наблюдения (ранг – номер икса в таблице по возрастанию)
– квадрат разности рангов для каждого наблюдения (ранг – номер икса в таблице по возрастанию)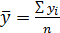
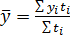 , где
, где 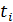 – временной промежуток между соседними датами
– временной промежуток между соседними датами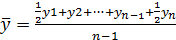
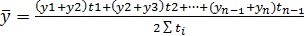 , где
, где 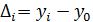 – базисные приросты, где
– базисные приросты, где 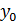 – базисный уровень (часто первый)
– базисный уровень (часто первый)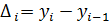 – цепные приросты
– цепные приросты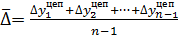 , где
, где 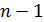 – число абсолютных приростов
– число абсолютных приростов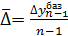 , где в числителе последний рассчитанный базисный абсолютный прирост
, где в числителе последний рассчитанный базисный абсолютный прирост 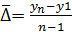 , где
, где 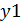 – первый уровень динамического ряда,
– первый уровень динамического ряда, 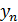 – последний уровень динамического ряда
– последний уровень динамического ряда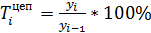
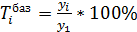
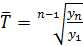
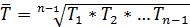
 (посл. рассчитанный базисный коэф роста)
(посл. рассчитанный базисный коэф роста)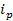 = p1/p0
= p1/p0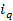 = q1/q0
= q1/q0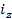 = z1/z0
= z1/z0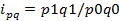
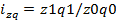
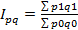
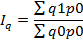
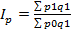
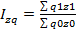
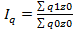
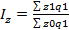
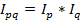
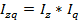
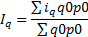
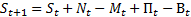
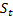 – численность населения в начале года
– численность населения в начале года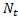 – число родившихся
– число родившихся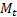 – число умерших
– число умерших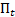 – число прибывших
– число прибывших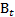 – число выбывших
– число выбывших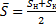 (данные на нач. и конец года)
(данные на нач. и конец года)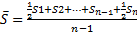 ( данные на нач. каждого месяца)
( данные на нач. каждого месяца)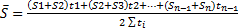 ( данные на нач. Месяца, неравно стоящих друг от друга), где t – временной промежуток между соседними датами, n – количество временных периодов
( данные на нач. Месяца, неравно стоящих друг от друга), где t – временной промежуток между соседними датами, n – количество временных периодов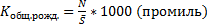
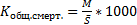
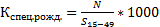 или
или 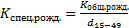
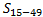 – среднегодовая численность женщин детородного возраста
– среднегодовая численность женщин детородного возраста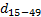 – доля женщин в возрасте от 15 до 49 в общей числ. Населения
– доля женщин в возрасте от 15 до 49 в общей числ. Населения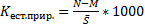 или
или 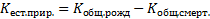
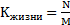 или
или 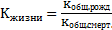
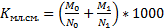 (младенч смертность), где N0 – родившиеся в предыдущем году, N1 – в данном году, М0 – умершие дети в возрасте до 1 года в данном году из поколения родившихся в предыдущем году, М0 – в данном году
(младенч смертность), где N0 – родившиеся в предыдущем году, N1 – в данном году, М0 – умершие дети в возрасте до 1 года в данном году из поколения родившихся в предыдущем году, М0 – в данном году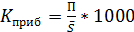
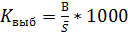
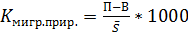 или
или 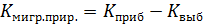
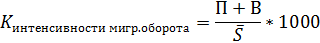
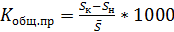 или
или 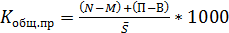
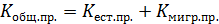
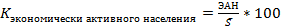
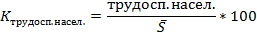
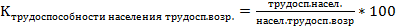
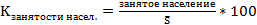
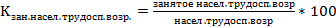
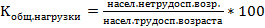
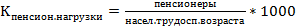
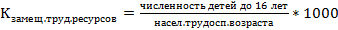
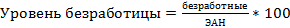
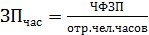
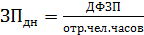
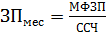
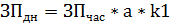
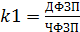
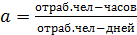
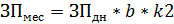
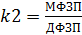
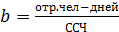
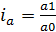
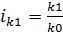 d
d