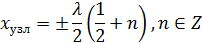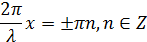Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамика гармонического колебания: ⇐ ПредыдущаяСтр 4 из 4
Уравнение гармонических колебаний в дифференциальной форме
ИЛИ
Решения этого уравнения:
Квазиупругая сила – сила пропорциональная смещению и возвращающая тело в положение равновесия. (Пример:
Пружинный маятник: a. Горизонтальный (
Второй закон Ньютона:
Отсюда
b. Вертикальный (Квазиупругая сила – равнодействующая силы тяжести и силы упругости)
Второй закон Ньютона при колебании:
Получили такое же уравнение, значит, вывод будет такой же как и в случае горизонтального пружинного маятника.
Математический маятник:
Основное уравнение динамики вращательного движения (
Так как
Отсюда
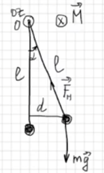
Физический маятник – твердое тело, совершающее под действием
Получим уравнения
Приведенной длиной физического маятника называется длина такого математического маятника, период которого совпадает с периодом колебания физического маятника.
Тогда
Динамика гармонического колебания: Уравнение гармонических колебаний в дифференциальной форме
ИЛИ
Решения этого уравнения:
Квазиупругая сила – сила пропорциональная смещению и возвращающая тело в положение равновесия. (Пример:
Линейный гармонический осциллятор – физическая система, совершающая колебания (ИЛИ это система, потенциальная энергия которой квадратично зависит от координаты).
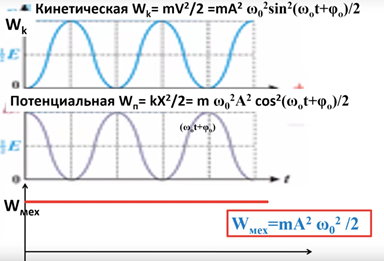
Кинетическая и потенциальная энергия гармонического осциллятора
Закон сохранения энергии
Дополнительно:
3.4. Пружинный маятник: a. Горизонтальный (
Второй закон Ньютона:
Отсюда
b. Вертикальный (Квазиупругая сила – равнодействующая силы тяжести и силы упругости)
Второй закон Ньютона при колебании:
Получили такое же уравнение, значит, вывод будет такой же как и в случае горизонтального пружинного маятника.
Математический маятник:
Основное уравнение динамики вращательного движения (
Так как
Отсюда
Физический маятник – твердое тело, совершающее под действием
Получим уравнения
Приведенной длиной физического маятника называется длина такого математического маятника, период которого совпадает с периодом колебания физического маятника.
Тогда
3.5. Волной называется процесс распространения колебаний в упругой среде (жидкой, газообразной).
Основные характеристики волн:
Механизм образования поперечной волны: (в газах и жидкостях не возникают)
Механизм образования продольных волн: Одна частица отдает импульс другим частицам, окружающим её
Волновое число:
Плоская волна — волна, поверхность постоянной фазы которой представляет собой плоскость. Фронт плоской волны неограничен по размерам, вектор фазовой скорости перпендикулярен фронту.
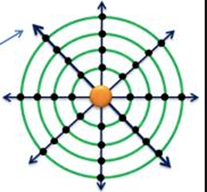
Сферическая волна — волна, фронт которой представляет собой сферу. Вектор фазовой скорости расходящейся сферической волны ориентирован в радиальном направлении от источника
Уравнение плоской бегущей волны:
В общем случае:
Вывод уравнения: (для
Волновое уравнение:
Вывод уравнения: (для случая
Первая и вторая производные по
Первая и вторая производные по
Используя
Если
где
3.6. Энергия волны Для выведения формул понадобятся величины:
Вывод:
Окончательно получим
Поток энергии -
Объемная плотность энергии
Плотность потока энергии
Вектор плотности потока энергии (вектор Умова)
Вывод формулы
Интенсивность волн
(Главный вывод: интенсивность волн прямо пропорциональна квадрату амплитуды)
Спектральная плотность потока излучения представляет собой поток излучения, приходящийся на малый единичный интервал спектра. Если переменной, определяющей положение точек спектра, является некоторая величина
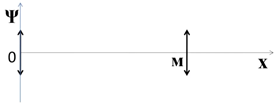
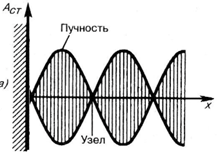
Уравнение стоячей волны
Амплитуда стоячей волны
Найдем координаты узлов и пучностей:
В узлах
Для пучностей
|
||||||
|
Последнее изменение этой страницы: 2021-07-19; просмотров: 690; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.253.221 (0.106 с.) |
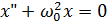
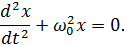
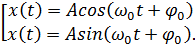
 )
)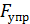 – квазиупругая сила)
– квазиупругая сила)
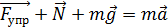
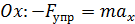
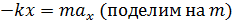
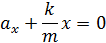
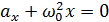

 и период колебаний такого маятника
и период колебаний такого маятника  .
.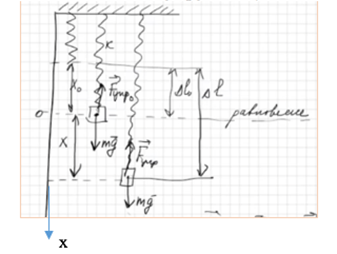
 В положении равновесия из второго закона Ньютона:
В положении равновесия из второго закона Ньютона: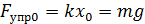
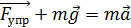
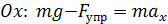

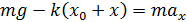



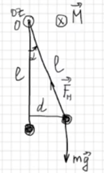
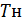 – сила натяжения нити):
– сила натяжения нити):
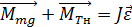
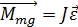
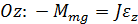
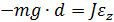
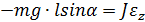
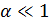 , то
, то 
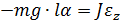

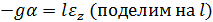
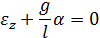
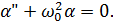
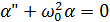 – уравнение гармонических колебаний для математического маятника, циклическая частота
– уравнение гармонических колебаний для математического маятника, циклическая частота 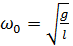 и период колебаний такого маятника
и период колебаний такого маятника 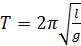 .
. колебания вокруг неподвижной горизонтальной оси, проходящей через точку
колебания вокруг неподвижной горизонтальной оси, проходящей через точку  , не совпадающей с ц. м. тела.
, не совпадающей с ц. м. тела.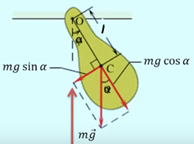



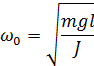
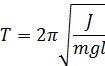

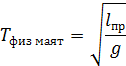


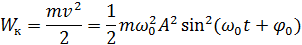
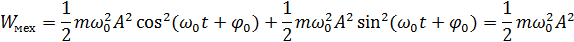
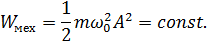




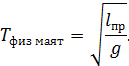





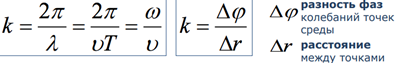




 – расстояние от точки
– расстояние от точки 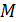
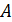 – амплитуда колебаний
– амплитуда колебаний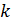 – волновое число, показывающее, чему равна разность фаз точек, находящихся на расстоянии 1 м
– волновое число, показывающее, чему равна разность фаз точек, находящихся на расстоянии 1 м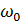 – циклическая частота
– циклическая частота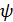 – смещение точки от положения равновесия
– смещение точки от положения равновесия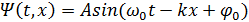
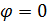 )
)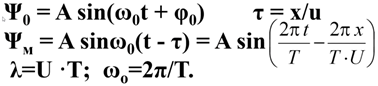
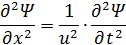
 )
)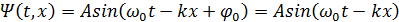
 :
: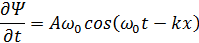

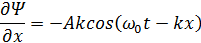
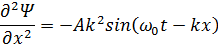

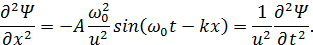

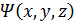 , то
, то
 – оператор Лапласа и
– оператор Лапласа и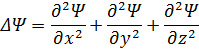
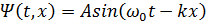

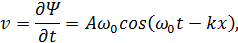
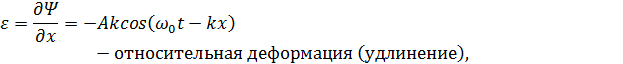

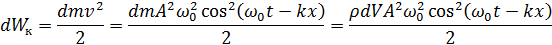
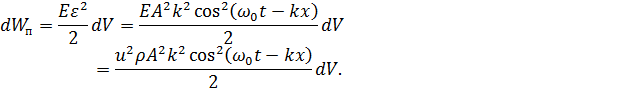
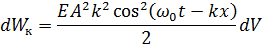
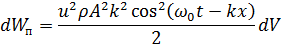
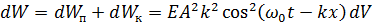

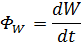
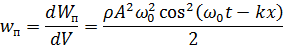
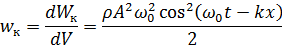
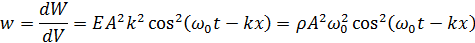



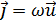
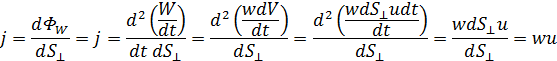

 , то соответствующая ей спектральная плотность потока излучения обозначается как
, то соответствующая ей спектральная плотность потока излучения обозначается как 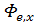 и определяется как
и определяется как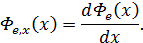

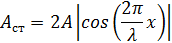
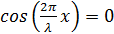 , то есть
, то есть