
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: «Условный оператор. Оператор многозначного ветвления»Содержание книги
Поиск на нашем сайте
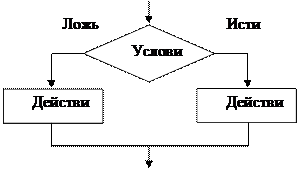
При описании разветвляющихся процессов обычно используют понятие условного и безусловного перехода. Если в программе требуется нарушить порядок выполнения операторов без предварительных проверок каких-либо условий, переход называется безусловным. Для реализации такого перехода служит оператор goto n (n – метка). В Паскале метка должна быть описана в разделе label, например: label m, metka, 123 Однако современный стиль программирования предполагает как можно более редкое применение безусловного перехода, а еще лучше - полный отказ от него. Условный оператор IF предназначен для изменения порядок выполнения операторов в зависимости от истинности или ложности некоторого условия. Он предписывает выполнять некоторое действие только в том случае, когда выполняется заданное условие. Это условие записывается в виде логического выражения, а действие, которое нужно выполнить, задается в виде последовательности операторов. Существует две конструкции оператора ветвления – простая и расширенная: Простая конструкция Расширенная конструкция
Полная развилка: If < условие> then < оператор 1 > else < оператор2 >; Укороченная развилка If < условие> then < оператор 1 >.
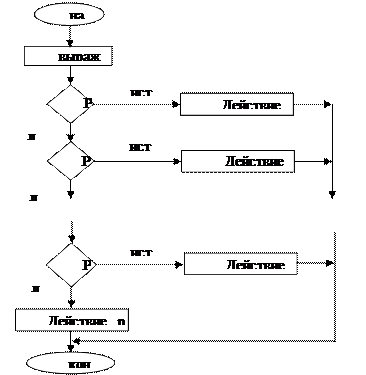
Оператор выбора CASE В случае необходимости разветвить вычислительный процесс в зависимости от выполнения или невыполнения того или иного условия на более чем две ветви используется оператор выбора (случая, селектора, переключателя). Его использование оказывается более удобным по сравнению с использованием оператора if. Case S of C1: <Оператор1> С2: <Оператор2> ................ CN: <ОператорN> Else <Оператор> End; S - выражение порядкового типа значение которого вычисляется; C1, C2,…,CN – константы, с которыми сравнивается значение выражения S; <Оператор1>, <Оператор2>, <Оператор N> - операторы, из которых выполняется тот, с константой которого совпадает значение выражения S. Ветвь оператора else является необязательной. Если она отсутствует и значение выражения S не совпадает ни с одной константой, весь оператор рассматривается как пустой. Если для нескольких констант нужно выполнить один и тот же оператор, их можно перечислить через запятую, сопроводив их одним оператором. Схематически такую конструкцию можно изобразить следующим образом:
Примеры решений задач 1. Даны действительные числа х и у. Получить max(x,y). Program maximum; Var x,y:real; Begin Write ('Введите х и у'); Readln (x,y); If x>y then m:=x else m:=y; Write (' Максимальное m=',m); End.
2. Ввести число от 1 до 100, если введенное число попадет в диапазон [1..10] определить его четность. Program Chisla; Var I: integer; Begin Write ('Введите число'); Readln (i); Case i of 2, 4, 6, 8: Writeln (‘Четная цифра’) 1, 3, 5, 7, 9: Writeln (‘Нечетная цифра’) 10..100: Writeln (‘Число от 10 до 100’) else Writeln (‘Отрицательное число или больше 100’) end; End. Список задач 1. Даны действительные числа x,y. Получить: а) max(x,y), б) min(x,y), в) max(x,y),min(x,y). 2. Даны действительные числа x, y, z. Вычислить: а) max(x + y + z, x · y · z), б) min2 (x + y + z/2, x · y · z) + 1. 3. Даны действительные числа a, b, c. Проверить выполняется ли неравенство a < b < c. 4. Найти min значение из трёх величин, определяемых арифметическими выражениями a = sin(x), b = cos(x), c = ln(x) при заданных значениях x. 5. Даны действительные числа a, b, c. Удвоить эти числа, если 6. Даны два действительных числа. Заменить первое число нулём, если оно меньше или равно второму, и оставить числа без изменения иначе. 7. Даны действительные числа x,y. Меньшее из этих двух чисел заменить их полусуммой, а большее – их удвоенным произведением. 8. Даны действительные числа a, b, c, d. Если a < b < c < d, то каждое число заменить наибольшим из них; если a > b > c > d, то числа оставить без изменения; иначе все числа заменяются их квадратами. 9. Даны действительные числа a, b, c. Выяснить, имеет ли уравнение ax2+bx+c=0 действительные корни. Если действительные корни имеются, то найти их. В противном случае ответом должно служить сообщение, что действительных корней нет. 10. Даны действительные положительные числа a, b, c, x, y. Выяснить, пройдёт ли кирпич с рёбрами a, b, c в прямоугольное отверстие со сторонами x и y. Просовывать кирпич в отверстие разрешается только так, чтобы каждое из рёбер было параллельно или перпендикулярно каждой из сторон отверстия. 11. Даны два действительных числа. Вывести первое число, если оно больше второго, и оба числа если это не так. 12. Даны три действительных числа. Выбрать из них те, которые принадлежат интервалу (1,3). 13. Даны три действительных числа. Возвести в квадрат те из них, значения которых не отрицательны. 14. Если сумма трёх попарно различных действительных чисел x,y,z меньше единицы, то наименьшее из этих трёх чисел заменить полусуммой двух других; иначе заменить меньшее из x и y полусуммой двух оставшихся значений. 15. Даны два числа. Если первое число больше второго по абсолютной величине, то необходимо уменьшить первое в 5 раз, иначе оставить числа без изменения. 16. Даны действительные положительные числа x, y, z. а) Выяснить, существует ли треугольник с длинами сторон x, y, z. б) Если треугольник существует, то ответить - является ли он остроугольным, тупоугольным или прямоугольным. 17. Даны действительные числа x1,x2,x3,y1,y2,y3. Принадлежит ли начало координат треугольнику с вершинами (x1,y1), (x2,y2), (x3,y3)? 18. Составить программу определения большей площади из двух фигур круга или квадрата. Известно, что сторона квадрата равна а, радиус круга равен r. Вывести и напечатать значение площади большей фигуры. 19. Даны действительные, положительные числа a,b,c,d. Выяснить, можно ли построить четырёхугольник с такими длинами сторон. 20. Определить, является ли целое число чётным. 21. Определить, верно ли, что при делении неотрицательного целого числа а на положительное целое число b, получается остаток равный одному из двух заданных чисел r или s. 22. Вывести значение y(x) в зависимости от введенного значения аргумента: а) в) д)
Практическая работа № 5 Тема: «Операторы повтора»
При реализации многократного повторения некоторых операций линейной конструкцией необходимо снова и снова повторять одни и те же операторы. Для более компактной реализации этих операций во всех языках используются циклические конструкции, суть которых заключается в том, что вместо многократного переписывания одних и тех же строк программы управление в нужном месте передается предыдущим операторам с тем, чтобы они повторялись. Имеется два вида циклических алгоритмов: цикл с предусловием (цикл ПОКА) и цикл с постусловием (цикл ДО). Оператор цикла REPEAT организует выполнение цикла, состоящего из любого числа операторов, с неизвестным заранее числом повторений. Тело цикла выполняется хотя бы один раз. Выход из цикла осуществляется при истинности некоторого логического выражения. Структура оператора: repeat <тело цикла> until <условие>; Оператор цикла WHILE организует выполнение одного оператора неизвестное заранее число раз. Выход из цикла осуществляется, если некоторое логическое выражение окажется ложным. Так как истинность логического выражения проверяется в начале каждого повтора, тело цикла может не выполняться ни разу. Структура оператора цикла имеет вид: while <условие> do <тело цикла>; Блок-схемы циклических конструкций могут быть изображены следующим образом:
Оператор цикла FOR организует выполнение одного оператора заранее известное число раз. Существует два варианта оператора. for <переменная>:=<нач. значение> to <кон. значение> do <оператор>; for <переменная>:=<нач. значение> downto <кон. значение>
Выполнение очередного повтора включает в себя сначала выполнение оператора, а затем присваивание переменной цикла следующего большего значения (в первом случае) или следующего меньшего (во втором варианте). Особенностью арифметического цикла является то, что число повторений операторов цикла должно быть известно заранее. Примеры решений задач. 1. Вычислить N! (факториал). Program Fak to rial; Var n, i, f: integer; Begin f:=1; Write ('Введите n='); Readln (n); For i:=2 to n do f:=f*i; Writeln (n,'!=',f); End.
2. Найти сумму цифр в записи данного натурального числа; Program SUM; Var a,b,s,k:Integer; Begin Readln (a); s:=0; While a<>0 do Begin b:=b mod 10; s:=s+b; a:= trunc (a/10); { a:= a div 10 } end; Writeln (s); End. Список задач 1. Дано натуральное число n. Получить все пифагоровы тройки натуральных чисел, каждое из которых не превосходит n, т.е. все такие тройки натуральных чисел a, b, c, что a2 + b2 = c2. 2. Дано натуральное число n. Найти все меньшие n числа Мерсенна. Число Мерсенна – это простое число, представленное в виде Mp=2p–1, где p – тоже простое число. 3. Два натуральных числа называют дружественными, если каждое из них равно сумме всех делителей другого, кроме самого этого числа. Найти все пары дружественных чисел, лежащих в диапазоне от 200 до 300. 4. Дано натуральное число n. Среди чисел 1, 2,..., n найти все такие, запись которых совпадает с последними цифрами записи их квадрата. 5. Назовём натуральное число палиндромом, если его запись читается одинаково как с начала так и с конца (пример: 4884, 393, 1, 22). а) найти все меньшие 100 натуральные числа, которые являются палиндромами; б)определить, является ли заданное натуральное число палиндромом; в) найти все меньшие 100 натуральные числа, которые при возведении в квадрат дают палиндром; г) найти все меньшие 100 натуральные числа-палиндромы, которые при возведении в квадрат дают палиндром; д) является ли число палиндромом с учётом чётных цифр; е) верно ли, что это число содержит ровно три одинаковые цифры; ж) верно ли, что все чётные цифры числа различны; 6. Дано натуральное число n (n>99). Определить число сотен в нём. 7. Дано натуральное число n (n<99). Выяснить, верно ли, что n2 равно кубу суммы цифр числа n. 8. Дано натуральное число n (n<9999). а) сколько цифр в числе n? б) чему равна сумма его цифр? в) найти последнюю цифру числа. г) найти первую цифру числа. д) найти предпоследнюю цифру числа (в предположении, что n>10). е) дано число m. Найти сумму m-последних цифр числа n. ж) выяснить, входит ли цифра 3 в запись числа n. з) поменять порядок цифр числа n на обратный. и) переставить последнюю и первую цифры числа n. к) приписать по единице в начало и конец записи числа n. 9. Является ли заданное натуральное число степенью двойки. 10. Разложить заданное число на простые множители. 11. Число, равное сумме всех своих делителей, включая единицу, называется совершенным. Найти и напечатать все совершенные числа в интервале от 2 до х. 12. Найти сумму квадратов чисел от m до n. 13. Найти сумму квадратов нечётных чисел в интервале, заданном значениями переменных m и n; 14. Найти сумму квадратов четных чисел в интервале, заданном значениями переменных m и n; 15. Найти сумму целых положительных чисел, кратных 4 и меньших 100. 16. Определить k - количество трёхзначных натуральных чисел, сумма цифр которых равна n (1,n,27). Операции деления, div и mod не использовать. Вложенные циклы 17. Дано натуральное число n. Получить все натуральные числа, меньшие n и взаимно просты с ним. 18. Даны целые числа p и q. Получить все делители числа q, взаимно простые с p. 19. Дано натуральное число n. Получить все простые делители этого числа. 20. Найти 100 первых простых чисел. 21. Даны натуральные числа n,m. Получить все меньшие n натуральные числа, квадрат суммы цифр которых равен m. 22. Натуральное число называется совершенным, если оно равно сумме всех своих делителей за исключением самого себя. Например, 6=1+2+3. Дано натуральное число n. Получить все совершенные числа, меньшие n. 23. Дано пять различных целых чисел. Найти среди них два числа, модуль разности которых имеет: а) наибольшее значение; б) наименьшее значение. 24. Вывести на экран числовой ряд действительных чисел от 10 до 20 с шагом 0,2. 25. Дано натуральное число n. Вычислить а) 2n; б) n!; в) an; г) a(a+1)…(a+n-1); д) a(a-n)(a-2n)…(a-n·n). е) ж) з) 26. Даны действительные числа x, а, натуральное число n. Вычислить 27. Дано действительное число a. Найти: а) среди чисел б) среди чисел 28. Даны действительные числа n и m. Найти наибольший делитель этих чисел, используя алгоритм Евклида. 29. Дано натуральное n. Найти 30. Дано натуральное число n. Вычислить 1·2+2·3·4+…+…+n·(n+1)·…·2n. 31. Вычислить 32. Даны натуральные числа n, k (n³k³0). Вычислить 33. Вычислить a) е) л) 34. Дано натуральное число n. Вычислить произведение первых n сомножителей: а) Практическая работа № 6
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 156; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.28.173 (0.012 с.) |


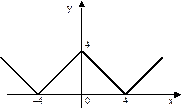 б)
б) 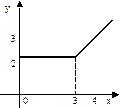
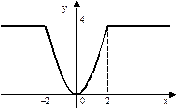 г)
г) 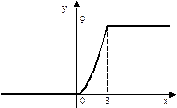
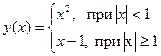 , е)
, е) 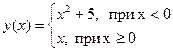



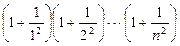 ;
;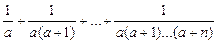 ;
;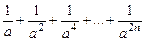 .
.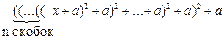 .
.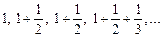 первое, большее a;
первое, большее a;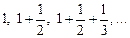 первое, меньшее a;
первое, меньшее a;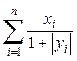 .
.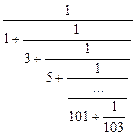 .
.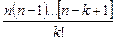 .
.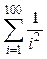 ; б)
; б) 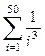 ; в)
; в) 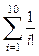 ; г)
; г) 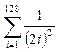 ; д)
; д) 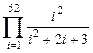 ;
;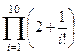 ; ж)
; ж) 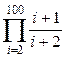 ; з)
; з) 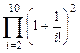 и)
и) 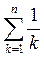 ; к)
; к) 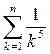 ;
; 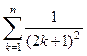 ; м)
; м) 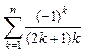 ; н)
; н) 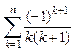 ; о)
; о) 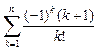 ; п)
; п)  .
.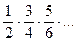 ; б)
; б) 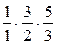 .
.


