
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистические распределения.Содержание книги Поиск на нашем сайте
Микроскопические параметры. Вероятность и флуктуации. Распределение Максвелла. Средняя кинетическая энергия частицы. Скорости теплового движения частиц. Распределение Больцмана. Функции распределения Бозе и Ферми. Теплоемкость многоатомных газов. Недостаточность классической теории теплоемкости. Модель системы в термостате. Понятие о каноническом распределении Гиббса. Статистический смысл термодинамических потенциалов и температуры. Роль свободной энергии. Распределение Гиббса для системы с переменным числом частиц.
Элементы физической кинетики. Релаксационные явления. Время релаксации различных процессов приближения к тепловому равновесию. Броуновское движение. Связь диффузии с броуновским движением. Понятие о принципе Онзагера, о перекрестных эффектах. Диффузия и теплопроводность. Коэффициент диффузии и теплопроводности. Время выравнивания. Диффузия в газах и в твердых телах. Вязкость. Коэффициент вязкости газов и жидкостей. Динамическая и кинетическая вязкости.
Фазовые равновесия и фазовые превращения. Реальные газы. Силы и потенциальная энергия межмолекулярного взаимодействия. Уравнение Ван-дер-Ваальса. Фазы и фазовые превращения. Условие равновесия фаз. Фазовые диаграммы. Уравнение Клапейрона-Клаузиуса. Критическая точка. Метастабильные состояния. Тройная точка. Фазовые переходы второго рода. Особенности жидкого и твердого состояний вещества.
Порядок и беспорядок в природе. Энтропия как количественная мера хаотичности. Переход от порядка к беспорядку в состоянии теплового равновесия. Ближний и дальний порядок. Координационный и ориентационный порядки. Жидкие кристаллы. Структурное упорядочение кристаллов. Понятие о магнитном порядке. Неупорядоченные макросистемы. Открытые диссипативные системы. Появление самоорганизации в открытых системах и превращение флуктуаций в макроскопические эффекты. Понятие о бифуркациях. Идеи синергетики. Периодические химические реакции и биоритмы. Концептуальные уровни в познании веществ и химические системы. Химические процессы, самоорганизация и эволюция химических систем.
Вопросы для контроля знаний и выполнения учебной проектной работы
1. Укажите некоторые экспериментальные факты, подтверждающие положения молекулярно-кинетической теории. 2. Какие реальные процессы можно считать равновесными (примеры)? 3. Опишите законы идеальных газов для изопроцессов и дайте их графическую интерпретацию. 4. Сформулируйте закон Дальтона для смеси газов. 5. Приведите различные формы записи основного уравнения молекулярно-кинетической теории. В чем его основное содержание? 6. Сформулируйте закон классической статистической физики о равномерном распределении энергии по степеням свободы молекулы. 7. Как определяется средняя энергия молекул газа известной температуры? 8. У какого из газов (кислород О2, углекислый газ СО2, азот N2 и гелий Не) при одинаковой температуре средняя кинетическая энергия молекул наибольшая? 9. Как определяется внутренняя энергия 1 моля идеального газа и любой массы этого газа? 10. Укажите процесс, в котором изменение внутренней энергии равно нулю. 11. Какая задача решается Максвеллом при определении скорости молекул, в виду полной беспорядочности движения огромного их числа? 12. Какие физические величины определяют вид функции распределения Максвелла? Каков физический смысл этой функции? 13. Что определяет вся площадь под кривой распределения Максвелла и отдельные участки этой площади? 14. Охарактеризуйте три скорости, определяющие усредненное движение всей совокупности молекул и сравните их: среднюю арифметическую < v >, среднюю квадратичную < v кв> и наиболее вероятную < v в> скорости. Покажите как определяются эти скорости с помощью функции распределения F (v). 15. Охарактеризуйте распределение Максвелла как равновесное распределение; при каких условиях оно выполняется? Какие квантовые статистики Вы знаете и какова их краткая характеристика? 16. В каких условиях находится газ, составляющий атмосферу Земли? 17. Как влияет изменение температуры и природы газа на закон изменения давления с высотой? 18. Как изменяется концентрация молекул с высотой? Как распределились бы молекулы по высоте при температуре абсолютного нуля (Т ® 0) и при очень больших температурах? 19. Определите, используя распределение Больцмана, долю частиц, которые в условиях теплового равновесия обладают определенной потенциальной энергией U (x, y, z). Как зависит распределение частиц по энергиям от температуры?
20. Дайте определение средней длины свободного пробега молекул < l > и среднего числа столкновений молекул < Z > в единицу времени. Как влияют эти величины на явления переноса? 21. Укажите известные Вам явления переноса. В чем их общность (условие, причины, результат)? 22. Охарактеризуйте явление внутреннего трения (вязкость). 23. Охарактеризуйте равновесный процесс; приведите примеры реальных процессов, близких к равновесным. 24. Дайте определение прямого и обратного кругового процесса (цикла), отобразите его на диаграмме состояния; охарактеризуйте использование круговых процессов в тепловых машинах (различных типов). 25. Какие виды теплообмена Вы знаете и каков механизм процессов теплообмена? 26. Каково условие равновесного состояния газа во внешнем поле силы тяжести? 27. Сформулируйте и запишите первый закон термодинамики. За счет чего совершается работа системой в случае, если совершаемая работа больше количества теплоты, получаемой системой? 28. Охарактеризуйте (с использованием простейшей схемы) работу тепловой машины на примере идеализированной паровой машины (рабочее вещество – вода и пар). 29. Дайте формулировку I начала термодинамики, связанную с работой тепловых двигателей. 30. Определите коэффициент полезного действия (КПД) тепловой машины. 31. Охарактеризуйте работу холодильной машины. Определите ее эффективность через холодильный коэффициент. 32. Дайте определение теплоемкости С. Что влияет на величину теплоемкости и в каких единицах она измеряется? 33. Дайте определение удельной и молярной теплоемкости однородных тел и установите соотношение между ними. 34. Определите молярные теплоемкости при постоянном объеме и при постоянной давлении, а также их отношение, используя число степеней свободы молекулы. 35. Рассмотрите условия, при которых закон квантования энергии вращения и колебаний молекул переходит в классический закон равнораспределения энергии по степеням свободы. 36. Как практически осуществляются адиабатические процессы? Получите уравнение адиабаты для параметров состояния газа Р (давление) и V (объем). 37. Обобщите и охарактеризуйте процессы изменения состояния газа как политропические процессы. Какое условие выполняется в ходе политропического процесса? 38. Как можно определить работу, совершаемую каким-либо телом над внешними телами в произвольном процессе и при адиабатическом переходе из состояния 1 в состояние 2? 39. Приведите необходимое и достаточное условие обратимости процесса. Почему все реальные процессы необратимы? 40. Изложите содержание II-го начала термодинамики в формулировке Кельвина-Планка. 41. Дайте общую характеристику цикла Карно. Из каких процессов состоит этот круговой процесс? Отобразите прямой цикл Карно на диаграмме P - V для идеального газа. Как определяется КПД цикла Карно? 42. Дайте определение приведенного количества теплоты Q *. Как определить Q * в изотермическом процессе (при нагревании и при охлаждении тела) и в произвольном процессе? 43. Сделайте вывод об изменении энтропии замкнутой системы при любом элементарном процессе изменения ее состояния. 44. Определите значение термодинамической вероятности Р и энтропии S для абсолютно упорядоченного движения.
45. Как можно трактовать понятие «энтропия», согласно известного соотношения Л. Больцмана S = k ln W, где k = const? 46. Охарактеризуйте модель газа Ван-дер-Ваальса – реального газа. Каков смысл поправок при выводе уравнения Ван-дер-Ваальса? Запишите уравнение Ван-дер-Ваальса для 1 моля газа. 47. Изобразите экспериментальные изотермы реальных газов (влажный пар) для различных температур. Охарактеризуйте критическое состояние вещества. Рассмотрите на примере одной из до критических изотерм, какие участки кривой соответствуют различным агрегатным состояниям вещества? 48. Выделите на рисунке с изотермами реальных газов для различных температур колоколообразную кривую, которая ограничивает область двухфазных состояний вещества. Какие области выделяет эта кривая и участки критической изотермы? Покажите пограничную кривую кипения и пограничную кривую конденсации. Каким фазовым переходам они соответствуют? 49. Чем отличается фазовый переход I рода от фазового перехода II рода? 50. Объясните положительный и отрицательный эффект Джоуля-Томсона (адиабатическое дросселирование); изобразите принципиальную схему опытов Д. Джоуля и В. Томсона.
Основные формулы (Молекулярная физика и термодинамика)
1. 2. 3. 4. 5. Р = Р 1 + Р 2 + … + РК – закон Дальтона, где Р – давление смеси газов; Р i – парциальное давление i -го компонента смеси. 6. 7. 8. Средняя кинетическая энергия:
9. Р = nkT – зависимость давления газа от концентрации n и температуры Т. 10. Скорость молекул:
11.
12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. С m = cM – связь между молярной С m и удельной c теплоемкостями газа. 24. 25. 26. СР – С V = R – уравнение Майера. 27. 28. U = n CVT = 29. 30. А = Р (V 2 – V 1) – работа газа при Р = const. 31. 32. 33. PV g = const – уравнение Пуассона. 34. 35. d Q = dU + d A – первое начало термодинамики. 36. 37. 38. 39. 40. 41. 42. 43. 44. 45. 46. Vm кр = 3 b;
Основные типы задач индивидуального задания №2 связаны со следующими теоретическими вопросами учебной программы: – Молекулярно–кинетическая трактовка (МКТ) давления. – Кинетическая энергия хаотического движения молекул. Скорости молекул. – Основное уравнение МКТ. – Закон распределения Максвелла по величине скорости молекул. – Закон распределения Больцмана.
– Первое начало термодинамики и его применение к изопроцессам (использование дифференциальной формы записи первого начала термодинамики целесообразно только в тех случаях, когда с помощью этого закона и уравнения состояния нужно найти уравнения процесса или теплоемкость газа). – Стандартные задачи на распределения Максвелла или Больцмана сводятся к определению средних физических величин и к нахождению числа частиц, обладающих некоторым свойством. – Основная задача термодинамики равновесных процессов заключается в нахождении всех макросостояний системы. Если начальное и конечное состояния системы известны, то можно определить изменение ее внутренней энергии (при этом часто используют еще и уравнение Клапейрона-Менделеева) – Если, кроме того, известны и промежуточные состояния системы (например, известен процесс), то можно найти работу, совершенную системой, рассчитать полученное или отданное системой количество теплоты. – Задачи этого раздела зачастую имеют расчетный характер, поэтому важно проанализировать полученный численный ответ. Примеры решения задач ИДЗ №2
Задача 1. Найдите число молекул водорода в 1 см3, если давление равно 200 мм.рт.ст., а средняя квадратичная скорость молекул при данных условиях 2400 м/с. Решение
Отсюда температура
Задача 2. Средняя квадратичная скорость молекулы углекислого газа при давлении Р = 105 Па равна 628 м/с. Определите среднюю длину свободного пробега молекул <l>. Решение
Учтем, что
Задача 3. Найдите число атомов в молекуле газа, у которого при «замораживании» колебательных степеней свободы постоянная g увеличивается в 1,2 раза. Решение
Число поступательных степеней свободы i пост = 3, а число вращательных степеней свободы i вр и число колебательных степеней свободы i кол зависит от пространственного строения рассматриваемой молекулы. Если молекула имеет линейную структуру (все атомы в молекуле соединены в виде прямолинейной цепочки), то i вр = 2; i кол = 3 N – (i пост + i вр) = 3 N – 5. Если же молекула имеет «объемную» структуру, то i вр = 3; i кол = 3 N – 6. Рассмотрим эти два случая. До «замораживания» колебательных степеней свободы число i равно сумме 3 + 2 + 2(3 N – 5) = 6 N – 5, а после «замораживания» (при достаточно низких температурах газа) 3 + 2 = 5. По условию задачи «замораживание» колебательных степеней свободы приводит к возрастанию g в k = 1,2 раза, поэтому Итак, число атомов в молекуле равно четырем; молекула имеет нелинейную структуру.
Задача 4. Высокий цилиндрический сосуд с азотом находится в однородном поле тяжести, ускорение свободного падения в котором равно g. Температура азота меняется по высоте так, что его плотность всюду одинакова. Найдите градиент температуры dT / dh.
Решение
Задача 5. Найдите наиболее вероятную скорость молекул идеального газа. Решение
Введем обозначение:
Чтобы найти наиболее вероятную скорость, нужно взять производную этой функции по скорости и приравнять ее к нулю.
f ¢(v в) = 0; это возможно при
Задача 6. Найдите наиболее вероятную энергию молекул идеального газа. Решение
Определим точку максимума функции распределения молекул идеального газа по энергиям:
Производная этой функции по Е равна
Искомую энергию Е в найдем из условия f ¢(Е) = 0, то есть
Задача 7. Водород находится при нормальных условиях и занимает объем 1 см3. Определите число D N молекул в этом объеме, обладающих скоростями, меньшими некоторого значения v max = 1 м/с. Решение
Для решения задачи, удобно воспользоваться распределением молекул по относительным скоростям
Из (2) Для таких значений u выражение (3) можно существенно упростить. Для u << 1 имеем
Общее число молекул: Из уравнения Менделеева-Клапейрона
Подставив (6) в (5), получим
Задача 8. Пусть проводятся наблюдения за частицами, имеющими форму шарика и находящимися во взвешенном состоянии в воздухе, в поле земного тяготения. Радиус частиц r = 2×10-7 м. Температура воздуха t = 0 °С, давление Р = 105 Па. Установлено, что на высоте h = 10 м концентрация частиц уменьшается в 2 раза. Найдите массу m 0 взвешенной частицы. Решение
Плотность частицы равна
m = 5,4×10-21 кг.
Задача 9. Внутренняя энергия некоторой массы кислорода равна 3500 Дж. Определите суммарную кинетическую энергию W поступательного движения молекул газа. Решение
где i – число степеней свободы. Суммарная кинетическая энергия поступательного движения для N молекул определяется как
где kNA = R. Из уравнения (1) находим
Задача 10. Баллон емкостью V 1 = 10 л с кислородом, имевшим температуру t 1 = 7 ° С при давлении Р = 8 МПа, нагревается до t 2 = 15.5 °С. Какое количество теплоты D Q при этом поглощает газ?
Решение
Применим к первоначальному состоянию уравнение Менделеева-Клапейрона:
Задача 11. Некоторую массу m идеального газа с молярной массой М нагревают под поршнем так, что температура изменяется пропорционально квадрату давления от первоначального значения Т 1 до Т 2. Определите работу, совершенную газом. Решение
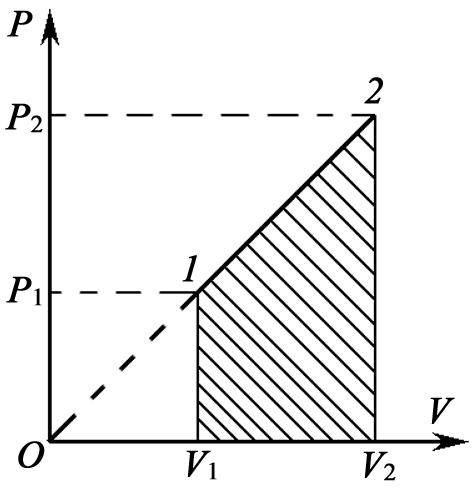
т.е. в ходе процесса давление и объем связаны прямой пропорциональной зависимостью. При этом работа газа равна площади заштрихованной трапеции, т.е.
где Р 1 и V 1 – начальные, а Р 2 и V 2 – конечные давление и объем. Так как прямая 1 – 2 проходит через начало координат, то
Тогда Из уравнения Менделеева-Клапейрона для первого и второго состояний газа можно получить:
Итак, работа, совершенная газом, равна
Решение
Работа, совершенная газом по изобаре 3 – 1: А 3–1 = - А ¢3–1 = -3n RT 1. Работа газа за цикл А ц = А 1–2 + А 2–3 + А 3–1. На участке 1 – 2 работа численно равна площади трапеции, в которой этот участок является одной из боковых сторон:
По условию прямая 1 – 2 проходит через начало координат, поэтому справедливо соотношение
Работа газа на участке 2 – 3 численно равна площади трапеции, у которой этот участок является одной из боковых сторон:
По условию Р 2 V 2 = P 3 V 3
Окончательно получаем для искомой величины:
Задача 13. Температуру газа, имеющую массу m и молярную массу М, повышают на величину D Т один раз при постоянном давлении Р, а другой раз при постоянном объеме V. Насколько отличаются сообщенные газу количества теплоты QP и QV и удельные теплоемкости cP и cV при постоянном давлении и постоянном объеме? Решение
Запишем уравнения состояния газа до и после нагревания:
Вычитая из (4) уравнение (3), получаем
В результате
При постоянном объеме работа расширения газа А = 0. Первое начало термодинамики выглядит так: QV = D U. (7) Вычитая из
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 167; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.69.216 (0.011 с.) |

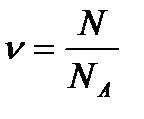 – число молей вещества, где N – число структурных элементов, составляющих систему; N А – постоянная Авогадро.
– число молей вещества, где N – число структурных элементов, составляющих систему; N А – постоянная Авогадро.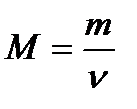 – молярная масса вещества, где m – масса системы.
– молярная масса вещества, где m – масса системы.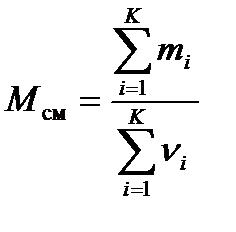 – молярная масса смеси газов, где mi – масса i -го компонента смеси; n i – количество вещества i -го компонента смеси; K – число компонентов смеси.
– молярная масса смеси газов, где mi – масса i -го компонента смеси; n i – количество вещества i -го компонента смеси; K – число компонентов смеси.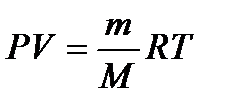 – уравнение Клапейрона-Менделеева.
– уравнение Клапейрона-Менделеева.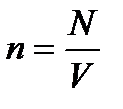 – концентрация частиц однородной системы, где V – объем системы.
– концентрация частиц однородной системы, где V – объем системы.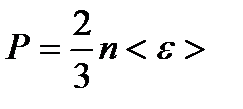 – основное уравнение МКТ, где <e> - средняя кинетическая энергия поступательного движения молекулы.
– основное уравнение МКТ, где <e> - средняя кинетическая энергия поступательного движения молекулы.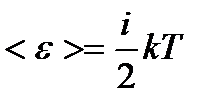 – приходящегося на все степени свободы i молекулы;
– приходящегося на все степени свободы i молекулы;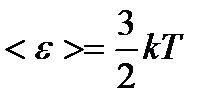 – поступательного движения молекулы;
– поступательного движения молекулы;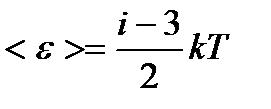 – вращательного движения молекулы;
– вращательного движения молекулы;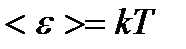 – колебательного движения молекулы, где k – постоянная Больцмана.
– колебательного движения молекулы, где k – постоянная Больцмана.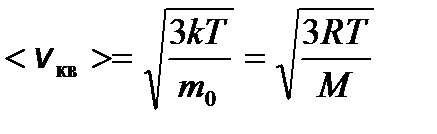 – средняя квадратичная;
– средняя квадратичная;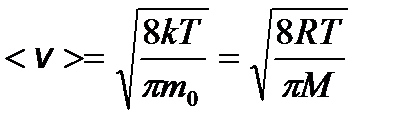 – средняя арифметическая;
– средняя арифметическая;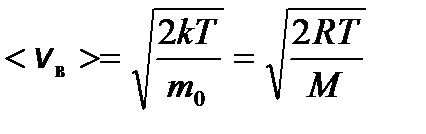 – наиболее вероятная, где m 0 – масса одной молекулы.
– наиболее вероятная, где m 0 – масса одной молекулы.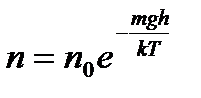 – распределение Больцмана, где n – концентрация частиц в точках поля, где потенциальная энергия их равна mgh; n 0 – концентрация частиц, где mgh = 0.
– распределение Больцмана, где n – концентрация частиц в точках поля, где потенциальная энергия их равна mgh; n 0 – концентрация частиц, где mgh = 0.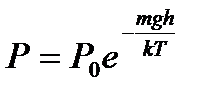 – барометрическая формула, где Р 0 – давление газа на уровне, принятому за нулевой.
– барометрическая формула, где Р 0 – давление газа на уровне, принятому за нулевой.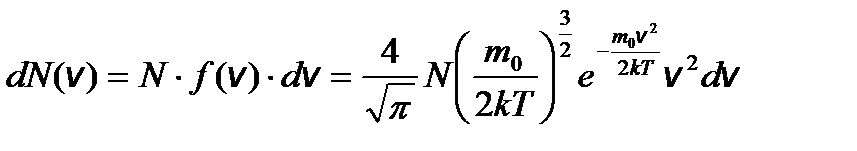 – распределение Максвелла (распределение молекул по скоростям).
– распределение Максвелла (распределение молекул по скоростям).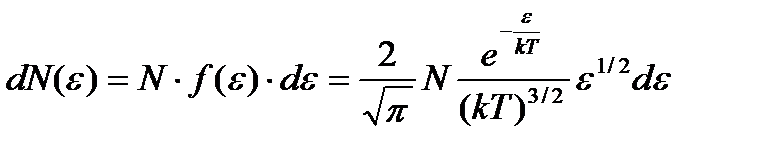 – распределение молекул по кинетическим энергиям поступательного движения.
– распределение молекул по кинетическим энергиям поступательного движения.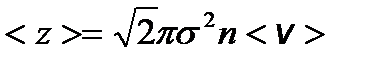 – среднее число соударений, испытываемых одной молекулой газа в единицу времени, где s - эффективный диаметр молекулы.
– среднее число соударений, испытываемых одной молекулой газа в единицу времени, где s - эффективный диаметр молекулы.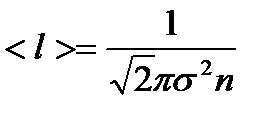 – средняя длина свободного пробега молекул.
– средняя длина свободного пробега молекул.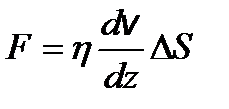 – закон Ньютона, где F – сила внутреннего трения между движущимися слоями газа;
– закон Ньютона, где F – сила внутреннего трения между движущимися слоями газа; 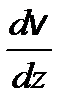 – градиент скорости; D S – площадь элемента поверхности.
– градиент скорости; D S – площадь элемента поверхности.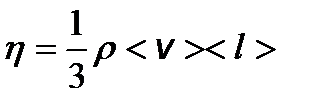 – динамическая вязкость, где r - плотность газа (жидкости).
– динамическая вязкость, где r - плотность газа (жидкости).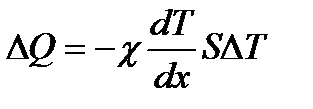 – закон Фурье, где D Q – теплота, прошедшая посредством теплопроводности через сечение площадью S за время D t; c - коэффициент теплопроводности;
– закон Фурье, где D Q – теплота, прошедшая посредством теплопроводности через сечение площадью S за время D t; c - коэффициент теплопроводности; 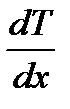 – градиент температуры.
– градиент температуры.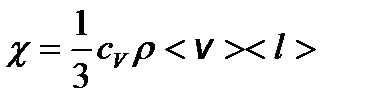 – коэффициент теплопроводности, где cV – удельная теплоемкость газа при постоянном объеме.
– коэффициент теплопроводности, где cV – удельная теплоемкость газа при постоянном объеме.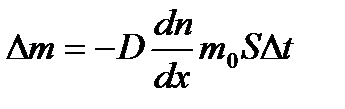 – закон Фика, где D m – масса газа, перенесенная в результате диффузии через поверхность площадью S за время D t; D – коэффициент диффузии;
– закон Фика, где D m – масса газа, перенесенная в результате диффузии через поверхность площадью S за время D t; D – коэффициент диффузии; 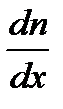 – градиент концентрации молекул; m 0 – масса одной молекулы.
– градиент концентрации молекул; m 0 – масса одной молекулы.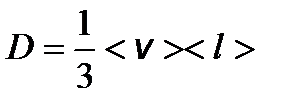 – коэффициент диффузии.
– коэффициент диффузии.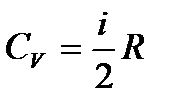 – молярная теплоемкость при постоянном объеме.
– молярная теплоемкость при постоянном объеме.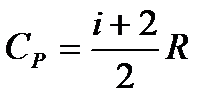 – молярная теплоемкость при постоянном давлении.
– молярная теплоемкость при постоянном давлении.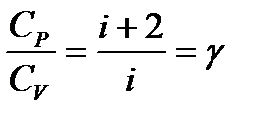 – показатель адиабаты.
– показатель адиабаты.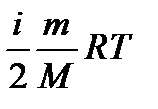 – внутренняя энергия идеального газа.
– внутренняя энергия идеального газа.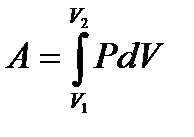 – работа, совершаемая газом при изменении его объема.
– работа, совершаемая газом при изменении его объема.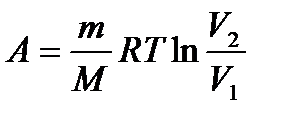 – работа газа при Т = const.
– работа газа при Т = const.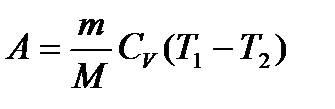 или
или 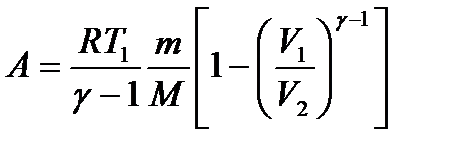 – работа при адиабатическом процессе.
– работа при адиабатическом процессе.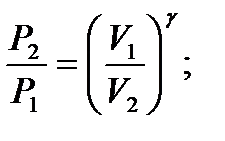
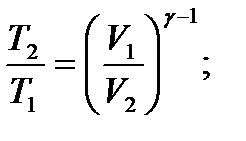
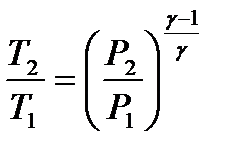 – связь между начальным и конечным значениями параметров состояний газа при адиабатическом процессе.
– связь между начальным и конечным значениями параметров состояний газа при адиабатическом процессе.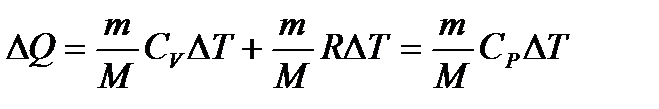 – первое начало термодинамики при изобарном процессе.
– первое начало термодинамики при изобарном процессе.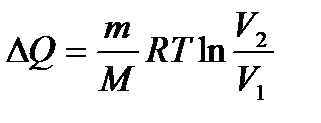 – первое начало термодинамики при изотермическом процессе.
– первое начало термодинамики при изотермическом процессе.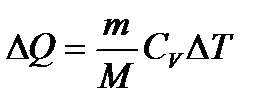 – первое начало термодинамики при изохорном процессе.
– первое начало термодинамики при изохорном процессе.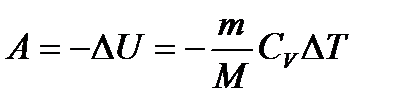 – первое начало термодинамики при адиабатическом процессе.
– первое начало термодинамики при адиабатическом процессе.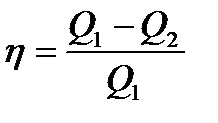 или
или 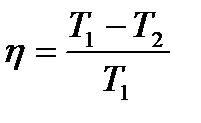 к.п.д. цикла Карно.
к.п.д. цикла Карно.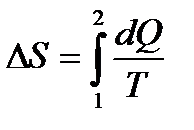 – изменение энтропии S системы.
– изменение энтропии S системы.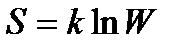 – формула Больцмана, где W – термодинамическая вероятность состояния системы; k – постоянная Больцмана.
– формула Больцмана, где W – термодинамическая вероятность состояния системы; k – постоянная Больцмана.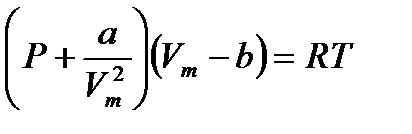 – уравнение Ван-дер-Ваальса для одного моля газа, где Vm – молярный объем; а и b – постоянные, рассчитанные на один моль газа; P – давление газа на стенки сосуда.
– уравнение Ван-дер-Ваальса для одного моля газа, где Vm – молярный объем; а и b – постоянные, рассчитанные на один моль газа; P – давление газа на стенки сосуда.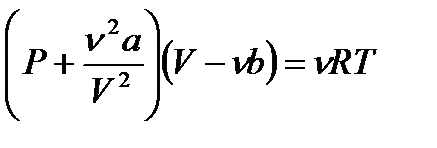 – уравнение Ван-дер-Ваальса для произвольного количества вещества n газа; V – объем занимаемый газом.
– уравнение Ван-дер-Ваальса для произвольного количества вещества n газа; V – объем занимаемый газом.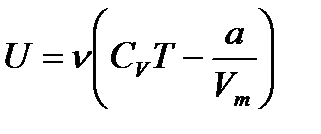 – внутренняя энергия реального газа.
– внутренняя энергия реального газа.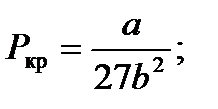
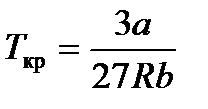 связь критических параметров – объема, давления и температуры газа – с постоянными а и b Ван-дер-Ваальса.
связь критических параметров – объема, давления и температуры газа – с постоянными а и b Ван-дер-Ваальса.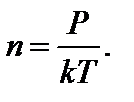
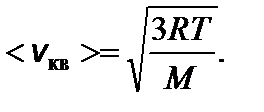
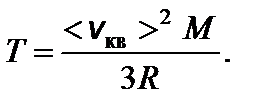 Окончательно получаем выражение для n
Окончательно получаем выражение для n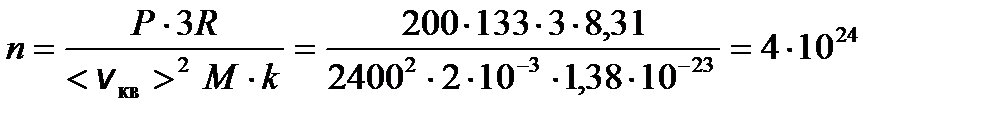 1/м3.
1/м3.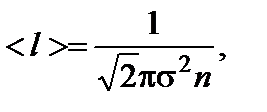 где s - эффективный диаметр молекул; n – концентрация
где s - эффективный диаметр молекул; n – концентрация 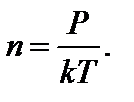
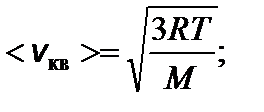
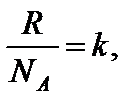 тогда
тогда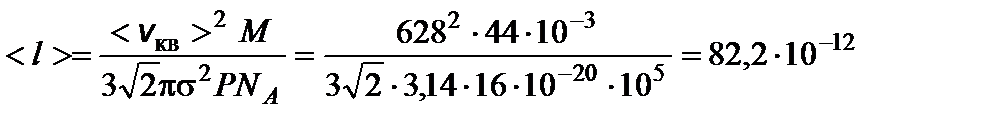 м = 82,2 пм.
м = 82,2 пм.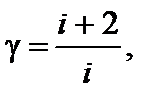 где число степеней свободы i = i пост + i вр + 2 i кол.
где число степеней свободы i = i пост + i вр + 2 i кол.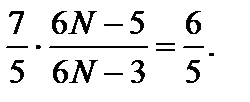 Отсюда N = 17/6. Это число не является целым и, следовательно, рассматриваемая молекула не может иметь линейную структуру. В этом случае уравнение для определения числа атомов N в молекуле имеет вид
Отсюда N = 17/6. Это число не является целым и, следовательно, рассматриваемая молекула не может иметь линейную структуру. В этом случае уравнение для определения числа атомов N в молекуле имеет вид 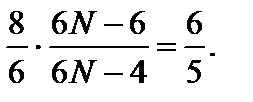 Отсюда N = 4.
Отсюда N = 4.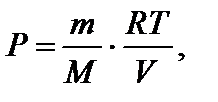 где М – молярная масса газа.
где М – молярная масса газа.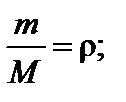
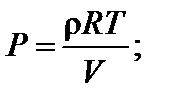

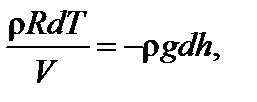 откуда искомая величина равна
откуда искомая величина равна 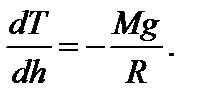
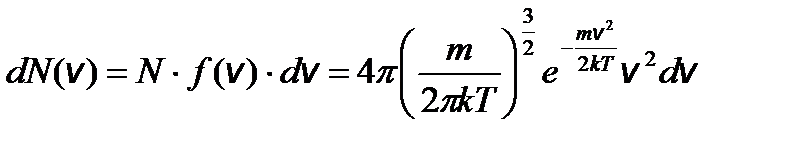 .
.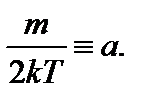 Тогда функция распределения молекул по абсолютным значениям скорости будет иметь вид:
Тогда функция распределения молекул по абсолютным значениям скорости будет иметь вид: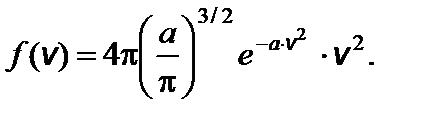
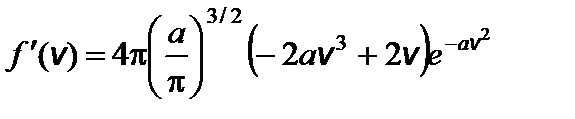
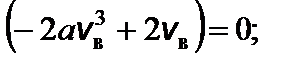
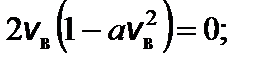
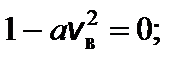
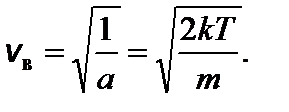

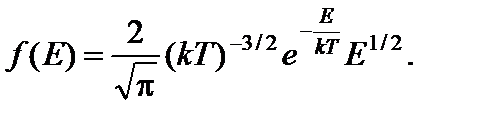
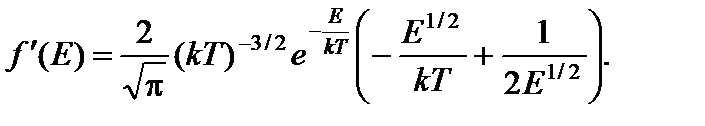
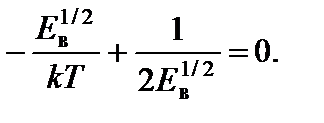 Отсюда следует
Отсюда следует 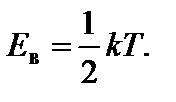
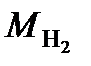 = 2×10-3 кг/моль
R = 8,31 Дж/моль×К
= 2×10-3 кг/моль
R = 8,31 Дж/моль×К
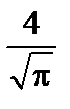 N А 3/2
N А 3/2 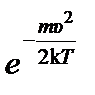 v 2 d v. (1)
v 2 d v. (1)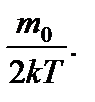
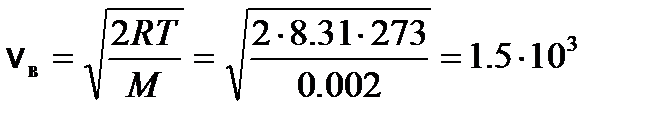 м/с
м/с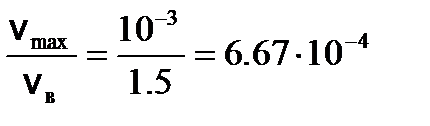 (v max << v в) (2)
(v max << v в) (2)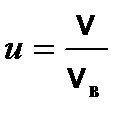 . Согласно (1) и соотношению
. Согласно (1) и соотношению 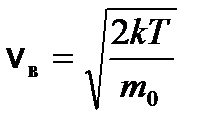 , число dN (u) молекул, относительные скорости u которых заключены в интервале от u до u + du, определяется формулой
, число dN (u) молекул, относительные скорости u которых заключены в интервале от u до u + du, определяется формулой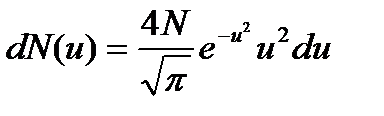 . (3)
. (3)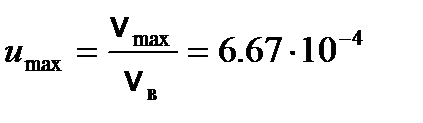 .
.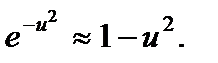 Пренебрегая значением u 2» 44.5×10-8, по сравнению с единицей, запишем выражение (3) в виде
Пренебрегая значением u 2» 44.5×10-8, по сравнению с единицей, запишем выражение (3) в виде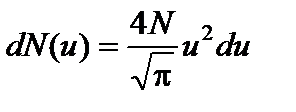 .
.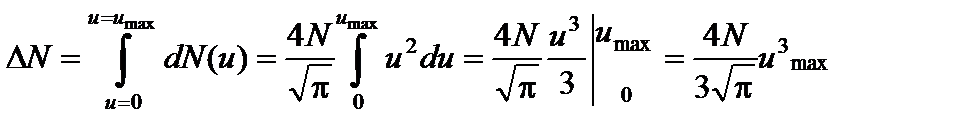 . (4)
. (4)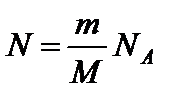 , (здесь m – масса газа). (5)
, (здесь m – масса газа). (5)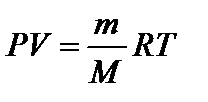 имеем
имеем 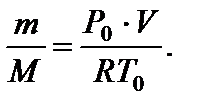 (6)
(6)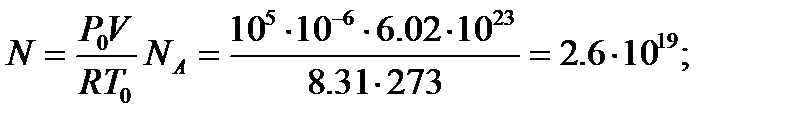
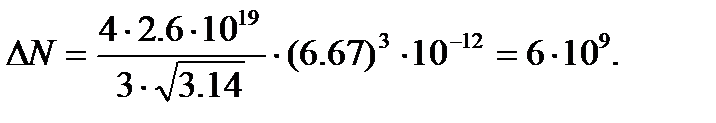
 . Обозначим массу частицы m. Сила, действующая на частицу, равна
. Обозначим массу частицы m. Сила, действующая на частицу, равна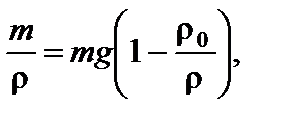
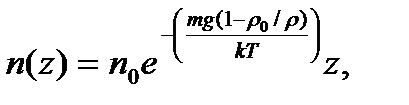
 где z – координата точки (высота) по отношению к уровню, принятому за нулевой (уровень Земли).
где z – координата точки (высота) по отношению к уровню, принятому за нулевой (уровень Земли).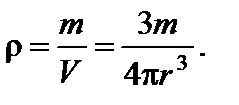 Отношение концентраций частиц на двух различных высотах по условию равно 2, тогда
Отношение концентраций частиц на двух различных высотах по условию равно 2, тогда 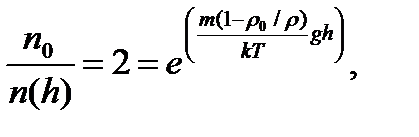 откуда
откуда 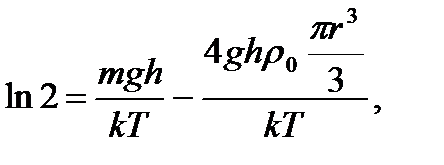
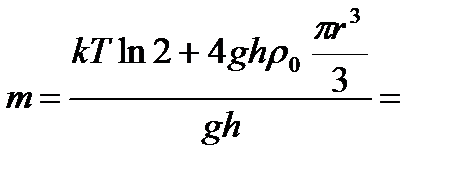
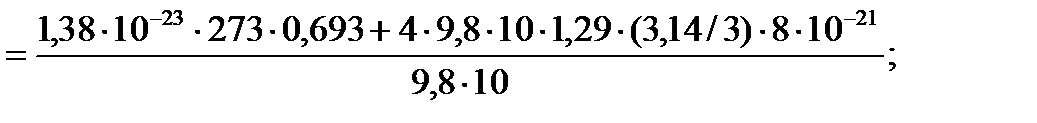
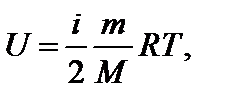 (1)
(1)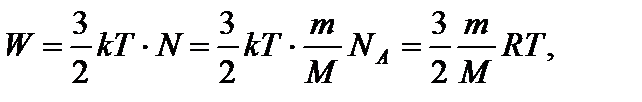 (2)
(2)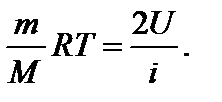 Тогда
Тогда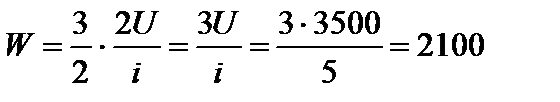 Дж.
Дж.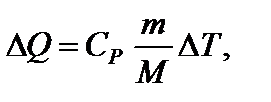
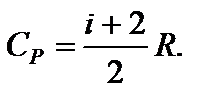
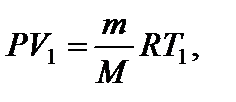 откуда
откуда 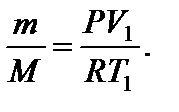 Искомое количество теплоты равно
Искомое количество теплоты равно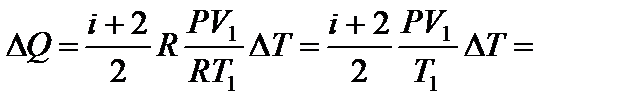
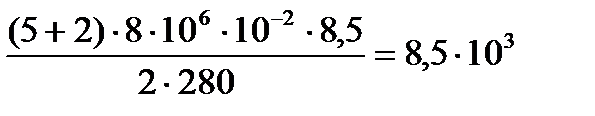 Дж.
Дж.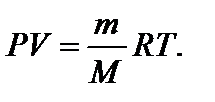
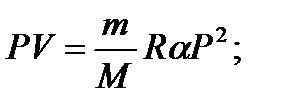
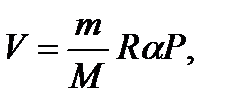
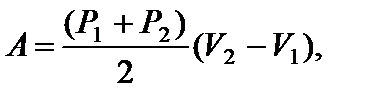
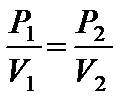 или Р 1 V 2 = P 2 V 1.
или Р 1 V 2 = P 2 V 1.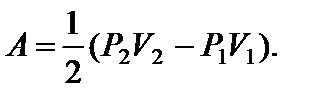
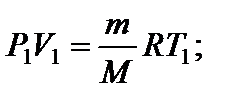
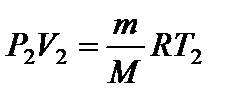
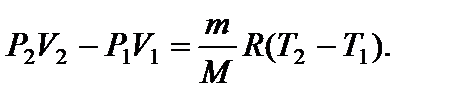
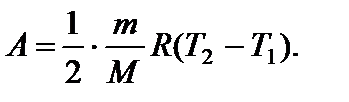
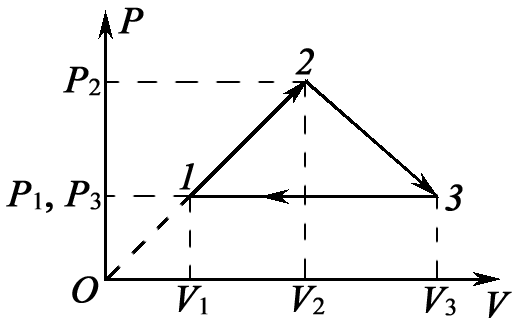 Задача 12. На рисунке для n молей гелия показан цикл, состоящий из двух участков линейной зависимости давления Р от объема V и изобары. На изобаре 3 – 1 над газом совершили работу А ¢3–1 (А ¢3–1 > 0) и его температура уменьшилась в 4 раза. Температуры в состояниях 2 и 3 равны. Точки 1 и 2 на диаграмме Р – V лежат на прямой, проходящей через начало координат. Определите температуру Т 1 в точке 1. Найдите работу газа за цикл.
Задача 12. На рисунке для n молей гелия показан цикл, состоящий из двух участков линейной зависимости давления Р от объема V и изобары. На изобаре 3 – 1 над газом совершили работу А ¢3–1 (А ¢3–1 > 0) и его температура уменьшилась в 4 раза. Температуры в состояниях 2 и 3 равны. Точки 1 и 2 на диаграмме Р – V лежат на прямой, проходящей через начало координат. Определите температуру Т 1 в точке 1. Найдите работу газа за цикл.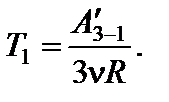
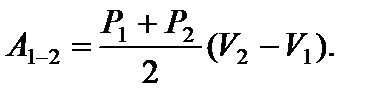
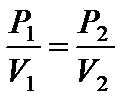 и тогда
и тогда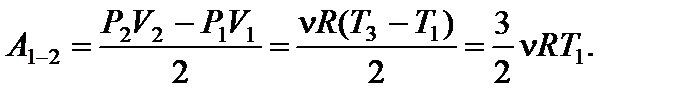
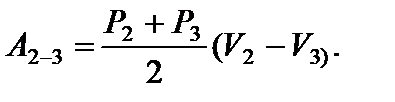
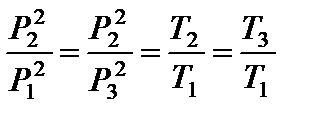
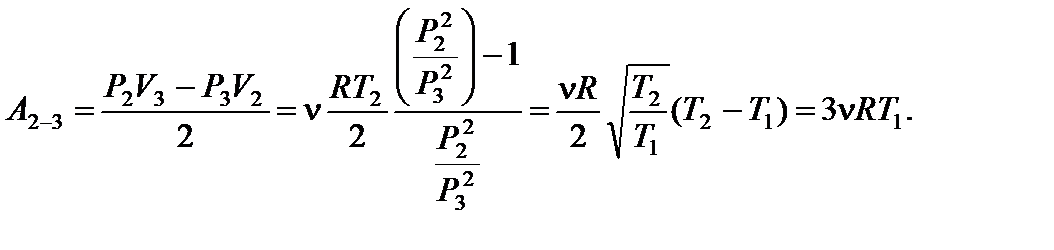
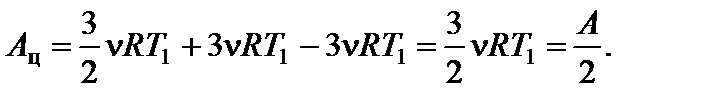
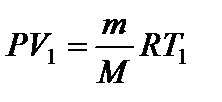 (3)
(3)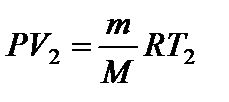 (4)
(4)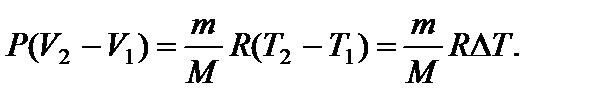 (5)
(5)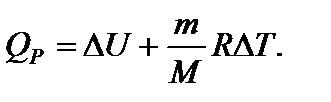 (6)
(6)


