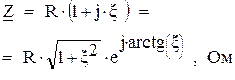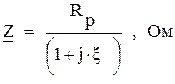Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пояснения к изучаемым вопросам. Эти вопросы удобнее всего изучать по [1,3,5,8,9]Содержание книги
Поиск на нашем сайте
Эти вопросы удобнее всего изучать по [1,3,5,8,9]. Особое внимание необходимо уделить приобретению навыка в решении задач. При изучении этих вопросов следует обратить внимание на различие в форме записи амплитуд Um, Im, Em и действующих значений – U, I, E. Соотношение между амплитудой и действующим значением:
Функция мгновенных значений физической величины (например, напряжения), изменяющаяся по закону гармонической функции, изображается в виде функции комплексной амплитуды (или комплексного действующего значения):
Любое комплексное число может быть изображено в виде вектора на комплексной плоскости (рисунки 2.4, 2.5). Основные формы записи комплексных чисел показаны в таблице 2.1.
Таблица 2.1
Основные правила вычислений с использованием комплексных чисел: Представление мнимой единицы:
Если заданы два комплексных числа, представленные в алгебраической или показательной формах:
их алгебраическая сумма: произведение: частное от деления: корень степени “n”: Следует обратить внимание на особенности перевода комплексного числа из алгебраической формы в показательную в случае, если действительная часть комплексного числа отрицательная. Рассмотрим примеры преобразований.
Требуется представить комплексное число
Пример 2: Число
Методы расчёта цепей в режиме гармонических колебаний те же, что и для цепей постоянного тока, но в расчётах используются изображения гармонических функций в виде комплексных амплитуд (или комплексных действующих значений). Основные соотношения сведены в таблицу 2.2.
Таблица 2.2.
2.4. Частотные характеристики электрических цепей.
Основные изучаемые вопросы
1. RLC – цепи при гармоническом воздействии. Входные и передаточные характеристики. Амплитудно-частотные и фазочастотные характеристики. 2. Последовательный контур. Явление резонанса. Понятия: расстройка, полоса пропускания, добротность, избирательность контура. Влияние сопротивления нагрузки на характеристики контура. 3. Параллельный контур. Влияние внутреннего сопротивления генератора и сопротивления нагрузки на характеристики контура.
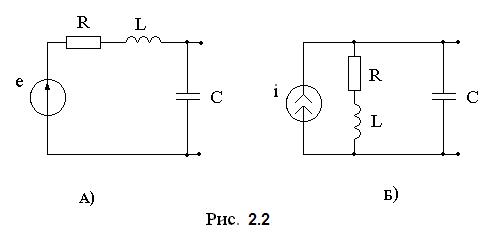
Пояснения к изучаемым вопросам Эти вопросы удобнее всего изучать по [1, 3, 9]. Явление резонанса наблюдается в RLC – контурах, когда частота источника гармонических колебаний на входе цепи совпадает с резонансной частотой контура. На рисунке 2.2 представлены схемы простейших ненагруженных контуров с малыми потерями.
Последовательный контур (рис. 2.2.А) будет настроен в резонанс при частоте, на которой мнимая часть входного сопротивления будет равна нулю:
Параллельный контур (рис. 2.2.Б) будет настроен в резонанс при частоте, на которой мнимая часть входной проводимости будет равна нулю:
При условии, что потери очень малы: Необходимо знать следующие основные определения и соотношения:
2.5. Спектральное представление сигналов.
Основные изучаемые вопросы 1. Понятия: негармонический периодический сигнал, тригонометрическая форма ряда Фурье, комплексная форма ряда Фурье, линейчатый амплитудный спектр, линейчатый фазовый спектр, действующее значение периодического негармонического сигнала, среднее значение периодического негармонического сигнала, средняя активная мощность периодического негармонического сигнала, равенство Парсеваля.
2.Понятия: непериодический сигнал (одиночный импульс), прямое и обратное преобразования Фурье, комплексная спектральная плотность, амплитудный спектр (спектральная плотность амплитуд), фазовый спектр, энергия непериодического сигнала, спектральная плотность энергии непериодического сигнала.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-26; просмотров: 49; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.66.195 (0.007 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 .
.

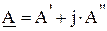
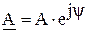


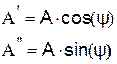
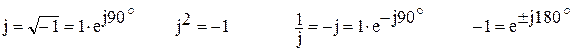
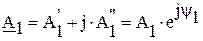 и
и  , то
, то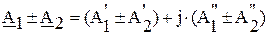
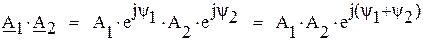

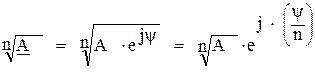
 Пример 1:
Пример 1: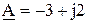 (рис.2.4) в показательной форме:
(рис.2.4) в показательной форме:
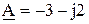 (рис.2.5) требуется представить в показательной форме:
(рис.2.5) требуется представить в показательной форме:

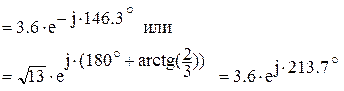 .
.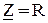
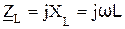
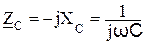
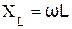
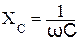
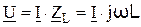
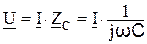
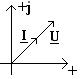
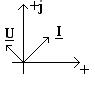
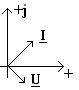
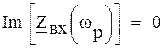 , то есть при
, то есть при 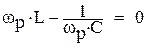 , откуда
, откуда 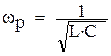
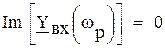 , то есть при
, то есть при 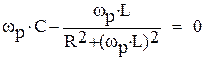 , откуда
, откуда 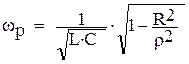 , где
, где 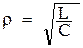 - характеристическое сопротивление.
- характеристическое сопротивление.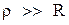 , можно принять
, можно принять 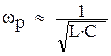 .
.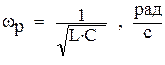
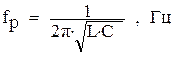
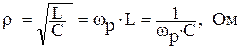
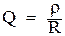 - добротность колебательного контура;
- добротность колебательного контура;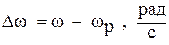 - абсолютная расстройка;
- абсолютная расстройка;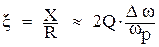 - обобщённая расстройка;
- обобщённая расстройка; - полоса пропускания контура по уровню 0.707;
- полоса пропускания контура по уровню 0.707;