Пояснения к изучаемым вопросам. Эти вопросы удобнее всего изучать по [1,3,8]

Эти вопросы удобнее всего изучать по [1,3,8]. Необходимо приобрести навык в решении задач.

 

Принятые условные обозначения:

Nв – число ветвей;                       I₁, I₂ или I1, I2 – токи в ветвях;

Nу – число узлов;                        P – мощность в цепи постоянного тока.

 

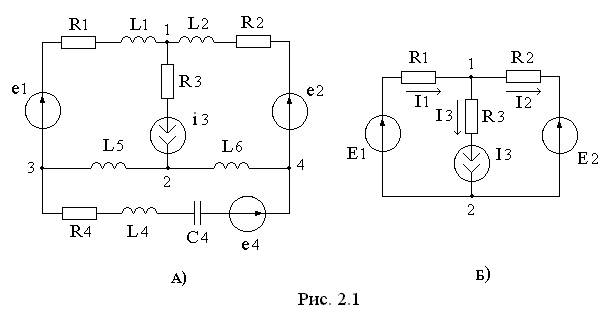
С помощью первого и второго законов Кирхгофа можно рассчитать любую цепь. Так, например, в цепи (рис. 2.1.А) шесть ветвей, одна из них содержит источник тока. Ток в этой ветви равен силе тока источника i3. Значения токов в остальных пяти ветвях неизвестны. Для определения их значений надо составить 5 уравнений.

В цепи четыре узла: Nу = 4. Число независимых уравнений, составленных по первому закону Кирхгофа, определяется:

Nу –1 = 3.

Оставшиеся два уравнения надо составить по второму закону Кирхгофа, выбрав любые два контура, не содержащих источник тока (так как падение напряжения на зажимах источника тока – неизвестная величина).

Если в данной цепи действуют источники постоянного напряжения и тока, то на эквивалентной схеме в ветвях с индуктивными и емкостным элементами появляются участки короткого замыкания и разомкнутый участок цепи (рисунок 2.1.Б). Тогда схема будет иметь два узла (Nу = 2) и три ветви (Nв = 3). Ток в ветви, содержащей источник тока, равен силе тока источника I3. Для определения двух других токов надо составить одно уравнение по первому закону Кирхгофа и ещё одно уравнение по второму закону Кирхгофа.

Для того чтобы записать уравнение по первому закону Кирхгофа необходимо произвольно задать направления токов в ветвях:

I1 - I2 - I3 = 0

Для контура, не содержащего источник тока (с элементами: Е1, R1, Е2, R2), следует произвольно задать направление обхода (например, по часовой стрелке) и записать уравнение по второму закону Кирхгофа:

 R1 I1 + R2 I2 = E1 – Е2

Решив систему двух уравнений с двумя неизвестными, можно найти токи.

Суммарная потребляемая мощность в резистивной цепи:

.

Мощность источника электрической энергии определяется как произведение значений падения напряжения на зажимах источника и тока в ветви с источником, причём значение мощности будет положительно, если положительные направления векторов тока и падения напряжения взаимно противоположны (обратите внимание на то, что направление вектора э.д.с. противоположно направлению вектора напряжения). Суммарная мощность источников цепи, представленной на рисунке 2.1.Б:

Уравнение баланса мощности:

 

2.3.  Режим гармонических колебаний в электрических цепях.

 

Основные изучаемые вопросы

1. Понятие о физических процессах в электрических цепях, описываемых с помощью гармонических периодических функций. Параметры гармонической функции: амплитуда, фаза, начальная фаза, циклическая частота, период, угловая частота. Действующее (среднеквадратичное) и среднее значения гармонической функции.

2. Символический метод анализа гармонических колебаний в электрических цепях (метод комплексных амплитуд). Понятия о мгновенном комплексном значении, комплексном амплитудном значении, комплексном действующем значении, операторе вращения, векторной диаграмме. Спектральное представление гармонического напряжения (тока).

3. Законы Ома и Кирхгофа в комплексной форме. Прохождение гармонического тока через резистивный, индуктивный, ёмкостный элементы. Понятие комплексного сопротивления и комплексной проводимости. Изображение комплексных значений тока и напряжения в виде векторов в комплексной плоскости.

4. Энергетические соотношения в простейших цепях при гармоническом воздействии. Мгновенная, средняя (активная), реактивная, полная, комплексная мощности. Баланс мощностей в цепи.

5. Расчёт цепей с использованием метода комплексных амплитуд и ранее изученных методов (метода контурных токов, метода узловых напряжений и других). 

 

Принятые условные обозначения:

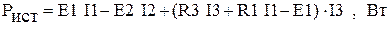
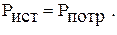
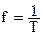 , (Гц) – циклическая частота гармонического колебания;

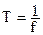 , (с) – период гармонического колебания;

 , (рад/с) - угловая частота;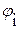

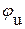, , (радианов или градусов) - начальные фазовые углы тока и напряжения;

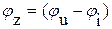 - начальный фазовый угол сопротивления (сдвиг фаз между напряжением и током);

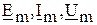- комплексные амплитуды э.д.с., тока, напряжения;

- амплитуды э.д.с., тока, напряжения;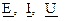

 - комплексные действующие значения э.д.с., тока, напряжения;

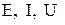- действующие значения э.д.с., тока, напряжения;

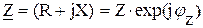 - комплексное сопротивление;

Z – модуль комплексного сопротивления;

R – вещественная часть комплексного сопротивления (резистивное сопротивление);

X – мнимая часть комплексного сопротивления (реактивное сопротивление);

 ,  - комплексная мощность;

P, (Вт) – активная (средняя) мощность;

Q, (вар) – реактивная мощность;

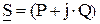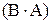p(t), (BA) – мгновенная мощность.