
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление определенного интеграла
Интеграл с переменным верхним пределом Пусть на отрезке
Рис. 2 Очевидно, что если изменяется верхний предел, то изменяется и значение интеграла, так как определенный интеграл – это число, связанное с пределами интегрирования. Обозначим Определение: Функция Теорема: Если функция Аналогичную теорему можно доказать для случая переменного нижнего предела. Замечание. Таким образом, можно утверждать, что всякая непрерывная на отрезке
Теорема Ньютона-Лейбница Теорема: Если функция
Это выражение известно под названием формулы Ньютона – Лейбница. Доказательство: Пусть
Это равенство справедливо для любого
Следовательно,
Полагая в этом равенстве
Заменив переменную t на переменную
Теорема доказана. Иногда применяют обозначение двойной подстановки При вычислении определенных интегралов используются те же приемы и методы, которые были изучены при нахождении неопределенных интегралов. Примеры. Вычислить следующие интегралы: 1. 2. 3. 4.
Замена переменной в определенном интеграле Теорема: Пусть дан интеграл 1) j (a) = а, j (b) = b (т.е. при изменении 2) j (t) и j ¢(t) непрерывны на отрезке [ a, b ], 3) сложная функция f (j (t)) определена и непрерывна на отрезке [ a, b ], то
Тогда Замечание 1. При вычислении определенного интеграла по формуле (6) не надо возвращаться к старой переменной, т.к. уже получено числовое значение интеграла. Пример.
= Замечание 2. При замене переменной в определенном интеграле следует следить за непрерывностью вводимой функции на рассматриваемом отрезке интегрирования. В противном случае формальное применение формулы приводит к абсурду. Например,
Применим к этому интегралу тригонометрическую подстановку, получим Таким образом, два способа нахождения интеграла дают различные результаты. Это произошло из-за того, что введенная функция Интегрирование по частям в определенном интеграле Если функции
Пример.
=
Интегрирование четных и нечетных функций на отрезке, симметричном относительно нуля Теорема. Определенный интеграл с противоположными пределами интегрирования от непрерывной нечетной функции равен нулю, т.е.
Доказательство. Пусть
В первом из интегралов сделаем замену переменных, положив
Теорема. Определенный интеграл с противоположными пределами интегрирования от непрерывной четной функции равен удвоенному интегралу от этой функции, взятому по правой (левой) половине отрезка интегрирования, т.е.
Доказательство теоремы аналогично предыдущему.
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
Рассматривается расширение понятия определенного интеграла по двум направлениям: 1) пределы интегрирования уходят в бесконечность; 2) интегрирование на конечном отрезке функций, имеющих разрыв 2-го рода.
|
|||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 98; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.85.33 (0.008 с.) |
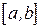 задана непрерывная функция
задана непрерывная функция 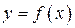 . Выберем на отрезке любое значение
. Выберем на отрезке любое значение  и рассмотрим интеграл в пределах от
и рассмотрим интеграл в пределах от 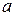 до
до  :
:  (см. рис. 2).
(см. рис. 2).
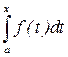 =
=  .
.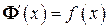 или
или  .
.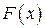 – какая- либо первообразная от непрерывной функции
– какая- либо первообразная от непрерывной функции 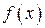 , то
, то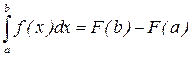 (5)
(5) .
. из рассматриваемого интервала. Положим
из рассматриваемого интервала. Положим 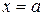 :
: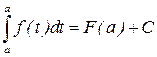 .
. , то есть
, то есть  . Тогда можно записать
. Тогда можно записать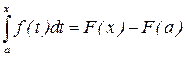 .
.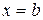 , получим:
, получим:
 .
.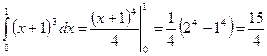


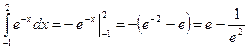
 , где функция
, где функция  . Если при этом:
. Если при этом: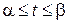 значения функции
значения функции  не выходят за интервал
не выходят за интервал 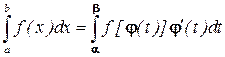 (6)
(6)
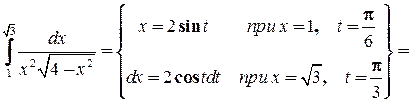
 =
=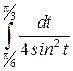 =
= 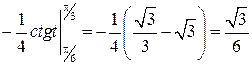 .
. ,
, .
.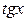 имеет на отрезке интегрирования разрыв (в точке
имеет на отрезке интегрирования разрыв (в точке  и
и 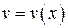 непрерывны на отрезке
непрерывны на отрезке  (7)
(7) =
=  =
=  =
=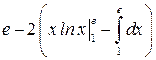 =
= 
 .
. . Вычислим интеграл
. Вычислим интеграл
 . Тогда, учитывая нечетность функции
. Тогда, учитывая нечетность функции 
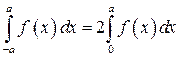 .
.


