Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача о площади криволинейной трапецииСтр 1 из 3Следующая ⇒
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Задача о площади криволинейной трапеции Пусть на отрезке Рис.1 Определение 1: Криволинейной трапецией называется фигура, ограниченная кривой Ставится задача: найти площадь криволинейной трапеции Рассмотрим произвольный отрезок
Полученную площадь ступенчатой фигуры можно принять за приближенное значение искомой площади криволинейной трапеции
Увеличивая число точек разбиения отрезка и одновременно уменьшая длины всех элементарных отрезков, в пределе получим площадь криволинейной трапеции
где
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
Рассматривается расширение понятия определенного интеграла по двум направлениям: 1) пределы интегрирования уходят в бесконечность; 2) интегрирование на конечном отрезке функций, имеющих разрыв 2-го рода.
ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Вычисление объемов тел Вычисление объема тела по известным площадям его параллельных сечений
Рис. 11.
Пусть имеется тело объема V. Площадь любого поперечного сечения тела S известна как непрерывная функция S = S (x). Разобьем тело на “слои” поперечными сечениями, проходящими через точки х i разбиения отрезка [ a, b ] (см. рис. 11). Так как на каком- либо промежуточном отрезке разбиения [ xi -1, xi ] функция S (x) непрерывна, то принимает на нем наибольшее и наименьшее значения. Обозначим их соответственно Mi и mi.
Если на этих наибольшем и наименьшем сечениях построить цилиндры с образующими, параллельными оси х, то объемы этих цилиндров будут соответственно равны Mi D xi и mi D xi, при этом D xi = xi - xi -1. Произведя такие построения для всех отрезков разбиения, получим цилиндры, объемы которых равны соответственно При стремлении к нулю шага разбиения l, эти суммы имеют общий предел:
Таким образом, объем тела может быть найден по формуле:
Недостатком этой формулы является то, что для нахождения объема необходимо знать функцию S (x), что весьма проблематично для сложных тел. Пример. Найти объем шара радиуса R.
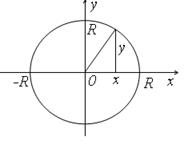
Рис. 12. В поперечных сечениях шара получаются окружности переменного радиуса Тогда функция площадей сечений имеет вид: S (x) = Получаем объем шара:
Объем тел вращения Рассмотрим кривую, заданную уравнением
Рис. 13. Так как каждое сечение тела плоскостью
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Задача о площади криволинейной трапеции Пусть на отрезке Рис.1 Определение 1: Криволинейной трапецией называется фигура, ограниченная кривой Ставится задача: найти площадь криволинейной трапеции
Рассмотрим произвольный отрезок
Полученную площадь ступенчатой фигуры можно принять за приближенное значение искомой площади криволинейной трапеции
Увеличивая число точек разбиения отрезка и одновременно уменьшая длины всех элементарных отрезков, в пределе получим площадь криволинейной трапеции
где
|
||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 88; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.96.146 (0.015 с.) |
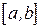 задана непрерывная функция
задана непрерывная функция  , причем
, причем  на этом отрезке. Построим график функции на
на этом отрезке. Построим график функции на 
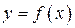 , прямыми
, прямыми 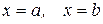 и частью оси
и частью оси 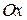 (
( . Для приближенного решения поставленной задачи разобьём отрезок
. Для приближенного решения поставленной задачи разобьём отрезок  частей точками
частей точками  ; где
; где 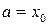 ,
,  . В результате криволинейная трапеция разобьётся на узкие полоски, которые в общем случае также являются криволинейными трапециями. Но чем меньше ширина полоски, тем меньше эта трапеция отличается от прямоугольника.
. В результате криволинейная трапеция разобьётся на узкие полоски, которые в общем случае также являются криволинейными трапециями. Но чем меньше ширина полоски, тем меньше эта трапеция отличается от прямоугольника. длины
длины 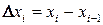 , где
, где 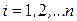 . На каждом отрезке выберем произвольную точку
. На каждом отрезке выберем произвольную точку  , то есть
, то есть 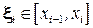 , и подсчитаем значение функции в этой точке
, и подсчитаем значение функции в этой точке 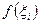 . Заменим
. Заменим 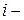 ю криволинейную трапецию на прямоугольник с тем же основанием и высотой, равной
ю криволинейную трапецию на прямоугольник с тем же основанием и высотой, равной 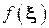 . Сделав такую замену на всех
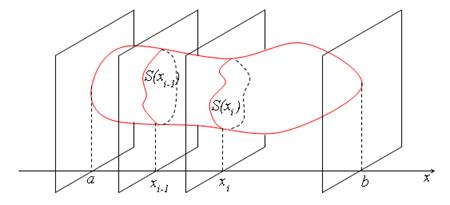
. Сделав такую замену на всех 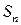 может быть подсчитана по формуле:
может быть подсчитана по формуле: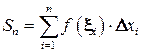
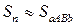
 ,
,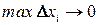 при
при 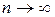 .
.
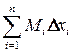 и
и  .
.
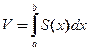
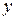 . В зависимости от текущей координаты
. В зависимости от текущей координаты 
 этот радиус выражается по формуле
этот радиус выражается по формуле 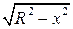 (см. рис.12).
(см. рис.12). .
.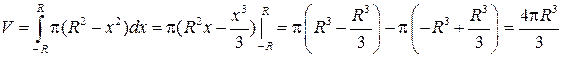 .
.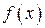 непрерывна на отрезке
непрерывна на отрезке 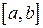 . Если соответствующую ей криволинейную трапецию с основанием
. Если соответствующую ей криволинейную трапецию с основанием 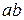 вращать вокруг оси Ох, то получим так называемое тело вращения.
вращать вокруг оси Ох, то получим так называемое тело вращения.
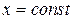 представляет собой круг радиуса
представляет собой круг радиуса 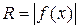 , то объем тела вращения может быть найден по полученной выше формуле:
, то объем тела вращения может быть найден по полученной выше формуле: