Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
РГР № 1. Часть 2. Электростатика. Электрический токСодержание книги
Поиск на нашем сайте
Таблица вариантов (номер варианта определяется по последней цифре в шифре зачётной книжки) Таблица 5
Перед решением задач данной контрольной работы необходимо хорошо изучить соответствующие темы курса общей физики, указанные в следующей таблице.
Таблица 6
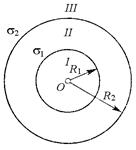
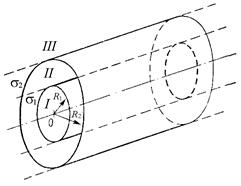
301. Два одинаковых заряженных проводящих шарика, находящиеся в воздухе, плотность материала которых r = 1600 кг/м3, подвешены в одной точке на тонких невесомых нерастяжимых нитях одинаковой длины; при этом нити разошлись на некоторый определенный угол. Затем шарики погрузили в керосин. Определите диэлектрическую проницаемость e керосина, если угол расхождения нитей при погружении шариков в керосин остался неизменным. 302. По тонкому кольцу радиусом R = 20 см равномерно распределен электрический заряд с линейной плотностью t = 0,2 мкКл/м. Определите напряженность Е электрического поля, создаваемого распределенным зарядом в точке, находящейся на оси кольца на расстоянии h = 2 R от его центра. 303. В вершинах правильного треугольника со стороной длиной а = 10 см находятся точечные электрические заряды q 1 = 10 мкКл, q 2 = 20 мкКл и q 3 = 30 мкКл. Определите силу F, действующую на заряд q 1 со стороны двух других зарядов. 304. Электрическое поле создано двумя точечными электрическими зарядами q 1 = 10 нКл и q 2 = – 20 нКл, находящимися в вакууме на расстоянии d = 20 см друг от друга. Определите напряженность Е электрического поля в точке, удаленной от первого заряда на расстояние r 1 = 30 см и от второго заряда на расстояние r 2 = 50 см. 305. Тонкий прямой бесконечно длинный стержень равномерно заряжен с линейной плотностью t = 10 мкКл/м. Определите силу F, действующую на точечный заряд q = 10 нКл, находящийся вблизи средней части стержня на расстоянии a = 20 см, малом по сравнению с его длиной. 306. По тонкому полукольцу равномерно распределен электрический заряд q = 20 мкКл с линейной плотностью t = 0,1 мкКл/м. Определите напряженность Е электрического поля, создаваемого распределенным зарядом в точке, совпадающей с центром кольца. 307. В вершинах квадрата находятся одинаковые электрические заряды q = 0,3 нКл каждый. Какой отрицательный электрический заряд q o нужно поместить в центре квадрата, чтобы сила взаимного отталкивания положительных зарядов была уравновешена силой притяжения отрицательного заряда? 308. Бесконечно протяженная вертикальная плоскость несет электрический заряд, равномерно распределенный с поверхностной плотностью s = 400 мкКл/м2. К плоскости на тонкой невесомой нерастяжимой нити подвешен одноименно заряженный шарик массой m = 10 г. Определите электрический заряд q шарика, если нить с плоскостью образует угол a = 30°. 309. Свободные точечные электрические заряды q 1 = 180 нКл и q 2 = 720 нКл закреплены на расстоянии l = 60 см друг от друга. На каком расстоянии r от первого заряда на прямой, проходящей через оба заряда, находится точка, в которой нужно поместить третий точечный электрический заряд q 3 так, чтобы система зарядов находилась в равновесии. Определите величину и знак этого заряда. Устойчивое или неустойчивое будет равновесие? 310. На отрезке тонкого прямого проводника длиной l = 10 см равномерно распределен электрический заряд с линейной плотностью t = 3 мкКл/м. Вычислите напряженность Е электрического поля, создаваемую этим зарядом в точке, расположенной на оси проводника и удаленной от ближайшего конца проводника на расстояние, равное длине этого отрезка. 311. На двух концентрических сферах радиусами R 1 = R и R 2 = 2 R равномерно распределены электрические заряды с поверхностными плотностями s1 = 4s и s2 = s, где s = 30 нКл/м2 (рис. 1). Используя теорему Остроградского – Гаусса, найдите зависимость Е (r) напряженности электрического поля от координаты для трех областей: I, II и III. Вычислите напряженность Е электрического поля в точке, удаленной от центра сфер на расстояние r = 1,5 R, и укажите направление вектора Е. Постройте график зависимости Е (r).
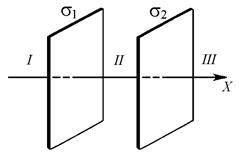
312. Две длинные тонкостенные коаксиальные трубки радиусами R 1 = 2 см и R 2 = 4 см несут электрические заряды, равномерно распределенные с линейными плотностями t1 = 1 нКл/м и t2 = –0,5 нКл/м. Пространство между трубками заполнено эбонитом. Определите напряженность E электрического поля в точках, находящихся от оси трубок на расстояниях r 1 = 1 см, r 2 = 3 см, r 3 = 5 см. Постройте график зависимости Е (r). 313. На двух бесконечных параллельных плоскостях равномерно распределены электрические заряды с поверхностными плотностями s1 = 2s и s2 = s, где s = 80 нКл/м2 (рис. 2). Используя теорему Остроградского – Гаусса и принцип суперпозиции электрических полей, найдите выражение зависимости Е (x) напряженности электрического поля от координаты для трех областей: I, II и III. Вычислите напряженность Е электрического поля в точке, расположенной слева от плоскостей (в области I), и укажите направление вектора Е. Постройте график зависимости Е (x) напряженности электрического поля от координаты x вдоль линии, перпендикулярной пластинам.
314. На металлической сфере радиусом R = 10 см находится электрический заряд q = 1 нКл. Определите напряженность Е электрического поля в точках, отстоящих от центра сферы на расстояниях: 1) r 1 = 8 см (внутри сферы); 2) r 2 = 10 см (на поверхности сферы); 3) r 3 = 15 см (вне сферы). Постройте график зависимости Е (r). 315. На двух коаксиальных бесконечно длинных цилиндрах радиусами R 1 = R и R 2 = 2 R равномерно распределены электрические заряды с поверхностными плотностями s1 = 2s и s2 = – s, где s = 60 нКл/м2 (рис. 3). Используя теорему Остроградского – Гаусса, найдите зависимость Е (r) напряженности электрического поля от координаты для трех областей: I, II и III. Вычислите напряженность Е электрического поля в точке, удаленной от оси цилиндров на расстояние r = 1,5 R, и укажите направление вектора Е. Постройте график зависимости Е (r).
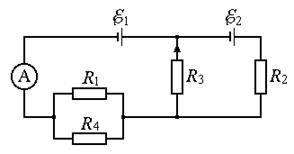
316. На двух концентрических сферах радиусами R 1 = R и R 2 = 2 R равномерно распределены электрические заряды с поверхностными плотностями s1 = – 4s и s2 = s, где s = 30 нКл/м2 (рис. 1). Используя теорему Остроградского – Гаусса, найдите зависимость Е (r) напряженности электрического поля от координаты для трех областей: I, II и III. Вычислите напряженность Е электрического поля в точке, удаленной от центра сфер на расстояние r = 1,5 R, и укажите направление вектора Е. Постройте график зависимости Е (r). 317. Длинный парафиновый цилиндр радиусом R = 2 см несет электрический заряд, равномерно распределенный с объемной плотностью r = 10 нКл/м3. Определите напряженность Е электрического поля в точках, равноудаленных от концов цилиндра и находящихся от оси цилиндра на расстоянии: 1) r 1 = 1 см; 2) r 2 = 2 см; 3) r 3 = 3 см. Постройте график зависимости Е (r). 318. На двух бесконечных параллельных плоскостях равномерно распределены электрические заряды с поверхностными плотностями s1 = –2s и s2 = s, где s = 80 нКл/м2 (рис. 2). Используя теорему Остроградского – Гаусса и принцип суперпозиции электрических полей, найдите выражение зависимости Е (x) напряженности электрического поля от координаты для трех областей: I, II и III. Вычислите напряженность Е электрического поля в точке, расположенной между плоскостями (в области II), и укажите направление вектора Е. Постройте график зависимости Е (x) напряженности электрического поля от координаты x вдоль линии, перпендикулярной пластинам. 319. Сплошной эбонитовый шар радиусом R = 5 см несет электрический заряд, равномерно распределенный с объемной плотностью r = 10 нКл/м3. Определите напряженность Е электрического поля в точках, отстоящих от центра шара на расстояниях: 1) r 1 = 3 см (внутри шара); 2) r 2 = 5 см (на поверхности шара); 3) r 2 = 10 см (вне шара). Постройте график зависимости Е (r). 320. На двух коаксиальных бесконечно длинных цилиндрах радиусами R 1 = R и R 2 = 2 R равномерно распределены электрические заряды с поверхностными плотностями s1 = – 2s и s2 = s, где s = 60 нКл/м2 (рис. 3). Используя теорему Остроградского – Гаусса, найдите зависимость Е (r) напряженности электрического поля от координаты для трех областей: I, II и III. Вычислите напряженность Е электрического поля в точке, удаленной от оси цилиндров на расстояние r = 1,5 R, и укажите направление вектора Е. Постройте график зависимости Е (r). 321. Сто (N = 100) маленьких одинаковых капель ртути, находящиеся в воздухе и заряженные до потенциала jo = 20 В, слились в одну большую каплю. Каков потенциал j образовавшейся капли? 322. Ионы меди Cu++ и калия K+ без начальной скорости в однородном электрическом поле прошли одинаковую ускоряющую разность потенциалов. Найдите отношение v1/v2 скоростей движения этих ионов. 323. На отрезке тонкого прямого проводника равномерно распределен электрический заряд с линейной плотностью t = 10 нКл/м. Вычислите потенциал j электрического поля, создаваемый этим зарядом в точке, расположенной на оси проводника и удаленной от ближайшего конца проводника на расстояние, равное длине этого отрезка. 324. Тонкий стержень, равномерно заряженный с линейной плотностью t == 300 нКл/м, согнут в кольцо радиусом R = 10 см. Какую работу А надо совершить силам электростатического поля, чтобы перенести точечный электрический заряд q = 5 нКл из центра кольца в точку, расположенную на оси кольца на расстоянии h = 20 см от его центра? 325. Четыре одинаковых точечных электрических заряда q = 10 нКл каждый расположены в вершинах квадрата со стороной длиной a = 10 см. Определите потенциальную энергию П системы этих зарядов. 326. Точечный электрический заряд q = 1 нКл переместился в направлении перпендикулярном тонкой бесконечно длинной равномерно заряженной нити с расстояния r 1 = 2 см до расстояния r 2 = 5 см; при этом силами электрического поля по перемещению заряда была совершена работа A = 50 мкДж. Определите линейную плотность t электрического заряда, распределенного на нити. 327. Электростатическое поле создается шаром радиусом R = 8 см, равномерно заряженным с объемной плотностью r = 10 нКл/м3. Определите разность потенциалов (j1 - j2) между двумя точками этого поля, лежащими от центра шара на расстояниях r 1 = 10 см и r 2 = 15 см. 328. Тонкий стержень, равномерно заряженный с линейной плотностью t == 133 нКл/м, согнут в полукольцо. Какую работу А нужно совершить силам электростатического поля, чтобы перенести точечный электрический заряд q = 6,7 нКл из центра полукольца в бесконечность? 329. Четыре тонких прямых стержня, равномерно заряженные с линейной плотностью t = 1,33 нКл/м, образуют квадрат. Определите потенциал j электрического поля в центре квадрата. 330. Протон, начальная скорость движения которого vo = 100 км/с, влетает в однородное электрическое поле напряженностью Е = 300 В/см так, что вектор скорости совпадает с направлением линий напряженности поля. Какой путь l должен пройти протон в направлении линий поля, чтобы его скорость движения увеличилась в n = 2 раза? 331. В плоский воздушный конденсатор вдвинули плитку парафина толщиной h = 1 см, которая вплотную прилегает к его пластинам. На какую величину D d нужно увеличить расстояние между пластинами конденсатора, чтобы получить прежнюю электроемкость? 332. Уединенная металлическая сфера электроемкостью С = 10 пФ заряжена до потенциала j = 3 кВ. Определите энергию W электрического поля, заключенную в сферическом слое, ограниченном сферой и концентрической с ней сферической поверхностью, радиус которой в n = 3 раза больше радиуса сферы. 333. Конденсатор электроемкостью С 1 = 0,2 мкФ был заряжен до разности потенциалов U 1 = 320 В. После того как его соединили параллельно со вторым конденсатором, заряженным до разности потенциалов U 2 = 450 В, напряжение на нем увеличилось до величины U = 400 В. Вычислите электроемкость С 2 второго конденсатора. 334. Плоский конденсатор, между пластинами которого находится фарфор, имеет электроемкость С 1 = 111 пФ. Конденсатор зарядили до разности потенциалов U 1 = 600 В и отключили от источника питания. Пренебрегая трением диэлектрика о пластины конденсатора, определите работу А, которую нужно совершить, чтобы вынуть диэлектрик из конденсатора. 335. Шар радиусом R 1 = 6 см заряжен до потенциала j1 = 300 В, а шар радиусом R 2 = 4 см – до потенциала j2 = 500 В. Шары соединили металлическим проводником. Пренебрегая электроемкостью соединительного проводника, определите потенциал j шаров после их соединения. 336. Конденсатор электроемкостью C 1 = 600 пФ зарядили до разности потенциалов U = 1,5 кВ и отключили от источника питания. Затем к конденсатору присоединили параллельно второй, незаряженный конденсатор электроемкостью С 2 = 400 пФ. Определите энергию D W, израсходованную на образование искры, проскочившей при соединении конденсаторов. 337. Плоский конденсатор, между пластинами которого находится плотно прилегающая стеклянная пластинка, заряжен до разности потенциалов U 1 = 100 В. Какова будет разность потенциалов U 2, если вынуть стеклянную пластинку из конденсатора? 338. Плоский воздушный конденсатор состоит из двух круглых пластин радиусом r = 10 см каждая. Расстояние между пластинами d 1 = 1 см. Конденсатор зарядили до разности потенциалов U = 1,2 кВ и отключили от источника питания. Какую работу А нужно совершить, чтобы, удаляя пластины друг от друга, увеличить расстояние между ними до d 2 = 3,5 см? 339. Конденсатор электроемкостью C 1 = 0,6 мкФ был заряжен до разности потенциалов U 1 = 300 В и соединен со вторым конденсатором электроемкостью С 2 = 0,4 мкФ, заряженным до разности потенциалов U 2 = 150 В. Найдите электрический заряд D q, перетекший с пластин первого конденсатора на второй. 340. Сплошной парафиновый шар радиусом R = 10 см равномерно заряжен с объемной плотностью r = 10 нКл/м3. Определите энергию W электрического поля, сосредоточенную в самом шаре. 341. При силе тока I 1 = 1 А во внешней цепи батареи аккумуляторов выделяется мощность Р 1 = 10 Вт, а при силе тока I 2 = 3 А – соответственно мощность Р 2 = 18 Вт. Определите внутреннее сопротивление r и ЭДС Е батареи. 342. Сила тока в проводнике сопротивлением R = 3 Ом равномерно увеличивается. За время t = 8 с в проводнике выделилось количество теплоты Q = 200 Дж. Определите электрический заряд q, прошедший за это время по проводнику, если известно, что в момент времени, принятый за начальный (t o = 0), сила тока в проводнике I o = 0 А. 343. К источнику тока с ЭДС E = 1,5 В присоединили катушку с сопротивлением R = 0,1 Ом; при этом амперметр показал силу тока I 1 = 0,5 А. Когда же к источнику тока присоединили последовательно еще один источник тока с такой же ЭДС, то сила тока в той же катушке оказалась I 2 = 0,4 А. Определите внутренние сопротивления r 1 и r 2 соответственно первого и второго источников тока. 344. Сила тока в проводнике сопротивлением R = 12 Ом равномерно уменьшается от I o = 5 А до I = 0 А в течение времени t = 10 с. Определите количество теплоты Q, выделившейся в этом проводнике за указанный промежуток времени. 345. К зажимам батареи аккумуляторов присоединен нагреватель. ЭДС батареи E = 24 В, ее внутреннее сопротивление r = 1 Ом. Нагреватель, включенный в электрическую цепь, потребляет мощность P = 80 Вт. Вычислите силу тока I в цепи и КПД h нагревателя. 346. Сила тока в проводнике сопротивлением R = 3 Ом равномерно увеличивается от I o = 0 А до некоторого максимального значения в течение времени t = 10 с. За это время в проводнике выделилось количество теплоты Q = 1 кДж. Определите скорость нарастания D I /D t силы тока в проводнике. 347. В электрическую сеть с напряжением U = 100 В подключили катушку с сопротивлением R 1 = 2 кОм и вольтметр, соединенные последовательно; при этом вольтметр показал напряжение U 1 = 80 В. Когда катушку заменили другой, вольтметр показал напряжение U 2 = 60 В. Определите сопротивление R 2 другой катушки. 348. Сила тока в проводнике изменяется со временем согласно уравнению I = I o sin w t, где амплитуда силы тока I o = 10 А, циклическая частота w = 50 p с-1. Найдите электрический заряд q, прошедший через поперечное сечение проводника за время t = T /2, где T - период колебания силы тока в проводнике. 349. При внешнем сопротивлении R 1 = 50 Ом сила тока в электрической цепи I 1 = 0,2 А, а при внешнем сопротивлении R 2 = 110 Oм сила тока в цепи I 2 = 0,1 А. Определите силу тока I кз короткого замыкания источника ЭДС. 350. При выключении источника тока сила тока в электрической цепи уменьшается со временем согласно уравнению I = I o 351. Две батареи аккумуляторов с ЭДС E1 = E2 = 100 В и четыре резистора с сопротивлениями R 1 = 20 Ом, R 2 = 10 Ом, R 3 = 40 Ом и R 4 = 30 Ом соединены, как показано на рис. 4. Пренебрегая внутренними сопротивлениями батарей аккумуляторов, найдите силу тока I A, которую показывает амперметр.
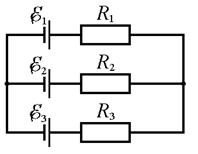
352. Три источника тока с ЭДС E1 = 11 В, E2 = 4 В и E3 = 6 В и три реостата с сопротивлениями R 1 = 5 Ом, R 2 = 10 Ом и R 3 = 2 Ом соединены, как показано на рисунке 5. Пренебрегая внутренними сопротивлениями источников тока, определите силу токов Ii, текущих в каждом реостате. 353. Две батареи аккумуляторов с одинаковыми ЭДС, два резистора с одинаковыми сопротивлениями R 1 = R 2 = 100 Ом и вольтметр с сопротивлением R V = 150 Ом соединены, как показано на рисунке 6. Пренебрегая внутренними сопротивлениями батареи аккумуляторов, найдите их ЭДС E1 и E2, если вольтметр показывает напряжение U = 150 В.
354. Две батареи аккумуляторов с ЭДС E1 = 130 В и E2 = 117 В и три резистора с сопротивлениями R 1 = 1 Ом, R 2 = 0,6 Ом и R 3 = 24 Ом соединены, как показано на рисунке 7. Пренебрегая внутренними сопротивлениями батарей аккумуляторов, определите токи Ii, текущие в отдельных ветвях электрической цепи. 355. Три резистора с сопротивлениями R 1 = 5 Ом, R 2 = 1 Ом, R 3 = 3 Ом и источник тока с ЭДС E1 = 1,4 В соединены как показано на рисунке 8. Пренебрегая внутренними сопротивлениями источников тока, определите ЭДС E2 источника тока, который надо подключить в электрическую цепь между точками A и B, чтобы через резистор с сопротивлением R 3 протекал ток I 3 = 1 А в направлении, указанном стрелкой.
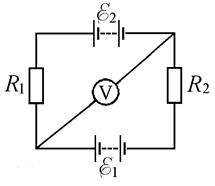
356. Два гальванических элемента имеют ЭДС E1 = 2 В и E2 = 4 В, резистор R 1 имеет сопротивление 0,5 Ом (см. рис. 9). На резисторе с сопротивлением R 2 падение напряжения U 2 = 1 В, причем ток через этот резистор направлен справа налево. Пренебрегая внутренними сопротивлениями гальванических элементов, найдите силу тока I A, которую показывает амперметр. 357. Три батареи аккумуляторов с ЭДС E1 = 1 В, E2 = 3 В и E3 = 5 В и три резистора с сопротивлениями R 1 = 2 Ом, R 2 = 4 Ом и R 3 = 2 Ом соединены, как показано на рисунке 10. Пренебрегая внутренними сопротивлениями батарей аккумуляторов, определите силу тока Ii, текущего в каждой ветви электрической цепи.
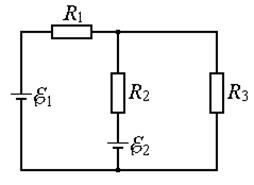
358. Источник тока имеет ЭДС E = 2 В, резисторы имеют сопротивления R 1 = 30 Ом, R 2 = 45 Ом и R 3 = 200 Ом (рис. 11). Пренебрегая внутренним сопротивлением источника тока, найдите силу токов Ii, текущих в каждой ветви мостика Уитстона, если гальванометр показывает силу тока I г= 0 А. 359. Два гальванических элемента имеют ЭДС E1 = 2 В и E2 = 3 В, резистор R 2 имеет сопротивление 1,5 кОм, сопротивление амперметра R A = 0,5 кОм (см. рис. 12). На резисторе с сопротивлением R 1 падение напряжения U 1 = 1 В, причем ток через этот резистор течет сверху вниз. Пренебрегая внутренними сопротивлениями гальванических элементов, найдите силу тока I A, которую показывает амперметр. 360. Два источника тока с ЭДС E1 = 4 В и E2 = 3 В и три резистора с сопротивлениями R 1 = 2 Ом, R 2 = 6 Ом и R 3 = 1 Ом соединены, как показано на рисунке 13. Пренебрегая внутренними сопротивлениями источников тока, определить силу тока I 3 в резисторе с сопротивлением R 3 и падение напряжения U 3 на концах этого резистора.
361. По тонкому прямому проводу длиной l = 500 м течет ток I = 20 А. Определите суммарный импульс p электронов в проводе. 362. В металле концентрация свободных электронов n = 1029 м-3. Определите среднее число á z ñ соударений, которые испытывает свободный электрон с ионами кристаллической решетки металла за время t = 1 с, если удельная проводимость металла g = 10 МСм/м. 363. Термопара состоит из резистора с сопротивлением R = 4 Ом и гальванометра с сопротивлением R г = 80 Ом. При разности температур спаев D t = 50°С сила тока в электрической цепи I = 26 мкА. Определите постоянную a термопары. 364. В медном проводнике длиной l = 2 м и площадью поперечного сечения S = 0,4 мм2 течет электрический ток; при этом за время t = 1 с выделяется количество теплоты Q = 0,35 Дж. Определите число N электронов, которое проходит за это время через поперечное сечение проводника. 365. Металлический стержень длиной l = 10 м движется поступательно вдоль своей оси со скоростью v = 200 м/с. Определите электрический заряд q, который протечет через гальванометр, подключенный с помощью неподвижного проводника к концам стержня при его резком торможении, если сопротивление всей электрической цепи, включая цепь гальванометра, R = 10 мОм. 366. Термопара медь – константан с постоянной a = 43 мкВ/К и резистор с сопротивлением R = 5 Ом присоединена к гальванометру, сопротивление которого R г = 100 Ом. Один спай термопары погружен в тающий лед, а другой – в горячую жидкость. Определите температуру t этой жидкости, если сила тока в электрической цепи I = 37 мкА. 367. При прохождении по алюминиевому проводнику объемом V = 10 см3 постоянного электрического тока за время t = 5 мин в нем выделилось количество теплоты Q = 2,3 кДж. Определите напряженность Е электрического поля в проводнике. 368. Металлический диск радиусом R = 0,5 м вращается равномерно с угловой скоростью w = 104 рад/с относительно неподвижной оси, перпендикулярной плоскости диска и проходящей через его центр. Диск включен в электрическую цепь при помощи скользящих контактов, касающихся оси диска и его окружности. Определите разность потенциалов U между центром диска и его крайними точками. 369. Термопара висмут – железо с постоянной a = 92 мкВ/К и сопротивлением R = 5 Ом присоединена к гальванометру, сопротивление которого R г = 110 Ом. Какую силу тока I в электрической цепи показывает гальванометр, если температура холодного спая термопары t 1 = 0 °С, а температура горячего спая t 2 = 100 °С? 370. В медном проводнике плотность электрического тока j = 10 А/см2. Определите удельную тепловую мощность w электрического тока. 371. При электролизе раствора медного купороса (CuSO4) в течение времени t = 1 ч при силе тока I 2 = 1 А на катоде выделилась медь массой m 1 = 1,66 г. Определите коэффициент полезного действия h установки. 372. Посередине между электродами ионизационной камеры, расстояние между которыми d = 4 см и разность потенциалов U = 5 кВ, двигаясь параллельно электродам, пролетела a-частица и образовала на своем пути цепочку ионов. Через какое время t после пролета a-частицы ионы достигнут электродов, если подвижность ионов обоих знаков b = 2 см2/(В×с)? 373. Температура вольфрамового катода электронной лампы увеличилась от Т 1 = 2000 К до Т 2 = 2500 К. Определите, как и во сколько раз изменится при этом плотность тока насыщения. 374. При электролизе сульфата никеля (NiSO4) плотность тока, протекающего через электролит, j = 10 А/м2. Какое число N атомов никеля выделится на поверхности катода площадью S = 1 см2 за время t = 5 мин? 375. Расстояние между пластинами плоского конденсатора d = 1 см, площадь каждой пластины S = 100 см2. Определите силу тока насыщения I нас между его пластинами, если известно, что под действием внешнего ионизатора в объеме V o = 1 см3 пространства между пластинами конденсатора за время t = 1 с образуется число N = 108 пар ионов, каждый из которых несет один элементарный заряд. 376. В электронной лампе при температуре вольфрамового волоска катода T = 2000 К сила тока насыщения I нас = 2,86 мкА. Для вольфрама эмиссионная постоянная C = 6,02·105 А/(м2×К2). Определите диаметр d волоска катода, если его длина l = 2 см. 377. При электролизе водного раствора медного купороса (CuSO4) плотность электрического тока, протекающего через электролит, j = 80 А/м2. Определите скорость u (в мкм/ч) равномерного нарастания слоя меди на плоской поверхности металлической пластинки при электролизе. 378. Воздух между пластинами плоского воздушного конденсатора электроемкостью С = 6,6 пФ ионизируется внешним ионизатором, и при напряжении U = 450 В сила тока, текущего между пластинами конденсатора, I = 7 мкА. Заряд каждого иона равен элементарному заряду. Определите концентрацию n ионов между пластинами конденсатора, если насыщение не имеет места. 379. В электронной лампе при увеличении термодинамической температуры металлической нити накала от T 1 = 2380 К до Т 2 = 2381 К плотность тока насыщения увеличивается на n = 1 %. Определите работу выхода А электрона из металла. 380. При электролизе водного раствора нитрата серебра (AgNO3) была израсходована электрическая энергия W = 2,1 кДж; при этом на катоде выделилось серебро массой m = 500 мг. Определите разность потенциалов U между электродами, если коэффициент полезного действия установки h = 85 %. Вопросы для самоконтроля. РГР № 1. Часть 2. 1. Закон Кулона. Закон сохранения электрического заряда. Дискретность заряда. 2. Напряженность электрического поля. 3. Поток вектора напряженности электрического поля. Теорема Остроградского - Гаусса. 4. Работа по перемещению заряда в электрическом поле. Потенциал, разность потенциалов. 5. Связь напряженности электрического поля с разностью потенциалов. 6. Электроемкость, конденсаторы. 7. Энергия электрического поля. 8. Характеристики электрического тока. Закон Ома, закон Джоуля - Ленца. 9. Электродвижущая сила источника тока. 10. Мощность и к. п. д. источника тока. 11. Разветвленные электрические цепи. Правила Кирхгофа. 12. Электрический ток в металлах. Классическая теория электропроводности металлов. Контактные явления в металлах. 13. Электрический ток в жидкостях, газах и вакууме. Контрольная работа № 2 Электромагнетизм
Таблица вариантов (номер варианта определяется по последней цифре в шифре зачётной книжки) Таблица 7
Перед решением задач данной контрольной работы необходимо хорошо изучить соответствующие темы курса общей физики, указанные в следующей таблице. Таблица 8
401. По двум бесконечно длинным тонким прямым параллельным проводникам текут токи I 1 = 20 А и I 2 = 30 А в одном направлении. Расстояние между проводниками d == 10 см. Вычислите магнитную индукцию В в точке, удаленной от обоих проводников на одинаковое расстояние r = 10 см. 402. Тонкий бесконечно длинный прямой провод согнут под прямым углом. По проводу течет ток I = 100 А. Вычислите магнитную индукцию В в точках, лежащих на биссектрисе угла и удаленных от вершины угла на расстояние а = 10 см. 403. Радиус тонкого проводящего кольца R = 0,2 м. Определите силу тока I, текущего по кольцу, если известно, что в точке, равноудаленной от всех точек кольца на расстояние r = 0,3 м, индукция однородного магнитного поля B = 20 мкТл. 404. По двум тонким бесконечно длинным прямым параллельным проводникам текут токи I 1 = 10 А и I 2 = 5 А в одном направлении. Расстояние между проводниками d = 30 см. На каком расстоянии r от первого проводника на прямой, проходящей через оба проводника, напряженность Н магнитного поля равна нулю? 405. По тонкому проводу, изогнутому в виде прямоугольника со сторонами длиной а = 30 см и b = 40 см, течет ток I = 60 А. Определите магнитную индукцию В в точке пересечения диагоналей прямоугольника. 406. По тонкому бесконечно длинному прямому проводу течет ток I = 10 А. Определите магнитную индукцию В поля, создаваемого отрезком провода длиной l = 20 см в точке, равноудаленной от концов отрезка и находящейся на расстоянии a = 4 см от его середины. 407. По двум тонким бесконечно длинным прямым параллельным проводам текут токи I 1 = 50 А и I 2 = 100 А в противоположных направлениях. Расстояние между проводами d = 20 см. Определите магнитную индукцию В в точке, удаленной на расстояние r 1 == 25 см от первого и на расстояние r 2 = 40 см от второго провода. 408. В центре кругового витка с током радиусом R = 8 см напряженность однородного магнитного поля Н o = 30 А/м. Определите напряженность Н однородного магнитного поля на оси этого витка в точке, расположенной на расстоянии h = 6 см от его центра. 409. Круговой виток радиусом R = 30 см расположен относительно тонкого бесконечно длинного прямолинейного провода так, что его плоскость параллельна проводу. Перпендикуляр, восстановленный на провод из центра витка, является нормалью к плоскости витка. Рас
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 304; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.144.162 (0.018 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

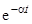 , где начальная сила тока I o = 10 А, коэффициент a = 500 с-1, e - основание натуральных логарифмов. Определите количество теплоты Q, которая выделится в резисторе сопротивлением R = 5 Ом после выключения источника тока.
, где начальная сила тока I o = 10 А, коэффициент a = 500 с-1, e - основание натуральных логарифмов. Определите количество теплоты Q, которая выделится в резисторе сопротивлением R = 5 Ом после выключения источника тока.