
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные теоретические сведенияСодержание книги
Поиск на нашем сайте
Трехфазный источник питания Трехфазная электрическая цепь может быть представлена как совокупность трех однофазных цепей, в которых действуют ЭДС одной и той же частоты, сдвинутые друг относительно друга на одну треть периода, или, что то же, на угол На рис. 1 схематично показана трехфазная цепь, фазы которой электрически не связаны друг с другом. Такие трехфазные цепи называются несвязанными (в настоящее время не применяются).
Рис. 1. Несвязанная трехфазная цепь.
Таким образом, термином «фаза» в электротехнике обозначаются два понятия: угол, определяющий стадию периодического процесса, и составная часть многофазной цепи. Фазы А, В и С изображены на рис. 1 под углом 120° для того чтобы подчеркнуть, что ЭДС
Рис. 2. Связанная электрическая цепь.
В результате этого достигается экономия материала проводов; кроме того, по сравнению с несвязанной трехфазной цепью исключаются потери мощности от токов Трехфазная цепь на рис. 2, фазы которой соединены электрически, представляет собой одну из разновидностей связанных трехфазных цепей. Для получения связанной трехфазной цепи не требуются отдельные однофазные генераторы, а используется трехфазный генератор, схематически показанный на рис. 3.
Рис. 3. Принцип выполнения трехфазного синхронного генератора.
Обмотки, в которых наводятся ЭДС, помешаются в пазах статора. Обмотки фаз сдвинуты друг относительно друга на угол
При вращении ротора, в силу идентичности трех обмоток генератора в них наводятся ЭДС, имеющие одинаковые амплитуду и частоту, причем эти ЭДС сдвинуты по фазе по отношению друг к другу на одну треть периода, рис. 4, а. Векторы, изображающие эти ЭДС, равны по модулю и расположены под углом 120°, рис. 4, б.
Рис. 4. Мгновенные ЭДС (а) и векторная диаграмма ЭДС (б) трехфазного генератора.
Мгновенные ЭДС трехфазного генератора, показанные на рис. 4, а, выражаются аналитически следующим образом:
1.2. Способы соединения фаз генератора и нагрузки Каждая фазная обмотка имеет две крайние точки или два вывода, которые условно называются началом и концом обмотки. За начало обмотки генератора обычно принимается тот вывод, к которому направлена положительная ЭДС. На рис. 2 одноименные выводы фазных обмоток генератора обозначены буквами н (начало) и к (конец). Показанное на схеме рис. 2 соединение обмоток трехфазного генератора называется звездой: все концы фазных обмоток генератора соединены в одной общей точке. Иногда для упрощения рисунка фазы генератора изображают не под углом 120°, а параллельно, рис. 5, а.
Рис. 5. Соединение трехфазного генератора звездой, а – схема; б – векторная диаграмма ЭДС. Общая точка фазных обмоток генератора называется нейтральной точкой. В зависимости от требований нейтральная точка может быть выведена к отдельному выводу, обозначенному на рис. 5, а буквой N. При соединении обмоток трехфазного генератора треугольником, рис. 6, а, начало одной фазной обмотки соединяется с концом следующей по порядку фазной обмотки так, что все три обмотки образуют замкнутый треугольник, причем направления ЭДС в контуре треугольника совпадают и сумма ЭДС равна нулю. Общие точки соединенных обмоток генератора выводятся к выводам, к которым присоединяются линейные провода или нагрузка. При отсутствии нагрузки, т.е. при режиме холостого хода в обмотках генератора, соединенных треугольником, ток не циркулирует, так как сумма трех фазных ЭДС равна нулю, рис. 6, б.
Рис. 6. Соединение трехфазного генератора треугольником, а – схема; б – векторная диаграмма ЭДС.
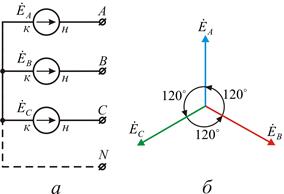
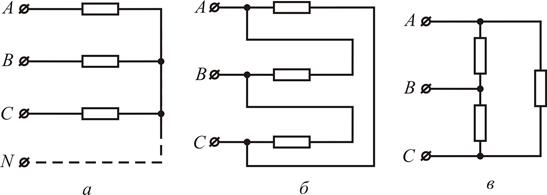
Нагрузка в трехфазной цепи также может быть соединена звездой, рис. 7, а,или треугольником, рис. 7, б и в.
Рис. 7. Соединение нагрузки звездой (а) и треугольником (б и в).
На практике применяются различные комбинации соединении, например: 1) генератор может быть соединен звездой, а нагрузка – звездой или треугольником; 2) генератор может быть соединен треугольником, а нагрузка – звездой или треугольником. Соединение нагрузки звездой без нейтрального провода (рис. 2) применяется только при одинаковой нагрузке всех трех фаз. Между тем условие равномерной загрузки фаз на практике не всегда выполняется (например, в случае осветительной нагрузки). При неравномерной нагрузке напряжения на фазах, т. е. на сопротивлениях лучей звезды нагрузки, получаются неодинаковыми. Кроме того, в схеме рис. 2 недопустимым является включение или отключение одной фазы нагрузки. В этом отношении соединение нагрузки треугольником имеет преимущество: сопротивления фаз, т. е. сторон треугольника, могут быть неодинаковы и даже, в крайнем случае, могут включаться и отключаться независимо друг от друга. Такая же возможность имеется при соединении генератора и нагрузки звездой, если их нейтральные точки соединены нейтральным проводом или через землю (рис. 8, а и б).
Рис. 8. Соединение звезда – звезда с нейтральный проводом (а) и заземленными нейтральными точками (б).
Электродвижущие силы, наводимые в фазных обмотках генератора, напряжения на их выводах, напряжения на фазах нагрузки и токи в них называются соответственно фазными ЭДС, напряжениями и токами и обозначаются Напряжения между линейными проводами и токи в них называются линейными напряжениями и токами и обозначаются При соединении фаз звездой фазные токи равны линейным токам: Различают симметричный и несимметричный режимы работы трехфазной цепи. При симметричном режиме комплексные сопротивления всех трех фаз одинаковы и ЭДС образуют симметричную систему; в противном случае имеет место несимметричный режим. 1.3. Симметричный режим работы трехфазной цепи Введем фазовый оператор
Умножение вектора на оператор а означает поворот вектора на 120° в положительном направлении (против хода часовой стрелки). Соответственно умножение вектора на множитель Очевидно, что
Если ЭДС фазы А равна
В простейшем случае симметричного режима работы трехфазной цепи, когда генератор и активно-индуктивная нагрузка соединены звездой, рис. 9, а, векторная диаграмма имеет вид, показанный на рис. 9, б. Ток в каждой фазе отстает от ЭДС той же фазы на угол
Рис. 9. Симметричный режим работы трехфазной цепи при соединении звездой, а – трехфазная цепь; б – векторная диаграмма.
Токи в фазах при наличии нейтрального провода:
Наличие нейтрального провода не вносит при симметричном режиме никаких изменений, так как сумма токов трех фаз равна нулю и ток в нем отсутствует:
Линейные напряжения определяются как разности соответствующих фазных напряжений:
т. е.
Из треугольника АО D имеем:
В случае соединения треугольником, рис. 10, линейные токи определяются в соответствии с первым законом Кирхгофа как разности фазных токов:
причем
Рис. 10. Симметричный режим работы трехфазной цепи при соединении треугольником, а – трехфазная цепь; б – векторная диаграмма.
Активная мощность симметричной трехфазной нагрузки равна:
Ввиду того что при соединении нагрузки звездой
здесь Аналогичным образом для реактивной и полной мощностей симметричной трехфазной нагрузки имеем:
Если нейтральная точка симметричной трехфазной нагрузки выведена, то измерение активной мощности может быть осуществлено одним ваттметром, включенным по схеме рис. 11, а (одноименные выводы последовательной и параллельной цепей ваттметра отмечены на рис. 11, а звездочками). Утроенное показание ваттметра равно суммарной активной мощности трех фаз.
Рис. 11. Измерение активной мощности при симметричном режиме.
Если нейтральная точка не выведена или нагрузка соединена треугольником, то можно воспользоваться схемой рис. 11, б, где параллельная цепь ваттметра и два добавочных активных сопротивления 1.4. Несимметричный режим работы трехфазной цепи Несимметрия в трехфазной цепи может быть вызвана различными причинами: 1) неодинаковым сопротивлением фаз (несимметричная нагрузка); 2) несимметричным коротким замыканием (например, между двумя фазами или фазой и нейтралью); 3) размыканием фазы; 4) неравенством ЭДС и т.п. Расчет токов и напряжений в трехфазной цепи при несимметричном режиме может производиться теми же методами, которые применяются для расчета однофазных цепей. Рассмотрим несколько вариантов. Несимметричная трехфазная цепь, соединенная звездой, с нейтральным проводом, рис. 12.
Рис. 12. Несимметричная трехфазная цепь, соединенная звездой с нейтральным проводом.
Поскольку в схеме имеются только два узла, целесообразно в данном случае определить узловое напряжение (напряжение смещения) между нейтральными точками O ' и O по формуле:
где
После этого найдем токи:
В симметричной трехфазной цепи Случаю размыкания какой-либо фазы или нейтрального провода соответствует равенство нулю проводимости данной фазы или нейтрального провода. При отсутствии нейтрального провода, полагая в (1)
2. Несимметричная трехфазная нагрузка, соединенная звездой (без нейтрального провода), с заданными линейными напряжениями на выводах, рис. 13.
Рис. 13. Несимметричная трехфазная цепь, соединенная звездой без нейтрального провода.
Если заданы линейные напряжения Обозначив фазные напряжения на выводах нагрузки через
где Равенство нулю суммы токов трех фаз записывается в виде: Фазные напряжения
Подстановка (2) в (3) дает:
Круговой заменой индексов (с порядком следования АВСА и т.д.) находятся:
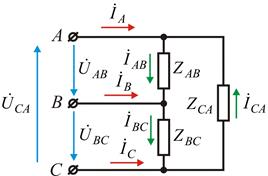
По фазным напряжениям нагрузки находятся фазные токи. 3. Несимметричная трехфазная нагрузка, соединенная треугольником, с заданными напряжениями на выводах, рис. 14.
Рис. 14. Несимметричная трехфазная цепь, соединенная треугольником.
Если на выводах несимметричной трехфазной нагрузки, соединенной треугольником, заданы линейные напряжения
Токи в линии определяются как разности соответствующих токов нагрузки:
Если на выводах несимметричной трехфазной нагрузки, соединенной треугольником, заданы фазные напряжения 1.5. Мощность несимметричной трехфазной цепи Пользуясь комплексной формой записи мощности, можно написать общее выражение для мощности трехфазной цепи:
Действительная часть этого выражения представляет собой активную мощность
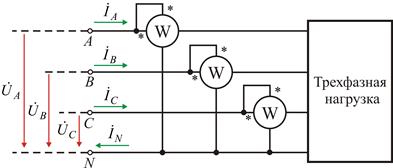
В соответствии с этим выражением, суммарная активная мощность, потребляемая несимметричной трехфазной цепью, может быть измерена при помощи трех ваттметров, включенных на подведенные к данной цепи фазные напряжения и одноименные с ними токи. Активная мощность равна сумме показаний трех ваттметров. Такой метод измерения применяется при наличии нейтрального провода, рис. 15, или искусственно созданной нейтральной точки.
Рис. 15. Измерение мощности при наличии нейтрального провода.
В случае отсутствия нейтрального провода измерение может быть произведено с помощью двух ваттметров, рис. 16.
Рис. 16. Измерение мощности двумя ваттметрами (при отсутствии нейтрального провода).
В соответствии с первым законом Кирхгофа, для схемы, рис. 16:
Выражение такого же вида справедливо и для сопряженных токов:
Подставляя (6) в (5), получаем:
В соответствии с (7) при измерении активной мощности двумя ваттметрами к одному из них подводятся напряжение Круговой заменой А, В и С в выражении (7) можно получить выражения для других равноценных вариантов включения двух ваттметров.
ЗАДАНИЯ И ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
|
|||||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 78; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.165.196 (0.013 с.) |

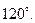 Эти три составные части трехфазной цепи называются фазами и им будут приписываться буквенные обозначения А, В и С.
Эти три составные части трехфазной цепи называются фазами и им будут приписываться буквенные обозначения А, В и С.
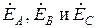 сдвинуты друг относительно друга на одну треть периода. При равенстве амплитуд ЭДС и одинаковых сопротивлениях в фазах токи
сдвинуты друг относительно друга на одну треть периода. При равенстве амплитуд ЭДС и одинаковых сопротивлениях в фазах токи 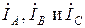 также равны по величине и сдвинуты друг относительно друга на одну треть периода, образуя так называемый трехфазный ток. Сумма этих токов в любой момент времени равна нулю, поэтому если три провода, по которым токи возвращаются к источникам, объединить в один провод, то ток в этом проводе будет равен нулю. При отсутствии в проводе тока излишним в данном случае является и сам провод; от него можно отказаться, перейдя, таким образом, к схеме рис. 2.
также равны по величине и сдвинуты друг относительно друга на одну треть периода, образуя так называемый трехфазный ток. Сумма этих токов в любой момент времени равна нулю, поэтому если три провода, по которым токи возвращаются к источникам, объединить в один провод, то ток в этом проводе будет равен нулю. При отсутствии в проводе тока излишним в данном случае является и сам провод; от него можно отказаться, перейдя, таким образом, к схеме рис. 2.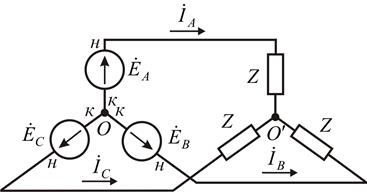
 в обратных проводах.
в обратных проводах.
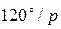 , где р – число пар полюсов. В случае двухполюсного генератора, рис. 3, р =1 и угол равен 120°.
, где р – число пар полюсов. В случае двухполюсного генератора, рис. 3, р =1 и угол равен 120°.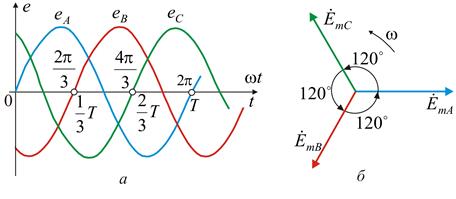



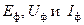 .
.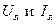 .
. . При соединении фаз треугольником фазное напряжение равно соответствующему линейному напряжению:
. При соединении фаз треугольником фазное напряжение равно соответствующему линейному напряжению: 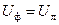 .
.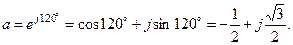
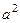 означает поворот вектора на 240° в положительном направлении или, что то же, поворот его на 120° в отрицательном направлении.
означает поворот вектора на 240° в положительном направлении или, что то же, поворот его на 120° в отрицательном направлении.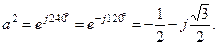
 , то ЭДС фаз В и С равны соответственно:
, то ЭДС фаз В и С равны соответственно:
 где r и х – активное и реактивное сопротивления фаз.
где r и х – активное и реактивное сопротивления фаз.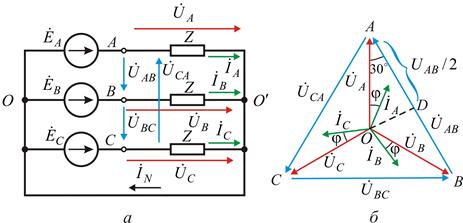
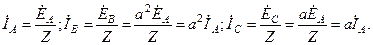
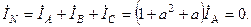
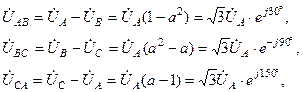
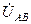 опережает по фазе
опережает по фазе  на 30°, причем модуль
на 30°, причем модуль 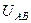 в
в  раз превышает
раз превышает 




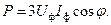
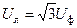 и
и  , а при соединении нагрузки треугольником
, а при соединении нагрузки треугольником 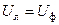 и
и  , активная мощность трехфазной цепи независимо от вида соединения выражается через линейные напряжения и ток следующим образом:
, активная мощность трехфазной цепи независимо от вида соединения выражается через линейные напряжения и ток следующим образом: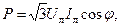
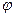 - угол сдвига фазного тока относительно одноименного фазного напряжения.
- угол сдвига фазного тока относительно одноименного фазного напряжения.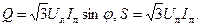
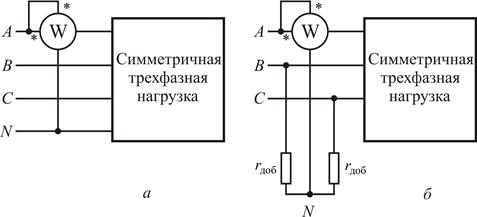
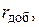 равные по величине сопротивлению параллельной цепи ваттметра, образуют искусственную нейтральную точку 0.
равные по величине сопротивлению параллельной цепи ваттметра, образуют искусственную нейтральную точку 0.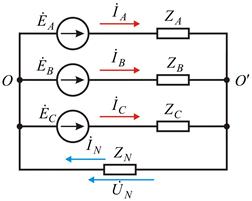
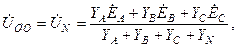 (1)
(1) - проводимости соответствующих ветвей.
- проводимости соответствующих ветвей.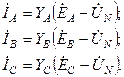
 , и поэтому при
, и поэтому при 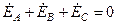 узловое напряжение
узловое напряжение  равно нулю.
равно нулю.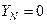 , имеем:
, имеем: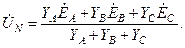
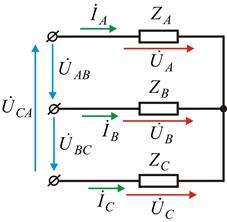
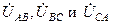 на выводах нагрузки, соединенной звездой, то токи в фазах звезды определяются следующим образом.
на выводах нагрузки, соединенной звездой, то токи в фазах звезды определяются следующим образом.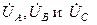 , рис. 13, получим
, рис. 13, получим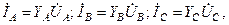
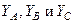 - проводимости фаз нагрузки.
- проводимости фаз нагрузки.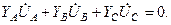 (2)
(2) могут быть выражены через
могут быть выражены через 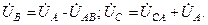 (3)
(3)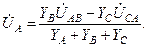
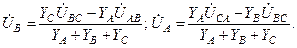 (4)
(4)


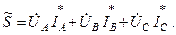 (5)
(5)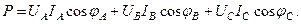

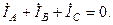
 (6)
(6)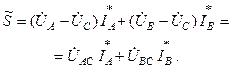 (7)
(7) и ток
и ток 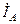 , а ко второму – напряжение
, а ко второму – напряжение 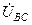 и ток
и ток 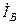 , рис. 16. Показания ваттметров складываются алгебраически.
, рис. 16. Показания ваттметров складываются алгебраически.


