
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эйлеровы и гамильтоновы графы
1. Эйлеровы графы Путь в графе называется эйлеровым, если он содержит все ребра графа. Замкнутый эйлеров путь называется эйлеровым циклом. Граф, который имеет эйлеров цикл, также называется эйлеровым.
Доказательство. Необходимость. Эйлеров цикл, проходя через каждую вершину, выходит из нее столько раз сколько входит. Поэтому число ребер цикла, инцидентное каждой вершине является четным. А так как других ребер в графе, кроме принадлежащих эйлерову циклу, не существует, то степени всех вершин четные. Достаточность. Пусть степени всех вершин четные. Выбрав произвольную вершину v 1, начнем строить из нее цикл. Выйдем из v 1 по любому ребру к следующей вершине v 2. Поскольку степень v 2 четная, то существует другое (не пройденное) ребро, по которому можно перейти к следующей вершине v 3. Поскольку и степень v3 четная, то из v3 так же можно выйти по еще не пройденному ребру и т. д. Будем продолжать этот путь до тех пор, пока это возможно. Заметим, что если вычеркивать пройденные ребра, то степени проходимых вершин уменьшаются на 2 и остаются четными. Поэтому если даже в процессе построения пути мы попадем в вершину, которую уже проходили, найдется не пройденное ребро, по которому можно из этой вершины выйти. Следовательно, данный процесс может закончиться только тогда, когда мы вернемся в исходную вершину v 1 и все ребра, инцидентные v 1, уже будут пройдены. Таким образом, будет получен цикл. Обозначим его через С 1. Если цикл C 1 содержит все ребра графа, то он является искомым. В противном случае, удалим из графа все ребра цикла С 1. В полученном подграфе, как и в исходном, степени всех вершин останутся четными (т. к. либо не изменяется, либо уменьшается на четное число). Удалим также изолированные вершины и обозначим подграф через G 1. Существуют общие вершины у G 1 и построенного цикла С 1 (иначе бы исходный граф не был бы связным). Пусть w 1 – одна из таких вершин. Начав с w 1 точно также, как и раньше, построим цикл С 2 в графе G 1.
содержать все ребра Gn -1. Добавляя С n к циклу, полученному на предыдущем этапе, получим эйлеров цикл. Замечание 1. Теорема справедлива также для мульти- и псевдографов. Замечание 2. Связный граф эйлеров тогда и только тогда, когда существует разбиение множества его ребер Е (G) на простые циклы. Замечание 3. Если в связном графе существует ровно две вершины нечетной степени, то эйлерова цикла не существует, но существует эйлерова цепь, которая начинается в одной вершине нечетной степени, а заканчивается – в другой (доказательство аналогично доказательству теоремы Эйлера). Если число вершин нечетной степени равно 2 k, то нетрудно показать, что граф покрывается (т. е. является обьединением) k реберно-непересекающихся цепями. Ориентированный граф называется эйлеровым, если в нем существует ориентированный эйлеров цикл, т. е. цикл, проходящий по всем дугам с соблюдением ориентации. Легко видеть, что для ориентированных графов, справедлива
deg+ v = deg- v.
2. Гамильтоновы графы Путь (цикл) в графе называется гамильтоновым, если он содержит каждую вершину графа, причем ровно один раз. Граф называется гамильтоновым, если он имеет гамильтонов цикл.
двусвязен. Однако, двусвязности недостаточно, чтобы граф был гамильтоновым (см. рис. 12.2). Простого критерия для определения, является ли граф гамильтоновым или нет (как, например, для определения эйлеровости графа) не существует. Всё же понятно, что чем больше ребер в графе, чем больше степени вершин графа, тем более вероятно ожидать, что граф является гамильтоновым. В частности, полный граф Кn при n ³ 3 очевидно является гамильтоновым. В то же время, существуют гамильтоновы графы и с небольшим числом рёбер, например, циклы Сn, n ³ 3.
Известны следующие достаточные (но не необходимые!) условия гамильтоновости.
графа G её порядок deg v ³ n /2, то G является гамильтоновым. Обобщением этого утверждения является
n ³ 3 сумма их степеней deg v + deg u ³ n, то G гамильтонов. Ориентированный граф называется гамильтоновым, если он имеет ориентированный гамильтонов цикл. Орграф называется турниром, если в нём любая пара вершин соединена одной дугой (со стрелкой в одну сторону). Другими словами, турнир – это некоторая ориентация полного графа.
Задача о коммивояжере Имеется полный взвешенный граф. Требуется отыскать гамильтонов цикл минимального веса. К данной формулировке можно свести и задачу отыскания гамильтонового цикла в неполном графе. В этом случае отсутствующим ребрам присваивают вес ¥. Если нужно найти гамильтонов цикл в обычном (не взвешенном графе), то рёбрам присваивают вес 0, а отсутствующим рёбрам вес ¥ и ищут гамильтонов цикл веса 0. Существуют специальные алгоритмы решения данной задачи. Самый примитивный, но чрезвычайно трудоёмкий, из них – полный перебор. Количество вариантов, которые при этом нужно рассмотреть, равно числу циклических перестановок, т. е. (n -1)!, где n – порядок графа.
Планарные графы
1. Вложимость графов в трехмерное пространство Говорят, что граф вкладывается в данное пространство, если он изоморфен некоторому графу в этом пространстве (все вершины и ребра которого состоят из точек данного пространства), причем кривые, изображающие ребра, не пересекаются.
инцидентные данному ребру (см. рис. 13.1). Понятно, что при этом ребра не могут пересекаться. Рис. 13.1 Замечание. Теорема справедлива также для мульти- и псевдографов. 2. Планарные графы. Формула Эйлера Граф называется планарным, если он может быть уложен на плоскости. Непосредственная укладка планарного графа, т.е. его рисунок, на котором ребра не пересекаются, называется плоским графом. Например, трехмерный куб является планарным графом (см. рис. 13.2), полный граф K 4 также планарный (рис. 13.3).
Ребра плоского графа, образующие простые циклы, разбивают плоскость на несколько частей, которые называются гранями плоского графа. Так, граф куба (см. рис. 13.2) имеет 6 граней (5 внутренних и одну внешнюю), граф K 4 (см. рис. 13.3) имеет 4 грани (3 внутренних и 1 внешнюю). Внешнюю грань имеет всякий планарный граф, даже если в нем нет циклов. Плоский граф вместе со всеми своими вершинами, ребрами, а также гранями называют плоской картой.
равенство (формула Эйлера): n - m + f = 2. Доказательство. Пусть T – остов графа G. T имеет только одну (внешнюю) грань и n -1 ребро, т.е. в этом случае: f = 1, m = n - 1 и очевидно формула справедлива. Будем поочередно добавлять к остову T недостающие ребра графа G. При этом число вершин n не меняется, число ребер m увеличивается на 1. Число граней f также увеличивается на 1. Действительно, если добавленное ребро соединяет две вершины, принадлежащие какому-либо циклу, то грань, ограниченная данным циклом, разбивается на две грани. В противном случае, новая внутренняя грань появляется за счет части внешней грани. В любом случае число граней увеличивается на 1. Таким образом, после добавления каждого ребра формула остается верной. Значит, когда будут восстановлены все ребра и получен граф окажется верной. G, формула также
3. Следствия из формулы Эйлера 1. Число граней любой плоской укладки планарного и равно m - n + 2.
(n, m) -графа G
постоянно Отметим также, что число граней графа G. f = n (G) +1, где n (G) – циклический ранг 2. Пусть выпуклый многогранник имеет В вершин, Р ребер и Г граней. Тогда В - Р + Г = 2. Доказательство. Поместим многогранник внутрь сферы. Выберем некоторую внутреннюю точку O многогранника и проведем через нее всевозможные лучи,
N одной из граней графа на сфере и проведем через диаметрально противоположную точку S касательную плоскость к сфере. Проведя через N всевозможные лучи, отобразим сферу на плоскость (точка N перейдет в бесконечно удаленную точку плоскости). При этом граф со сферы отобразится в некоторый плоский граф на
Рис. 13.4 плоскости. Заметим, что при этом грань, содержащая точку N отобразится во внешнюю грань графа на плоскости . (рис. 13.5). Композиция обоих отображений, α очевидно, определяет биекцию между множествами вершин, ребер, граней данного многогранника и такими же множествами полученного плоского графа. Поэтому полученный граф имеет В вершин, Р ребер и Г граней. Остается воспользоваться формулой Эйлера для графов.
Рис. 13.5 3. Для всякого планарного (n, m) -графа порядка n ³ 3
m £ 3 n - 6. Доказательство. Пусть G – плоский связный (n, m) -граф с f гранями. Всякая грань ограничена не менее, чем 3 ребрами. Всякое ребро либо разграничивает 2 грани, либо ни одной (если не принадлежит ни одному циклу). Поэтому 3 f £ 2 m. По формуле Эйлера неравенство. f = m - n + 2. Поэтому 3 (m - n + 2) £ 2 m, откуда и получаем нужное 4. Граф K 5 не является планарным. Доказательство. Действительно порядок n полного графа K 5 равен 5, а число его ребер m = 10. Если бы этот граф был планарным, то для него выполнялось бы следствие 3, т.е. планарный. 10 £ 3× 5 - 6 Û 10 £ 9, которое не верно. Следовательно, K5 – не 5. Граф K 3,3 не является планарным. Доказательство. Данный граф имеет n = 6 вершин и m = 9 ребер. Предположим, что он планарный. Тогда он имеет f = m - n + 2 = 9 - 6 + 2 = 5 граней. В то же время, всякая грань двудольного графа ограничена четным числом ребер (все циклы имеют четную длину), т.е. не менее, чем четырьмя ребрами. Поэтому 4 f £ 2 m. Но для K 3,3 это неравенство приводит к 4 × 5 £ 2 × 9, что не верно. Значит, предположение о планарности графа K 3,3 ошибочно. 6. В любом простом планарном графе существует вершина степени не более 5. Доказательство. Без потери общности можно считать, что данный граф G – связный планарный (n, m) -граф порядка n ³ 3. Тогда согласно следствию 3 имеем: m £ 3 n - 6. Предположим противное, что степени всех вершин графа G не менее 6. Тогда по лемме о рукопожатиях 6 n £ 2 m, т.е. m ³ 3 n, что противоречит неравенству в следствии 3. Утверждение доказано.
4. Гомеоморфные графы. Критерий планарности Рассмотрим две новые операции на графах. Подразбиением ребра { u, v } графа G называется операция удаления ребра { u, v } с добавлением новой вершины w и двух ребер { u, w } и { w, v }. На рисунке графа G это означает, что добавляется новая вершина w на ребре { u, v }, которое, таким образом, разбивается на два ребра (рис. 13.6). Стягивание смежных вершин u и v графа G означает удаление ребра { u, v } и замена двух вершин u и v одной вершиной, которая соединяется ребрами со всеми вершинами графа G, с которыми были смежны вершины u и v (рис. 13.7).
Графы G и H называются гомеоморфными, если они могут быть получены друг из друга с помощью операций подразбиения ребер и стягивания вершин степени 2 (см. рис. 13.8).
Гомеоморфными являются, в частности, любые две простые цепи, любые два простых цикла.
когда он не содержит подграфов, гомеоморфных K 5 или K 3,3.
подграфов, стягиваемых к графам K 5 или K 3,3. Отметим в заключение, что стягивая любое ребро планарного графа, вновь получим планарный граф. Если же дан непланарный граф, то стянув одно или несколько ребер можно получить планарный граф.
Раскраски графов
1. Хроматическое число графа Раскраска вершин графа G называется правильной, если любые две смежные вершины окрашены в разные цвета. Правильная раскраска графа G, при которой использовано k различных цветов, называется k-раскраской, а граф G, для которого существует k -раскраска, называется k -раскрашиваемым. Наименьшее значение k, для которого существует правильная k -раскраска графа G, называется хроматическим числом графа G и обозначается χ (G) Так, например, для простой цепи Рn хроматическое число равно 2. Хроматическое число простого цикла Сn в случае четного n также равно 2, а для нечетных n – равно 3. В полном графе Кn, очевидно, окраска вершин будет правильной только в случае, если все вершины раскрашены в разные цвета. Поэтому χ (Кn) = n. К поиску правильной окраски графа и его хроматического числа сводится решение многих классических задач.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 945; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.85.33 (0.108 с.) |
 Теорема. (Эйлер). Связный граф является эйлеровым тогда и только тогда, когда степени всех его вершин четные.
Теорема. (Эйлер). Связный граф является эйлеровым тогда и только тогда, когда степени всех его вершин четные.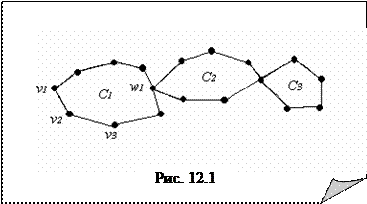 Объединив циклы С 1 и С 2 получим более длинный цикл, чем С 1. Если он содержит все ребра графа, то цель достигнута. В противном случае, снова удалим новый более длинный цикл из исходного графа. В оставшемся подграфе G 2 построим очередной цикл С 3 и т. д. (рис. 12.1). Поскольку число ребер в графе конечное, рано или поздно очередной цикл С n будет
Объединив циклы С 1 и С 2 получим более длинный цикл, чем С 1. Если он содержит все ребра графа, то цель достигнута. В противном случае, снова удалим новый более длинный цикл из исходного графа. В оставшемся подграфе G 2 построим очередной цикл С 3 и т. д. (рис. 12.1). Поскольку число ребер в графе конечное, рано или поздно очередной цикл С n будет Теорема. Связный ориентированный граф является эйлеровым тогда и только тогда, когда для любой его вершины v полустепень исхода равна полстепени захода:
Теорема. Связный ориентированный граф является эйлеровым тогда и только тогда, когда для любой его вершины v полустепень исхода равна полстепени захода: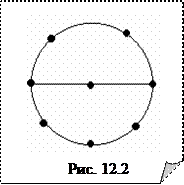 Гамильтоновый граф имеет связность не меньше 2. Действительно, все его вершины принадлежат гамильтонову циклу, который
Гамильтоновый граф имеет связность не меньше 2. Действительно, все его вершины принадлежат гамильтонову циклу, который Теорема (Дирак). Если граф G имеет порядок n ³ 3 и для любой вершины v
Теорема (Дирак). Если граф G имеет порядок n ³ 3 и для любой вершины v Теорема (Оре). Если для любой пары несмежных вершин u и v графа G порядка
Теорема (Оре). Если для любой пары несмежных вершин u и v графа G порядка Теорема. Во всяком турнире порядка n ³ 3 существует гамильтонов путь.
Теорема. Во всяком турнире порядка n ³ 3 существует гамильтонов путь. Теорема. Всякий граф вкладывается в трехмерное евклидово пространство.
Теорема. Всякий граф вкладывается в трехмерное евклидово пространство.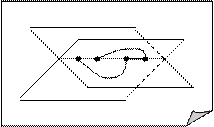 Доказательство. Расположим все вершины данного графа на некоторой прямой. Для каждого ребра (дуги) проведем плоскость через прямую, на которой лежат вершины (для различных ребер – различные плоскости) и соединим соответствующие вершины линией, целиком принадлежащей данной плоскости, так чтобы единственными общими точками данного ребра и прямой были вершины,
Доказательство. Расположим все вершины данного графа на некоторой прямой. Для каждого ребра (дуги) проведем плоскость через прямую, на которой лежат вершины (для различных ребер – различные плоскости) и соединим соответствующие вершины линией, целиком принадлежащей данной плоскости, так чтобы единственными общими точками данного ребра и прямой были вершины,

 Теорема. Для всякого связного плоского (n, m) -графа с f гранями справедливо
Теорема. Для всякого связного плоского (n, m) -графа с f гранями справедливо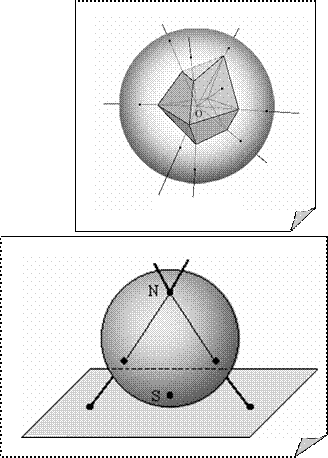 отображая точки поверхности многогранника в точки сферы (см. рис. 13.4). Получим укладку поверхности многогранника на сфере, представляющую собой некоторый граф на сфере. Выберем некоторую внутреннюю точку
отображая точки поверхности многогранника в точки сферы (см. рис. 13.4). Получим укладку поверхности многогранника на сфере, представляющую собой некоторый граф на сфере. Выберем некоторую внутреннюю точку


 Теорема (Понтрягин – Куратовский). Граф планарен тогда и только тогда,
Теорема (Понтрягин – Куратовский). Граф планарен тогда и только тогда, Теорема (Вагнер). Граф планарен тогда и только тогда, когда в нем нет
Теорема (Вагнер). Граф планарен тогда и только тогда, когда в нем нет


