
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Связные графы и расстояние в графах
1. Маршруты в графах. Связные графы Пусть G – мульти- или псевдограф. Последовательность вершин и рёбер вида (n 1, e 1, n 2, e 2, n 3, e 3, ...., e n, n n +1) такая, что e i = { n i, n i +1} – ребро в графе G, соединяющее vi c vi+ 1 называется (v 1, v n + 1) - маршрутом. Вершина v 1 при этом называется началом маршрута, а vn +1 – концом маршрута. Число рёбер n в маршруте называется длиной маршрута. Во взвешенном графе за длину маршрута принимается сумма весов входящих в маршрут рёбер. В простом графе, когда смежные вершины соединены только одним ребром, для задания маршрута достаточно указать только последовательность вершин (разумеется, любые две соседние вершины в этой последовательности должны быть смежными). В этом случае (v 1, v n+ 1 ) – маршрут обозначается: (v 1, v 2, v 3, …, vn+ 1). В маршруте вершины и рёбра могут повторяться. Если в маршруте все рёбра различны, то он называется цепью. Если кроме того в цепи различны и все вершины (кроме, может быть, первой и последней), то такой маршрут называется простой цепью. Маршрут называется циклическим, если в нём начало совпадает с концом. Циклический маршрут являющийся цепью называется циклом, а являющийся простой цепью – простым циклом. Минимальная из длин всех циклов графа называется охватом графа. Граф G называется связным, если в нем для любых двух вершин u и υ существует (u,υ)-маршрут. В ориентированных графах рассматриваются ориентированные маршруты, в которых для любой пары соседних вершин υi и υi+ 1 существует дуга (υi, υi+ 1) (υi – начало дуги, υi+ 1 – конец). Другими словами – это маршруты, по которым можно передвигаться от начала маршрута к концу с соблюдением ориентации (стрелок). Орграф, в котором для любой пары вершин u и υ существуют ориентированные (u, υ)- и (υ, u)-маршруты, называется сильно связным. Если же для любой пары вершин u и υ существует ориентированный (u, υ)- или (υ, u)-маршрут, то такой орграф называется односторонне связным. Орграф в котором любую пару вершин можно соединить маршрутом без соблюдения ориентации (т.е. являющийся связным, если убрать на всех дугах стрелки) называется слабо связным. Легко видеть, что всякий (u, υ)-маршрут содержит (u, υ)-цепь. Для того, что бы её получить, достаточно в маршруте исключить дублирование участков, которые проходятся несколько раз. Кроме того, если из (u, υ)-цепи удалить все промежуточные циклические участки, то получим простую (u, υ)-цепь.
Таким образом, можно дать эквивалентное определение связности: граф называется связным, если в нём любую пару вершин u и υ можно соединить простой (u, υ)-цепью. Для связных графов вводиться также количественная характеристика их связности. Связностью графа G называется наименьшее число вершин, удаление которых приводит к несвязному или тривиальному графу. Так, например, полный граф Kn имеет связность n -1; простая цепь Pn имеет связность 1; простой цикл Сn имеет связность 2; колесо Wn имеет связность 3. Наименьшее число рёбер графа G, удаление которых приводит к несвязному подграфу, называется ребёрной связностью графа G. 2. Компоненты связности. Связность графа и его дополнения Максимальные связные подграфы графа G называются его компонентами связности. Здесь “максимальные” означает: не содержатся в других подграфах с большим числом элементов. На множестве вершин V (G) определим бинарное отношение. Положим v ~ u, если в G существует (v, u)-маршрут. Легко видеть, что это отношение является отношением эквивалентности, причем v ~ u тогда и только тогда, когда вершины v и u содержатся в одной и той же компоненте связности. Таким образом, совокупность компонент связности есть разбиение данного графа (объединение компонент дает весь граф; различные компоненты связности не пересекаются). Граф G ˆ называется графом достижимости графа G (или транзитивным замыкание м графа G), если V (G ˆ) = V (G) и в графе G ˆ вершины v и u соединены ребром тогда и только тогда, когда в G существует (u, υ)-маршрут. Другими словами, в графе G ˆ v и u смежны, если v ~ u в графе G (в смысле отношения эквивалентности, введенного выше).
Понятно, что граф G связен в том и только том случае, когда G ˆ = Kn – полный граф. В случае же, когда G не является связным, G ˆ является объединением нескольких полных подграфов, которые являются его компонентами связности.
3. Расстояния на графах Пусть G – связный граф и u, v – его вершины. Длина кратчайшего (u, v)- маршрута (понятно, что он является простой цепью) называется расстоянием между u и v и обозначается d(u, v). По определению полагают, что d(u, u) = 0 для всякой вершины u. Легко видеть, что отображение d обладает обычными свойствами метрики: 1. d(u, v) ≥ 0, причём d(u, v), только если u=v. 2. d(u, v) = d(v, u). 3. d(u, v) + d(v, w) ≥ d(u, w) (неравенство треугольника). Удалённостью (или, по-другому, эксцентриситетом) вершины v графа G называется наибольшее из расстояний от данной вершины до других вершин графа G: e(v) = max u Î V (G) d(v, u). Радиусом графа G называется наименьшая из удалённостей его вершин: R (G) = min e (v) = v Î V (G) min v Î V (G) max d (v, u). u Î V (G) Диаметром графа G называется наибольшая из удалённостей его вершин: D (G) = max e (v) = v Î V (G) max v Î V (G) max d (v, u). u Î V (G) Вершина v графа G, удалённость которой минимальная (и значит, равна радиусу), называется центром графа G. Точно так же, вершина, удалённость которой максимальная в графе (и значит, равна диаметру), называется периферийным центром. Центр графа не обязательно единственный. Так, например, в полном графе Kn или простом цикле Cn удалённости всех вершин равны, и значит, радиус равен диаметру. Поэтому в этих графах все вершины являются одновременно центрами и периферийными центрами. Задача нахождения центральных вершин графа постоянно возникает в практической деятельности людей. Пусть, например, граф представляет собой сеть дорог, т.е. вершины его соответствуют отдельным населенным пунктам, а ребра – дорогам между ними. Требуется оптимально разместить больницы, магазины, пункты обслуживания. В подобных ситуациях критерий оптимальности часто заключается в оптимизации «наихудшего» случая, т.е. в минимизации расстояния от места обслуживания до наиболее удаленного пункта. Следовательно, местами размещения должны быть центральные вершины. Реальные задачи (их называют минимаксными задачами размещения) отличаются от этой идеальной тем, что приходится еще учитывать другие обстоятельства – фактические расстояния между отдельными пунктами, стоимость, время проезда и прочее. Для того, чтобы учесть это, используют взвешенные графы. Можно показать, что для связного графа G справедливы следующие соотношения: 1. R (G) £ D (G) £ 2 R (G). 2. D (G) ≤ rg G.
4. Метод поиска в ширину Метод поиска в ширину позволяет легко найти расстояние от данной вершины до других вершин графа, и значит, определить удалённость данной вершины. Применив его для всех вершин графа, получим удалённости всех вершин, зная которые, можно найти радиус, диаметр графа, а так же центры и периферийные центры.
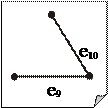
Проиллюстрируем данный метод на следующем примере (см. рис. 10.1).
метку 0. Всем вершинам, смежным с v 1, присвоим метку 1. Затем всем вершинам, смежным с вершинами имеющими метку 1 (которые ещё не имеют метки), присвоим метку 2 и т.д., пока все вершины не получат метки. Легко видеть, что метка вершины будет равна расстоянию от v 1 до данной вершины, а наибольшая из меток равна удалённости вершины v 1. Так, в рассматриваемом примере e(v 1) = 4. Метод позволяет так же находить кратчайшие цепи между вершинами. Если, например, нужно найти кратчайшую цепь от v 1 до v 10, то после расстановки меток двигаемся в обратном порядке от вершины v 10, переходя каждый раз к вершине с меньшей меткой (такая обязательно найдётся; если их несколько, то выбираем любую): v 10 ® v 7 ® v 4 ® v 2 ® v 1. В результате, получаем кратчайшую (v 1, v 10)–цепь: (v 1, v 2, v 4, v 7, v 10). Подсчёты удалённостей остальных вершин в данном приводят к следующим результатам: e(v 2)=3, e(v 3)=3, e(v 4)=3, e(v 5)=3, e(v 6)=3, e(v 7)=3, e(v 8)=3, e(v 9)=4, e(v 10)=4. Таким образом, для данного графа G имеем: R (G)=3; D (G)=4; вершины v 1, v 9, v 10 являются периферийными центрами, а все остальные вершины – центрами.
5. Выяснение вопросов связности, достижимости и расстояний на графе по матрице смежности Пусть G – помеченный граф, V (G) = {1, 2, …, n } и M = (mi,j) – матрица смежности графа G. Умножим матрицу M на себя, т.е. вычислим элементы матрицы M 2
матрицы M 2 в i- той строчке j- том столбце равен: n m (r) = å m m. i, j k =1 i, k k, j Произведения mi,kmk,j будут равны единице только в том случае, когда вершина k является смежной с обеими вершинами i и j, т.е. если существует маршрут длины 2 соединяющий i через k с j. В остальных случаях mi,kmk,j = 0. Поэтому (2)
есть число маршрутов длины 2, соединяющих вершину i с вершиной j. Диагональные элементы матрицы M 2, в частности, совпадают со степенями соответствующих вершин. Точно так же можно показать, что элементы матрицы M 3 суть количества маршрутов длины 3, соединяющие соответствующие пары вершин; элементы M 4 – количества маршрутов длины 4, и т.д. Таким образом, расстояние между вершинами i и j равно наименьшей степени r матрицы M такой, что (i, j)-элемент матрицы Mr отличен от 0. Так как расстояния не могут быть больше n -1, где n – порядок графа, то для того, чтобы найти все расстояния и выяснить другие связанные с ними вопросы, достаточно рассмотреть степени r ≤ n -1.
= 0 для всех 1 ≤ r ≤ n -1, то не существует маршрута между вершинами i и j, и значит, граф не связан.
Деревья и остовы
1. Критерии дерева Деревом называется связный граф без циклов. Произвольный (не обязательно связный) граф без циклов называется лесом. Понятно, что лес состоит из деревьев, которые являются для него компонентами связности.
n ³ 2 имеется по крайней мере две концевые Доказательство. Рассмотрим в дереве простую цепь максимальной длины. Это не цикл, так как в дереве вообще нет циклов. Пусть u и v – начало и конец данной цепи. Тогда u и v – концевые вершины. Действительно, предположим противное, что, например, v не является концевой. Тогда v смежна еще с какой-нибудь вершиной w
(рис. 11.1). Если w принадлежит цепи, то граф имеет цикл, что невозможно, так как он дерево. Если же w не принадлежит цепи, то цепь можно удлинить, добавляя ребро { v, w } и вершину w. А это противоречит тому, что рассматриваемая цепь имеет максимальную длину. Таким образом, утверждение леммы верно.
a) G – дерево; b) любые две различные вершины графа G соединены единственной простой цепью; c) G – граф без циклов, но если любую пару несмежных вершин соединить ребром, то появится ровно один цикл; d) G – связный граф, но перестанет быть связным после удаления любого ребра; e) G – связный граф, причем m = n - 1. Доказательство. а) Þ b). Пусть u и v — две вершины дерева G. По крайней мере одна простая цепь между u и v существует ввиду связности G. Если бы существовала еще хотя бы одна, то объединив их мы получили бы замкнутый маршрут, содержащий цикл, что невозможно, так как G — граф без циклов. b) Þ c). В G нет циклов, иначе бы любые две вершины в цикле были бы соединены по крайней мере двумя простыми цепями (из которых состоит цикл), что противоречит b). Пусть u и v — две несмежные вершины графа G. Согласно b) существует единственная простая получим единственный цикл в G. (u, v)-цепь. Поэтому если провести ребро { u, v }, c) Þ d). G — связный граф, иначе соединив ребром две вершины из разных компонент связности, мы не получили бы цикл, что противоречит с). Удалив любое ребро, мы получим несвязный граф, иначе бы удаленное ребро принадлежало циклу, что также противоречит с). d) Þ e). Достаточно показать, что в G нет циклов. Действительно, если бы был хотя бы один цикл, то удаление любого ребра из цикла нарушило бы связность графа G. Индукция по n. При n = 2 единственным деревом является простая цепь P 2, которая имеет m = 1 ребро, и равенство m = n - 1 очевидно. Предположим, что утверждение d) верно для любого дерева порядка n.
Докажем что тогда оно верно и для дерева порядка n + 1. Рассмотрим такое дерево. Оно содержит концевую вершину (обозначим ее через v), которая существует согласно лемме. Удалим v вместе с инцидентным ей концевым ребром. Полученный граф является деревом порядка n и по индукционному предположению имеет n -1 ребро. Значит, исходное дерево порядка n +1 имело n ребер. Тем самым и для исходного дерева требуемое соотношение верно. e) Þ a). Индукция по n. При n = 2 утверждение а) (то, что G – связный граф без циклов, если в нем две вершины и одно ребро) очевидно. Предположим, что а) верно (при условиях d) для всех графов порядка n. Докажем, что тогда связный граф порядка n + 1, у которого n ребер, также является деревом. Действительно, такой граф имеет концевую вершину. Иначе степени всех вершин были бы ³ 2 и, значит, по лемме о рукопожатиях такой граф содержал бы не менее 2(n + 1) = n + 1
ребер, что противоречит d). Далее, как и в предыдущем случае, удалим концевую вершину и воспользуемся индукционным предположением.
n равно n n -2.
2. Корневое дерево
1 ярусе располагают все вершины дерева, смежные с корнем; затем на 2 ярусе — все вершины, смежные с вершинами 1-го яруса; на 3-ем – вершины, смежные с вершинами 2-го яруса и так далее. Рис. 11.2 Каждому корневому дереву ставится в
подъеме с одного яруса на следующий в код дерева записывается 1, при опускании с яруса на ярус — 0. Так дерево на рисунке имеет код (11101101000011011011000100). Рис. 11.3 Легко видеть, что код дерева обладает следующими свойствами: · длина кода дерева порядка n равна 2(n - 1); · число нулей равно числу единиц; · если обрубить код на каком-либо месте, то число единиц на участке от начала кода до данного места не меньше числа нулей на этом участке (разность между этим количеством совпадает с ярусом, на котором прерван обход). Обратно, по всякому бинарному набору, обладающему этими свойствами, можно построить корневое дерево, код которого совпадает с данным набором. 3. Типы вершин дерева, радиус и центры
полученного подграфа (он также будет деревом) присваивается тип 1. После удаления концевых вершин полученного подграфа, концевым вершинам нового подграфа присваивается тип 2, и так далее пока не будут рассмотрены все вершины (см. рис. 11.4). В конце процесса удаления концевых вершин и присвоения типа новым концевым вершинам, мы получим граф К 1 или К 2. Вершины этого графа (К или К) очевидно 1 2 являются центрами данного дерева. Действительно, их удаленности наименьшие и совпадают с их типом (в случае случае К 1) или на 1 больше типа (в К 2). Таким образом, справедлива следующая теорема.
4. Остовы графа, циклический ранг и ранг разрезов Пусть G – произвольный (n, m) -граф с k компонентами связности. Если G – не лес, то в нем (его компонентах связности) существуют циклы. Рассмотрим какой- либо цикл и удалим из него некоторое ребро. При этом количество компонент связности не увеличится. Если после этого еще останутся циклы, то рассмотрим следующий из них и снова удалим какое-либо его ребро. Продолжим этот процесс до тех пор, пока не исчезнут все циклы. Полученный в результате подграф, который, очевидно, является лесом и имеет столько же компонент связности, как и исходный граф G, называется остовом графа G.
не зависит от способа удаления и равно m - n + k. Доказательство. Пусть H i,
i = 1, k – компоненты связности графа G, и пусть H i - (n i , m i) -графы. После удаления ребер из циклов компоненты H i она превратится в дерево, которое (см. теорему о критериях дерева) имеет n i -1 ребер. Значит, из H i необходимо удалить m i - (n i - 1) ребер. Суммируя по всем компонентам, находим, что для получения остова из графа G необходимо удалить k k k k å(m i - n i + 1) = å m i - å n i + å1 = m - n + k i =1 i =1 i =1 i =1 ребер, что и требовалось доказать. Определение. Число n (G) = m (G) - n (G) + k (G) ребер, которые необходимо удалить из графа G для получения остова, называется циклическим рангом (или цикломатическим числом) графа G. Число ребер в остове графа G, которое в различных остовах одно и то же и равно коциклическим рангом) графа G. n (G) - k (G), называется рангом разрезов (или Легко видеть, что справедливы следующие утверждения: 1. Граф G является лесом тогда и только тогда, когда n (G) = 0. 2. Граф G содержит единственный цикл тогда и только тога, когда n (G) = 1. 3. Граф, в котором число ребер не меньше, чем число вершин, обязательно содержит цикл. Имеют место также следующие теоремы.
порядка n ³ 2 равно алгебраическому дополнению любого элемента матрицы Кирхгофа K (G) графа G.
5. Задача о минимальном остове Задача формулируется следующим образом: во взвешенном связном графе требуется найти остов минимального веса. Данная задача имеет большое практическое значение: проектирование линий электропередачи, трубопроводов, сетей железных дорог и т.д. Существуют достаточно простые алгоритмы решения этой задачи.
Алгоритм Краскала 1 шаг. Строим остовной подграф T 1 = O n È e 1, где O n – пустой граф порядка
  n = G, а e 1 – ребро графа G минимального веса. n = G, а e 1 – ребро графа G минимального веса.
Далее, для i = 2, n -1. 2 шаг. Строим T i = T i -1 È e i, где ребро e i имеет минимальный вес среди ребер, не входящих в T i -1 и не составляющее циклов с ребрами подграфа T i -1. Легко видеть, что граф T n -1 является искомым остовом. Аналогичную структуру имеет и следующий алгоритм. Алгоритм Прима 1 шаг. Строим T 1 = e 1
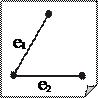
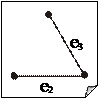
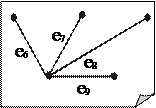
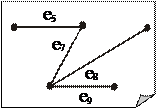
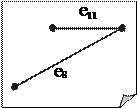
Далее, для i = 2, n - 1. — ребро графа G минимального веса. 2 шаг. Строим T i = T i -1 È e i, где e i – ребро минимального веса, не входящее в T i -1 и инцидентное ровно одной вершине подграфа T i -1. Помимо задачи о минимальном остове рассматривается также задача о максимальном остове, которая формулируется и решается аналогично. 6. Разрезы графа. Фундаментальная система циклов и фундаментальная система разрезов Разделяющим множеством графа G называется такая его совокупность ребер, удаление которых приводит к увеличению числа компонент связности графа G. В частности для связного графа — это такая совокупность ребер графа G, удаление которых приводит к несвязному графу. Минимальное разделяющее множество (то есть такое, что никакое его собственное подмножество разделяющим уже не является) называется разрезом. Разрез, состоящий из одного ребра, называется мостом. Например, для графа, изображенного на рис. 11.5: · множество, но не разрез; · { e 2, e 3 }, { e 5, e 6 }, { e 6, e 7, e 8, e 10 } – разрезы; · { e 4 } – мост; · { e 5, e 7, e 8 } – не является разделяющим множеством. Дополнением подграфа H в графе G будем называть граф
H G, который имеет те же вершины, что и граф G и все те ребра графа G, которые не принадлежат подграфу H.
1. Всякий разрез графа G имеет общее ребро с T.
2. Всякий цикл графа G имеет общее ребро с дополнением T G графе G.
остова T в Доказательство. 1. Пусть множество ребер R графа G является разрезом графа G. Удаление всех ребер множества R разбивает некоторую компоненту связности K графа G на две части K 1 и K 2. Поскольку T – остов, его часть, покрывающая вершины компоненты K, является деревом, в частности, связным графом и поэтому имеет ребро, соединяющее некоторую вершину ребро является общим у R и T. K 1 с некоторой вершиной K 2. Это 2. Пусть теперь C – некоторый цикл графа G. Предположим, что он не имеет общих ребер с
T G. Тогда C целиком содержится в остове T. Но это невозможно, поскольку остов есть лес, то есть граф без циклов. Теорема доказана. Пусть дан граф G. Зафиксируем некоторый его остов T. Как известно (критерии дерева), если добавить к T некоторое ребро графа G (удаленное при получении остова), то появится ровно один цикл. Множество циклов, полученных таким способом, называется фундаментальной системой циклов, ассоциированной с остовом T. Ясно, что все циклы, полученные таким способом, различны и их
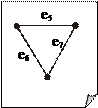
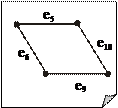
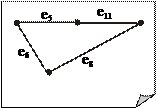
Так, например, если G — граф (рис. 11.5) и T — его остов (рис. 11.6), то фундаментальная система циклов G, ассоциированная с остовом на рис. 11.7 – 11.10. T, представлена
Рис. 11.6
Рис. 11.7 Рис. 11.8 Рис. 11.9 Рис. 11.10
Согласно теореме о критериях дерева (пункт d) удаление любого ребра из остова T разбивает T на две компоненты связности. Пусть V 1 – вершины одной компоненты, а V 2 – другой. Если добавить к такому ребру остова T другие ребра графа G, соединяющие вершины V 1 с вершинами V 2, то получим некоторый разрез графа G. Множество разрезов, полученных таким способом, называется фундаментальной системой разрезов графа G, ассоциированной с остовом T. Понятно, что количество разрезов в фундаментальной системе равно числу ребер в остове, которое совпадает с рангом разрезов графа G. Для рассматриваемого графа G и его остова T, получаем фундаментальную систему разрезов, приведенную на рис. 11.11.
Рис. 11.11
7. Линейное пространство графа Пусть E (G) – множество ребер графа G. Рассмотрим Ù(E (G)) – булеан этого множества, с операцией Å – разностная сумма (или сумма по модулю 2)
следующим образом: " A Í E (G) положим по определению 0 × A = Æ, 1× A = A. Нетрудно убедиться, что эти операции удовлетворяют всем аксиомам линейного пространства: 1. A Å B = B Å A " A, B Í E (G); 2. (A Å B) Å C = A Å (B Å C) " A, B, C Í E (G); 3. существует нулевой элемент – Æ: A Å Æ = A " A Í E (G); 4. для каждого
A Í E (G) существует обратный элемент A:
A Å A = Æ; 5. 1× A = A " A Í E (G); 6. m (nA) = (mn) A " m, n Î Z 2 , " A Í E (G); 7. m (A Å B) = mA Å mB " m Î Z 2 , " A, B Í E (G); 8. (m + n) A = mA + nA " m, n Î Z 2, " A Í E (G). Легко видеть, что базисом этого пространства может служить совокупность одноэлементных подмножеств множества E (G), т.е. совокупность отдельных ребер, и таким образом, размерность векторного пространства графа G равна числу ребер этого графа. Выделим следующие два подпространства этого графа. a) Подпространство циклов: множество всех циклов графа G, включая и совокупности непересекающихся циклов (как одно целое – один элемент линейного пространства), а также – пустое множество (в качестве нулевого элемента). b) Подпространство разрезов: множество разделяющих множеств графа G, включая Æ. Нетрудно убедиться, что операции замкнуты на этих множествах и что они действительно являются подпространствами. Заметим также, что фундаментальные системы циклов и разрезов, соответственно, является базисами этих подпространств.
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 168; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.193.232 (0.396 с.) |
|||||||||||||||||||||||||||||||||||||||||
 Теорема. Всякий граф или его дополнение является связным.
Теорема. Всякий граф или его дополнение является связным.
 Доказательство. Предположим, что G – не связный граф, и докажем, что тогда его дополнение G есть связный граф. Действительно, пусть A – множество вершин какой-либо компоненты связности графа G, а B = V (G)\ A – остальные вершины. Тогда в графе G всякая вершина a Î A соединена ребром с каждой вершиной b Î B. Пусть ai, aj Î A, тогда (ai, b, aj) – маршрут, соединяющий ai с aj (здесь b –любая вершина из B). Аналогично, если bi, bj Î B, то (bi, a, bj) – маршрут соединяющий bi с bj, (a – любая вершина из A). Таким образом, для любых двух вершин в G существует соединяющий их маршрут (длины не более 2), что и требовалось доказать.
Доказательство. Предположим, что G – не связный граф, и докажем, что тогда его дополнение G есть связный граф. Действительно, пусть A – множество вершин какой-либо компоненты связности графа G, а B = V (G)\ A – остальные вершины. Тогда в графе G всякая вершина a Î A соединена ребром с каждой вершиной b Î B. Пусть ai, aj Î A, тогда (ai, b, aj) – маршрут, соединяющий ai с aj (здесь b –любая вершина из B). Аналогично, если bi, bj Î B, то (bi, a, bj) – маршрут соединяющий bi с bj, (a – любая вершина из A). Таким образом, для любых двух вершин в G существует соединяющий их маршрут (длины не более 2), что и требовалось доказать.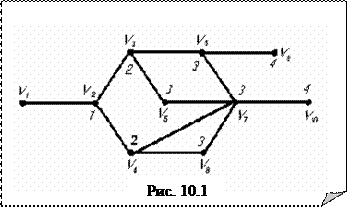 Суть метода заключается в расстановке меток, которая осуществляется по следующему правилу. Предположим, нужно найти расстояние от вершины v 1 до других вершин. Присвоим вершине v 1
Суть метода заключается в расстановке меток, которая осуществляется по следующему правилу. Предположим, нужно найти расстояние от вершины v 1 до других вершин. Присвоим вершине v 1 Лемма. В любом дереве порядка вершины.
Лемма. В любом дереве порядка вершины. помимо v 0 – предыдущей в цепи
помимо v 0 – предыдущей в цепи Теорема. Пусть G – (n, m)-граф. Следующие утверждения равносильны:
Теорема. Пусть G – (n, m)-граф. Следующие утверждения равносильны: 2
2 Теорема (Кэли). Число неизоморфных помеченных деревьев порядка
Теорема (Кэли). Число неизоморфных помеченных деревьев порядка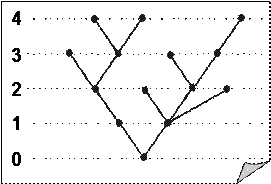 Корневое дерево есть специальный способ представления (изображения) дерева. Выбирается некоторая вершина, которая именуется «корнем дерева». При изображении все вершины располагают по ярусам, следующим образом. На нулевом ярусе располагается корень дерева (см. рис. 11.2). На
Корневое дерево есть специальный способ представления (изображения) дерева. Выбирается некоторая вершина, которая именуется «корнем дерева». При изображении все вершины располагают по ярусам, следующим образом. На нулевом ярусе располагается корень дерева (см. рис. 11.2). На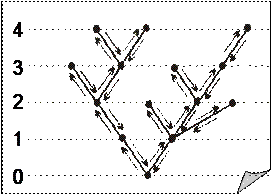 соответствие его бинарный код, который строится в процессе полного обхода дерева. Обход начинается с корня и заканчивается корнем. Обход осуществляется слева направо, т.е. сначала проходится левая ветвь, затем следующая и так далее, в конце — самая правая. При обходе необходимо подниматься по ветви (см. рис. 11.3) до тех пор, пока это возможно. Затем по ветви опускаются до тех пор, пока не появится возможность продолжить подъем по еще не пройденной ветви. При
соответствие его бинарный код, который строится в процессе полного обхода дерева. Обход начинается с корня и заканчивается корнем. Обход осуществляется слева направо, т.е. сначала проходится левая ветвь, затем следующая и так далее, в конце — самая правая. При обходе необходимо подниматься по ветви (см. рис. 11.3) до тех пор, пока это возможно. Затем по ветви опускаются до тех пор, пока не появится возможность продолжить подъем по еще не пройденной ветви. При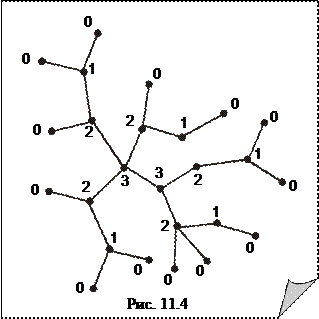 Вершины дерева можно разбить на типы. Всем концевым вершинам присваивается тип 0. Удалим все концевые вершины вместе с инцидентными им ребрами. Всем концевым вершинам
Вершины дерева можно разбить на типы. Всем концевым вершинам присваивается тип 0. Удалим все концевые вершины вместе с инцидентными им ребрами. Всем концевым вершинам Теорема. Существует не более двух центров дерева. Они совпадают с вершинами максимального типа. Радиус дерева R(G) равен r, если центр единственный и его тип r, или r + 1, если центра два и их тип r.
Теорема. Существует не более двух центров дерева. Они совпадают с вершинами максимального типа. Радиус дерева R(G) равен r, если центр единственный и его тип r, или r + 1, если центра два и их тип r. Теорема. Число ребер графа G, которые нужно удалить для получения остова,
Теорема. Число ребер графа G, которые нужно удалить для получения остова,
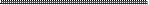 Теорема (Кирхгоф). Число остовов в связном графе G
Теорема (Кирхгоф). Число остовов в связном графе G

 { e 2, e 5, e 7, e 6 } – разделяющее
{ e 2, e 5, e 7, e 6 } – разделяющее
 Теорема. Пусть T – остов графа G.
Теорема. Пусть T – остов графа G.
 количество равно циклическому рангу n (G).
количество равно циклическому рангу n (G).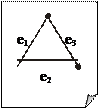


 A Å B = (A I B)U (A I B). Определим также умножение на элементы Z 2 = {0, 1}
A Å B = (A I B)U (A I B). Определим также умножение на элементы Z 2 = {0, 1}




