
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Произвольные выражения векторной алгебрыСодержание книги
Поиск на нашем сайте
f) Вычислить 2 a, b ∙ p +3 b ∙ p 2 - b ∙ b Вычислим отдельно три слагаемых выражения и образуем из них ответ: S1 <- 2*as.numeric(a%*%b)*p # Первое слагаемое S2 <- 3*b*as.numeric(p%*%p) # Второе слагаемое S3 <- norm(b, type="2")*b # Третье слагаемое S1 + S2 - S3 # Ответ c результатом в виде вектора > S1 + S2 - S3[1] -981.4099 302.1149 -702.8199 -940.7050Обратите внимание, что при вычислении скалярных произведений необходимо конвертировать ответ в число с помощью команды as.numeric(), иначе произойдет несовпадение типов (матрицы и векторы как бы перемешаются в одном выражении) и компилятор R выдаст ошибку. Если вычисление скалярных произведений производится для многих пар векторов, то для этих целей удобно запрограммировать специальную пользовательскую функцию, скажем, под названием cosV: cosV <- function(x,y) { # Объявление имени функции cosV двух аргументов L.x <- norm(x, type="2"); L.y <- norm(y, type="2") # Нахождение длин векторов cosV <- x%*%y/(L.x*L.y) # Нахождение косинуса угла return(as.numeric(cosV)) # Возвращение косинуса в качестве значения функции } cosV(a,b) # Вызов пользовательской функции cosV > cosV(a,b) # Вызов пользовательской функции cosV[1] -1
Задания для самостоятельной работы 1. Образовать и вывести на экран векторы a(1,1,2) a) -4a+5b b) 2 a,b *a-3 b *b 2. Образовать и вывести на экран векторы a(2,0,-3) 3. Образовать и вывести на экран векторы a(1,1,2,2,3,3,4,4) b(-2,-1,0,1,2,3,4,5) 4. Выбрать из матрицы A вектор-столбец максимальной длины, если матрица имеет вид: A= 1 0 4 2 3 4 3 1 3 -2 1 1 2 0 -3 2 9 5 4 0 3 5 7 1 6 4 1 2 0 -5 -2 8 3 2 0 2. 5. Есть ли в матрице из предыдущего задания ортогональные столбцы? Если есть, то какие пары? Ответы: 1. а) (-4,-24,7) 1. b) (4,64,-37) 2. |a|=3.605551; |b|=7.28011; (a,b)=0 – да, ортогональны 3. |a|=|b|=7.745967; (a,b)=50; cos(a,b)=0.8333333 >0 – угол острый 4. 5-ый столбец 5. Да, есть ортогональные: 4-ый и 5-ый столбцы
Векторная алгебра (R S tudio) Учебно-методическое пособие
для проведения семинара №27 по дисциплине «Компьютерный практикум»
для студентов, обучающихся по направлениям подготовки 38.03.01 «Экономика» и 38.03.02 «Менеджмент» (программа подготовки бакалавров).
Автор: Конев Александр Евгеньевич, старший преподаватель департамента анализа данных, принятия решений и финансовых технологий
Вычитка и корректура выполнены автором
© ФГОБУ ВО «Финансовый университет при Правительстве Российской Федерации», 2018. © Департамент анализа данных, принятия решений и финансовых технологий, 2018. © Конев Александр Евгеньевич, 2018.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 144; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.7.115 (0.009 с.) |
||||||||||||||||||

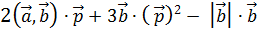
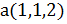 и b(0,-4,3)
и b(0,-4,3) 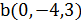 . Вычислить выражение
. Вычислить выражение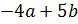
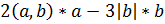
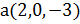 и b(6,1,4)
и b(6,1,4) 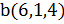 . Вычислить их длины и скалярное произведение. Ортогональны ли векторы?
. Вычислить их длины и скалярное произведение. Ортогональны ли векторы?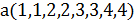 и
и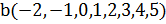 . Какой вектор длиннее? Определить тупой, острый или прямой угол образован между векторами и найти его косинус.
. Какой вектор длиннее? Определить тупой, острый или прямой угол образован между векторами и найти его косинус.



