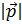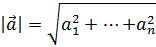Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Скалярное произведение векторов. b) вычислить a ∙ b и a ∙ pСодержание книги
Поиск на нашем сайте
b) вычислить a ∙ b В отличие от предыдущего пункта, здесь нельзя составить обычное умножение векторов, т.к. компилятор R покоординатно перемножит векторы, что не является скалярным произведением. Вообще, важно различать покоординатное произведение векторов (не используется в векторной алгебре, но удобно в программировании): a 1 b 1; a 2 b 2;…; a n b n и скалярное произведение векторов (то что нам сейчас нужно): a ∙ b = a 1 b 1 + a 2 b 2 +…+ a n b n Как видите, в результате получается не вектор, а число (скаляр) – отсюда и название скалярное произведение. Желая подчеркнуть эту разницу в линейной алгебре часто используют круглые скобки для обозначения скалярного произведения: a ∙ b = a; b. В языке R эти два приёма программируется следующим образом: a*b # Покоординатное произведение векторов (не скалярное произведение!) a%*%b # Скалярное произведение векторов с результатом: > a*b # Покоординатное произведение векторов (не скалярное произведение!)[1] -12 -27 -48 -3> a%*%b # Скалярное произведение векторов [,1][1,] -90Обратите внимание, что результат скалярного произведения представлен в виде матрицы 1×1 as.numeric(a%*%b) # Скалярное произведение векторов > as.numeric(a%*%b)[1] -90 Аналогично получим скалярное произведение a ∙ p as.numeric(a%*%p) # Скалярное произведение векторов > as.numeric(a%*%p)[1] 0 Кстати, в последнем случае результат оказался равным нулю, что говорит об ортогональности (перпендикулярности) векторов a Впрочем, для нахождения скалярного произведения мы могли бы использовать простую конструкцию в виде суммы (sum) попарных произведений координат: sum(a*p) # Фактически тоже скалярное произведение векторов с тем же результатом. с) вычислить a 2 = a ∙ a Квадрат вектора a 2 as.numeric(a%*%a) # Квадрат вектора > as.numeric(a%*%a) # Квадрат вектора[1] 30Проверьте, что результат, действительно, равен сумме квадратов координат вектора:
a 2 = a ∙ a = a 1 a 1 + a 2 a 2 +…+ a n a n = a 1 2 +… +a n 2 Замечание. Ошибкой было бы записать a*a или a^2, т.к. в этом случае R выдал бы покоординатное выполнение указанных операций, а не их сумму: (a 1 2,…,a n 2) Длина вектора d) вычислить a Длиной вектора называют число, равное квадратному корню из a 2 a = a 1 2 +… +a n 2 В языке R получить данное выражение можно несколькими способами. Первый из них – вызвать специальную функцию вычисления нормы элемента для вектора: norm(a, type="2") # Длина вектора a (обычная евклидова) с результатом: > norm(a, type="2") # Длина вектора a (обычная евклидова)[1] 5.477226Второй способ – образовать, согласно формуле, корень из суммы квадратов элементов: sqrt(sum(a^2)) # Альтернатива: длина вектора a с тем же результатом: > sqrt(sum(a^2)) # Альтернатива: длина вектора a[1] 5.477226Аналогично получаем для оставшихся векторов: norm(b, type="2") # Длина вектора b (обычная евклидова) sqrt(sum(p^2)) # Альтернатива: длина вектора p
|
|||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 109; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.21.145 (0.008 с.) |

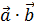 и a ∙ p
и a ∙ p 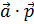
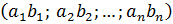
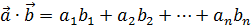 .
.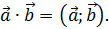
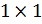 , т.к. в языке R эта операция интерпретируется как частный случай произведения специальных матриц. Если мы не хотим видеть результат в виде матрицы, мы можем вывести его как обычное число:
, т.к. в языке R эта операция интерпретируется как частный случай произведения специальных матриц. Если мы не хотим видеть результат в виде матрицы, мы можем вывести его как обычное число: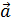 и p
и p 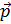 .
.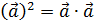
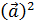 понимается в векторной алгебре как скалярное произведение самого на себя a ∙ a
понимается в векторной алгебре как скалярное произведение самого на себя a ∙ a 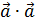 , поэтому легко получить:
, поэтому легко получить: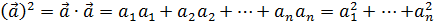
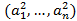 .
.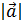 , b
, b 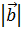 и p
и p