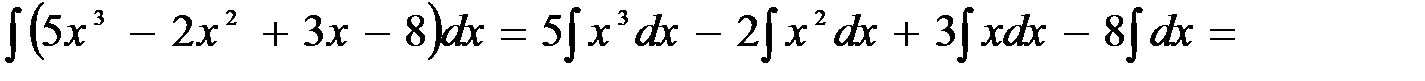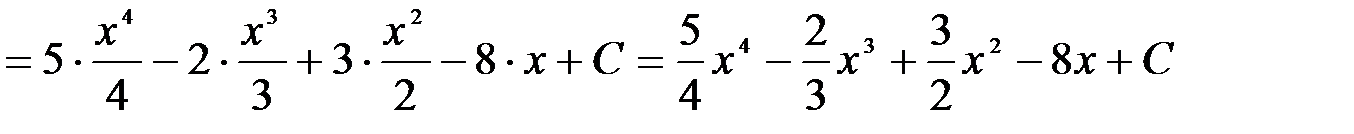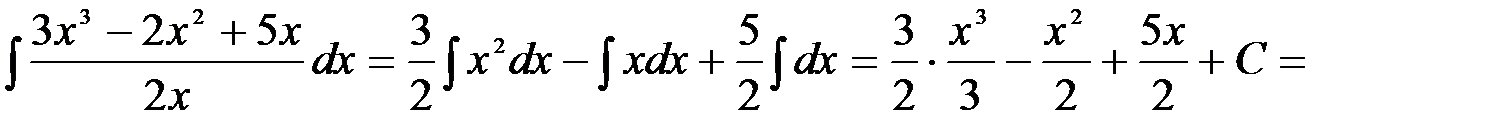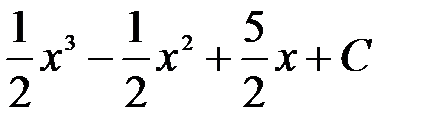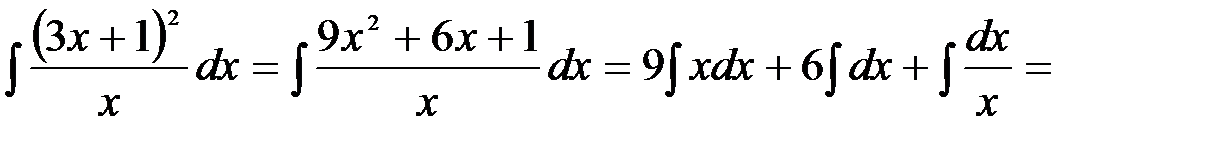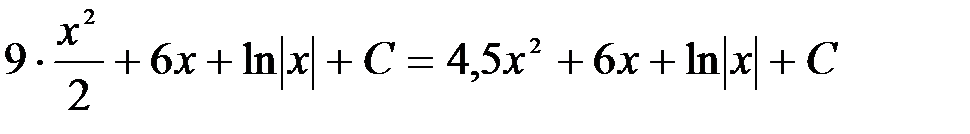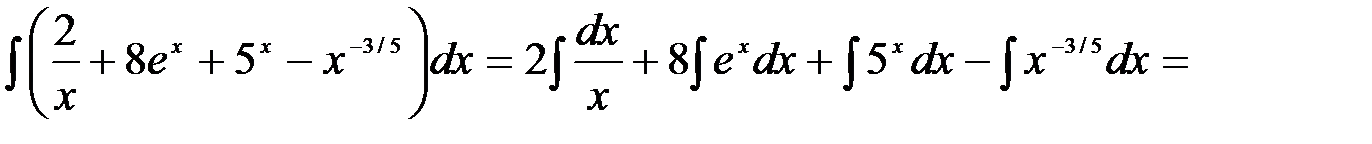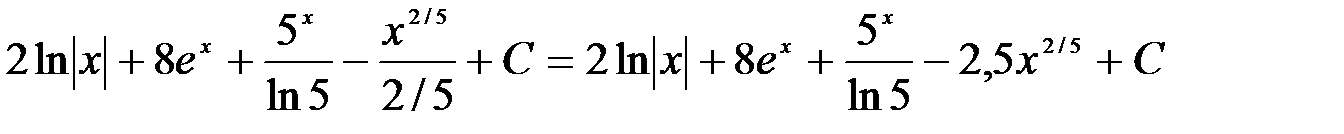Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные свойства неопределенного интегралаСодержание книги
Поиск на нашем сайте
Из рассмотренных ранее примеров видно, что можно находить интегралы, подбирая первообразные. Однако это не всегда просто. При интегрировании помогает знание некоторых свойств интеграла, формул интегрирования, а также специальных приемов. Рассмотрим сначала основные свойства неопределенного интеграла.
Это свойство непосредственно вытекает из определения неопределенного интеграла, поскольку Так, На этом свойстве основано доказательство следующих свойств.
где m – постоянная величина, не равная нулю. Это свойство доказывается дифференцированием обеих частей приведенного равенства. При этом учитывается свойство 1: производная неопределенного интеграла равна подынтегральной функции. Действительно,
Например,
Для доказательства найдем производные обеих частей равенства и покажем, что они равны между собой. Сначала найдем производную левой части:
мы воспользовались свойством 1 неопределенного интеграла. Теперь найдем производную правой части равенства:
Здесь был использован тот факт, что производная алгебраической суммы функций равна алгебраической сумме этих функций, а также свойство 1 неопределенного интеграла. Итак, производные обеих частей равенства равны между собой, что и доказывает свойство 3.
Это свойство следует из определения неопределенного интеграла. Действительно, Например,
Действительно, Например, На основании этого свойства выводятся формулы интегрирования.
Формулы интегрирования Из определения интеграла следует, что для того, чтобы проинтегрировать функцию, нужно найти ее первообразную. Для ряда функций это легко сделать, используя соответствующие формулу интегрирования. Например, мы знаем, что Итак, формулы интегрирования получаются обращением соответствующих формул дифференцирования. Выпишем в таблицу основные интегралы.
Интегралы, приведенные в этой таблице, называются табличными интегралами. Для вывода этих формул, как уже отмечалось, используется свойство 5 неопределенного интеграла, а именно дифференцирование правой части равенства. Производная правой части равенства дает подынтегральную функцию, а дифференциал – подынтегральное выражение. Формула 1 справедлива при любом n, кроме n=-1, так как в этом случае знаменатель обращается в нуль и выражение теряет смысл. Для доказательства найдем производную правой части равенства:
Мы получили подынтегральную функцию; следовательно, формула верна. Случаю n=-1 соответствует формула 2:
В промежутке В промежутке Итак, оба промежутка непрерывности подынтегральной функции объединяются записью Справедливость всех остальных табличных интегралов легко проверить, если продифференцировать их правые части.
Отметим, что формула 3 является частным случаем формулы 4 при
Вычисление интегралов способом приведения их к табличным с помощью преобразования подынтегрального выражения и применения свойств 2 и 3 неопределенного интеграла называется непосредственным интегрированием. При этом полезно запомнить, что 1.
2.
=
3.
=
4. =
|
||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 96; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.126.69 (0.007 с.) |

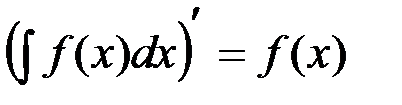
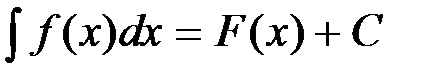 , а
, а 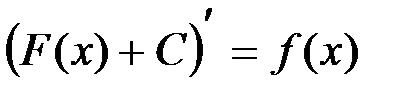 .
.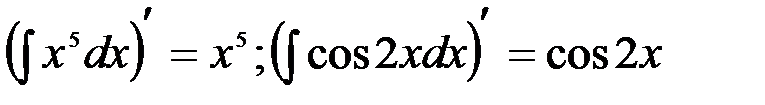 .
.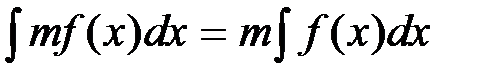 ,
, .
.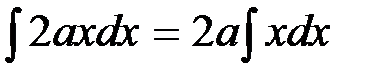 , где а – постоянная, не равная нулю.
, где а – постоянная, не равная нулю.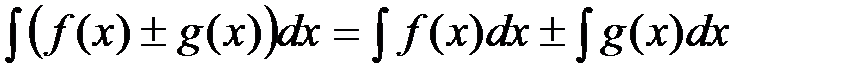
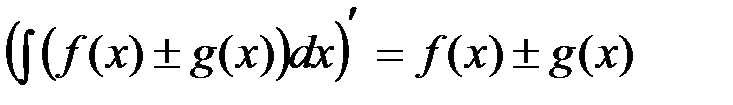
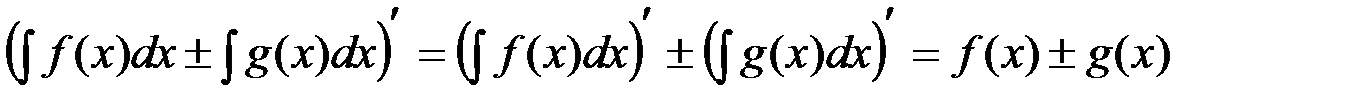 .
.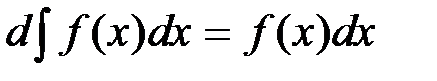 .
.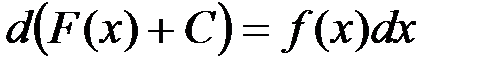 . Свойство 4 означает, что знак дифференциала аннулирует знак интеграла.
. Свойство 4 означает, что знак дифференциала аннулирует знак интеграла.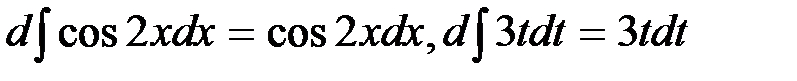 и т.д.
и т.д.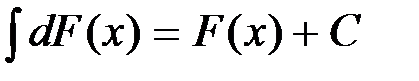 или
или 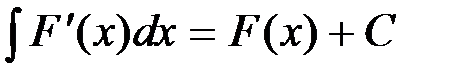 .
.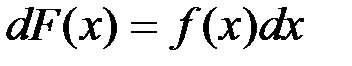 . Возьмем интеграл от обеих частей равенства и получим
. Возьмем интеграл от обеих частей равенства и получим 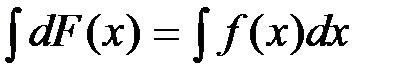 . Но, по определению,
. Но, по определению, 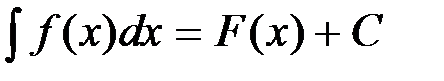 , т.е.
, т.е. 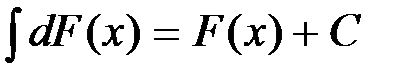 .
.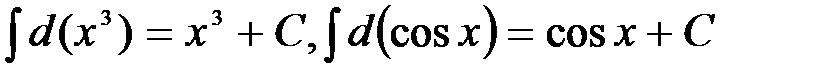 и т.д.
и т.д. ; отсюда следует, что
; отсюда следует, что 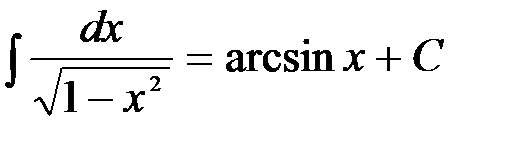 .
.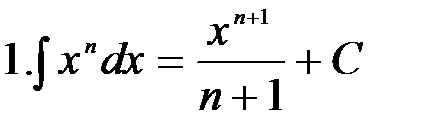 при
при 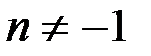
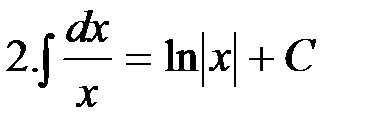
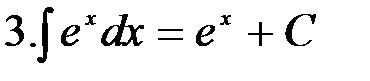
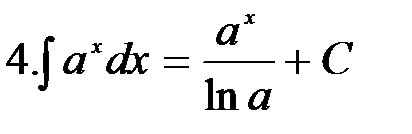
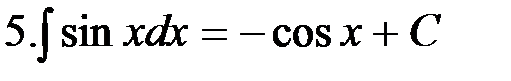
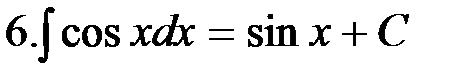
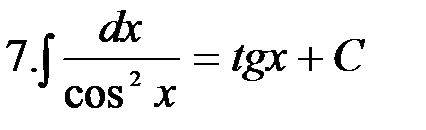
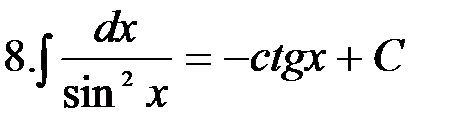
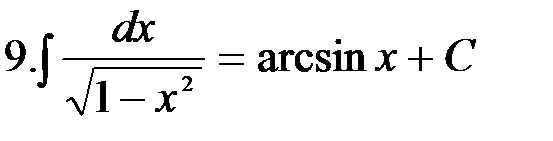
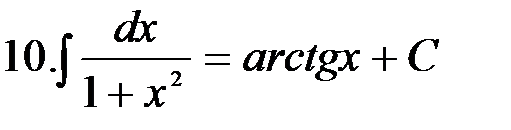
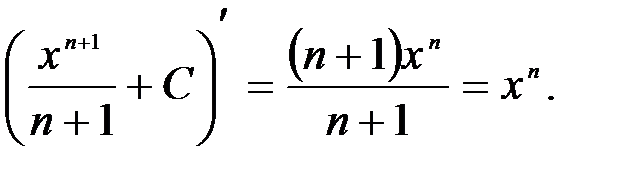
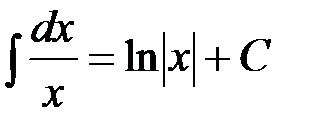
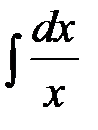 , заметим, что функция
, заметим, что функция 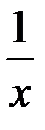 непрерывна в промежутках
непрерывна в промежутках 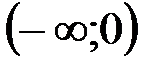 и
и 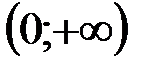 , причем в каждом из них она имеет первообразную.
, причем в каждом из них она имеет первообразную.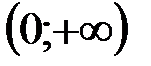 этой первообразной, очевидно, является функция
этой первообразной, очевидно, является функция 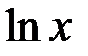 , так как
, так как 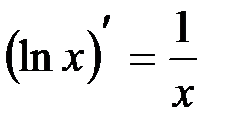 , т.е.
, т.е. 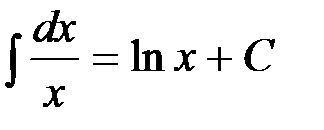 при
при 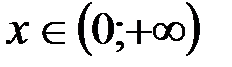 .
.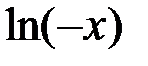 , т.е.
, т.е. 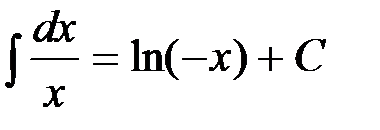 при
при 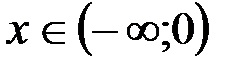 . Действительно,
. Действительно, 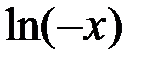 существует при
существует при  и
и 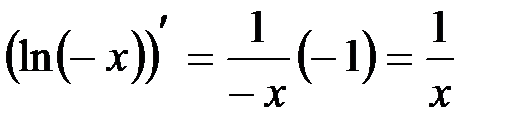 .
.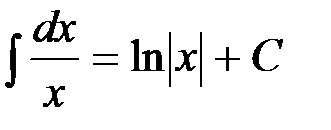 .
.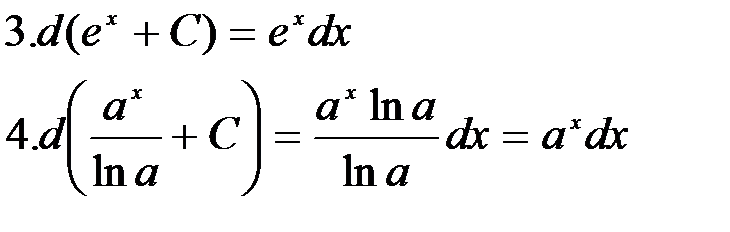
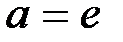 .
.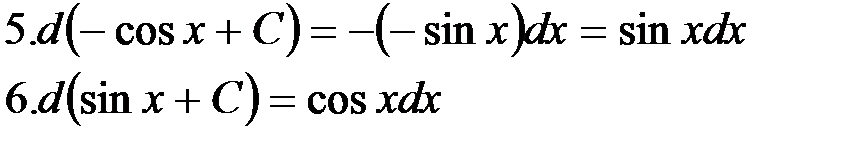
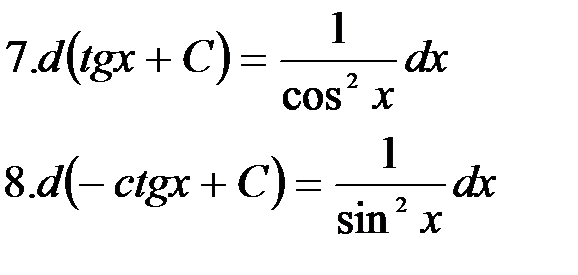
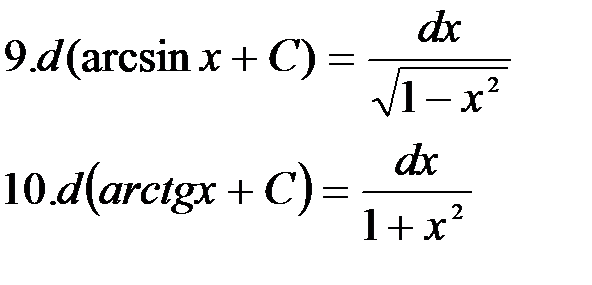
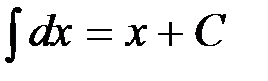 (формула 1 при
(формула 1 при 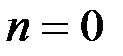 ).
).