
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие первообразной и неопределенного интеграла.Стр 1 из 5Следующая ⇒
Понятие первообразной и неопределенного интеграла. Свойства. Формулы интегрирования. Первообразная Функцию, восстанавливаемую по заданной ее производной или дифференциалу, называют первообразной. Дифференцируемая функция Из этого определения вытекает, что всякая функция по отношению к своей производной является первообразной. Так, функция
Дифференцирование функции – однозначная операция, т.е. если функция имеет производную, то только одну. Это утверждение непосредственно следует из определений предела и производной: если функция имеет предел, то только один. Обратная операция – отыскание первообразной – не однозначна. Так, функции Теорема. Если Доказательство: Пусть Покажем теперь, что все первообразные функции Пусть Ф(х) – другая первообразная функции Тогда Таким образом, любые две первообразные данной функции отличаются друг от друга на постоянное слагаемое, а выражение Геометрически выражение
Неопределенный интеграл Как уже было отмечено, первообразную можно находить не только по данной ее производной, но и по ее дифференциалу. В дальнейшее мы будем этим пользоваться. Определение. Совокупность всех первообразных Таким образом, если Замечание. Наличие постоянной С делает задачу нахождения функции по ее производной не вполне определенной; отсюда происходит название «Неопределенный интеграл». Так, пользуясь определением неопределенного интеграла, можно записать: Значит, чтобы найти неопределенный интеграл от заданной функции, нужно найти какую-нибудь одну из ее первообразных и прибавить к ней произвольную постоянную С. Слово «интеграл» происходит от латинского слова integer, что означает «восстановленный». Интегрируя какую-либо функцию, например Чтобы проверить, правильно ли найден неопределенный интеграл, необходимо продифференцировать полученную функцию, если при этом получается подынтегральное выражение, то интеграл найден верно. Например, Формулы интегрирования Из определения интеграла следует, что для того, чтобы проинтегрировать функцию, нужно найти ее первообразную. Для ряда функций это легко сделать, используя соответствующие формулу интегрирования. Например, мы знаем, что Итак, формулы интегрирования получаются обращением соответствующих формул дифференцирования. Выпишем в таблицу основные интегралы.
Интегралы, приведенные в этой таблице, называются табличными интегралами. Для вывода этих формул, как уже отмечалось, используется свойство 5 неопределенного интеграла, а именно дифференцирование правой части равенства. Производная правой части равенства дает подынтегральную функцию, а дифференциал – подынтегральное выражение.
Формула 1 справедлива при любом n, кроме n=-1, так как в этом случае знаменатель обращается в нуль и выражение теряет смысл. Для доказательства найдем производную правой части равенства:
Мы получили подынтегральную функцию; следовательно, формула верна. Случаю n=-1 соответствует формула 2:
В промежутке В промежутке Итак, оба промежутка непрерывности подынтегральной функции объединяются записью Справедливость всех остальных табличных интегралов легко проверить, если продифференцировать их правые части.
Отметим, что формула 3 является частным случаем формулы 4 при
Вычисление интегралов способом приведения их к табличным с помощью преобразования подынтегрального выражения и применения свойств 2 и 3 неопределенного интеграла называется непосредственным интегрированием. При этом полезно запомнить, что 1.
2.
=
3.
=
4. = Замечания. 1. Под
Все методы интегрирования, используемые при нахождении неопределенных интегралов, применяются и при вычислении определенных интегралов. Числовое значение определенного интеграла зависит от вида функции, стоящей под знаком интеграла, и от значений верхнего и нижнего пределов и не зависит от обозначения переменной. Если формулу Ньютона-Лейбница сравнить с формулой (1), то, очевидно, что Таким образом, если функция Тогда площадь криволинейной трапеции можно вычислить по формуле
Понятие первообразной и неопределенного интеграла.
|
|||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 87; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.190.232 (0.027 с.) |
 называется первообразной для функции
называется первообразной для функции  на заданном промежутке, если для всех х из этого промежутка справедливо равенство
на заданном промежутке, если для всех х из этого промежутка справедливо равенство 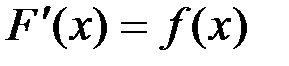 .
. есть первообразная функции
есть первообразная функции  на интервале
на интервале  , поскольку для всех
, поскольку для всех  имеет место равенство
имеет место равенство  .
. .
Решение: Используя правило дифференцирования, можно догадаться, что на интервале
.
Решение: Используя правило дифференцирования, можно догадаться, что на интервале  . Действительно,
. Действительно,  для всех
для всех  .
2. Найти первообразную функции
.
2. Найти первообразную функции  на множестве R.
Решение: Степень
на множестве R.
Решение: Степень  получается при дифференцировании
получается при дифференцировании  . Так как
. Так как  , то, чтобы при дифференцировании
, то, чтобы при дифференцировании  .
.
 , где С – любое постоянное действительное число, являются первообразными функции
, где С – любое постоянное действительное число, являются первообразными функции  , поскольку все эти функции имеют одну и ту же производную
, поскольку все эти функции имеют одну и ту же производную  .
. , где С – любое действительное число.
, где С – любое действительное число. . Тогда
. Тогда  .
.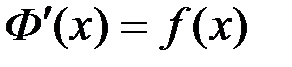 .
. при всех х из рассматриваемого промежутка. Следовательно,
при всех х из рассматриваемого промежутка. Следовательно,  , что и требовалось установить.
, что и требовалось установить. , где
, где  - подынтегральное выражение, х – переменная интегрирования.
- подынтегральное выражение, х – переменная интегрирования.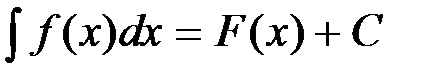 , где С – любое действительное число.
, где С – любое действительное число.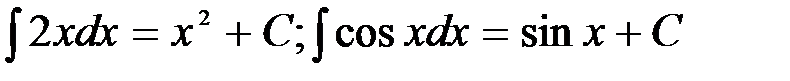 .
.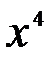 , производная которой равна
, производная которой равна  . Сделаем проверку:
. Сделаем проверку: 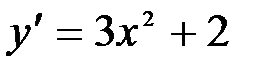 или
или  . Следовательно, интеграл найден верно.
. Следовательно, интеграл найден верно. ; отсюда следует, что
; отсюда следует, что 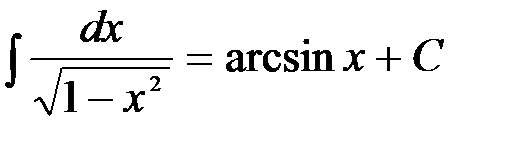 .
.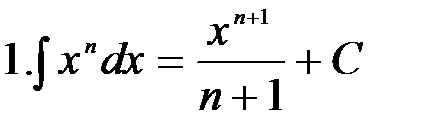 при
при 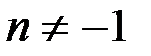
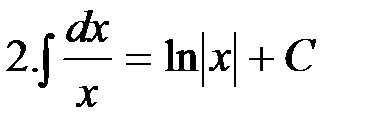
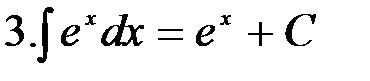
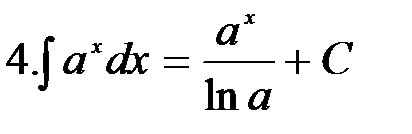
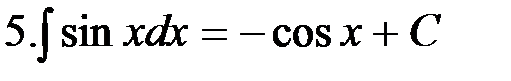
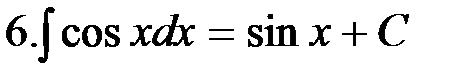
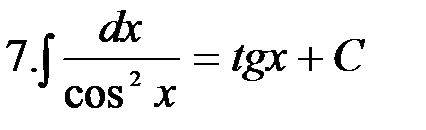
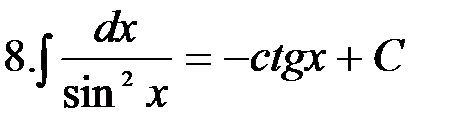
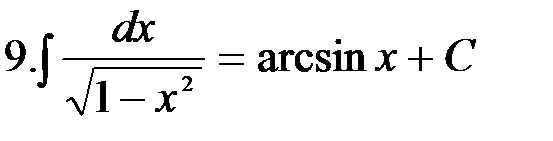
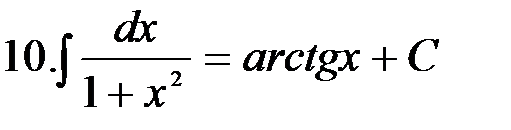
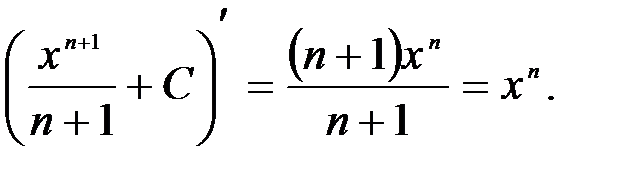
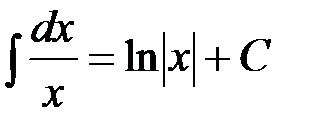
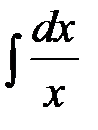 , заметим, что функция
, заметим, что функция 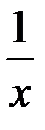 непрерывна в промежутках
непрерывна в промежутках 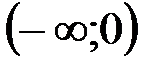 и
и 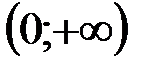 , причем в каждом из них она имеет первообразную.
, причем в каждом из них она имеет первообразную.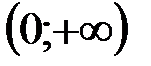 этой первообразной, очевидно, является функция
этой первообразной, очевидно, является функция 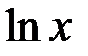 , так как
, так как 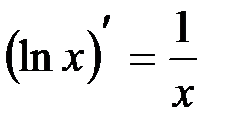 , т.е.
, т.е. 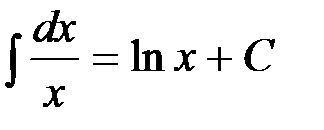 при
при 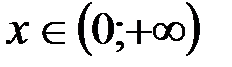 .
.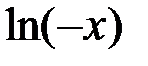 , т.е.
, т.е. 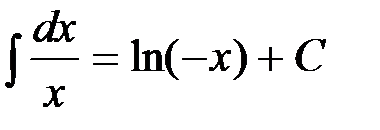 при
при 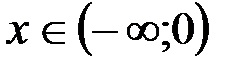 . Действительно,
. Действительно, 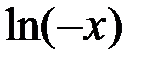 существует при
существует при  и
и 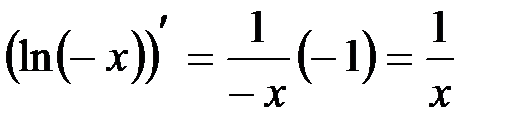 .
.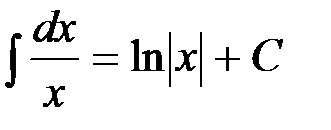 .
.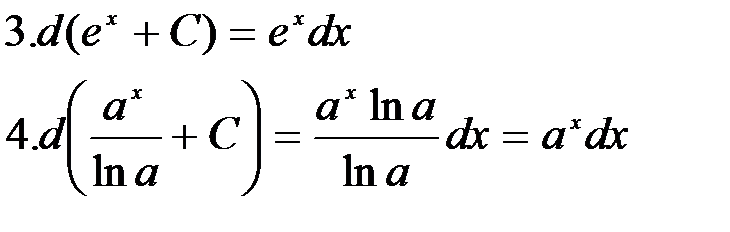
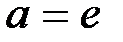 .
.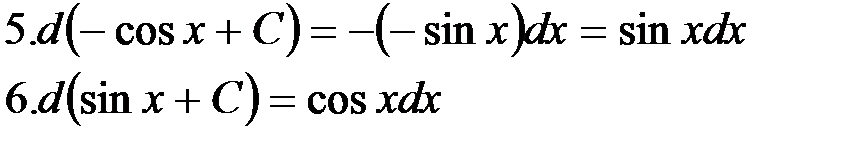
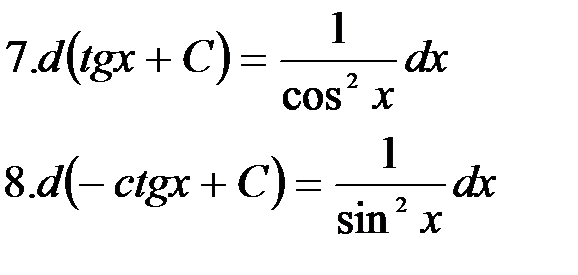
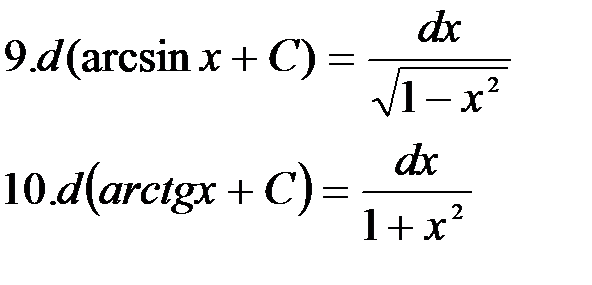
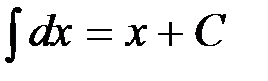 (формула 1 при
(формула 1 при 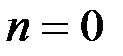 ).
).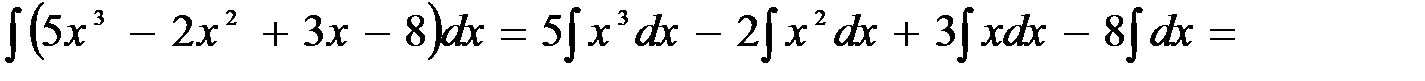
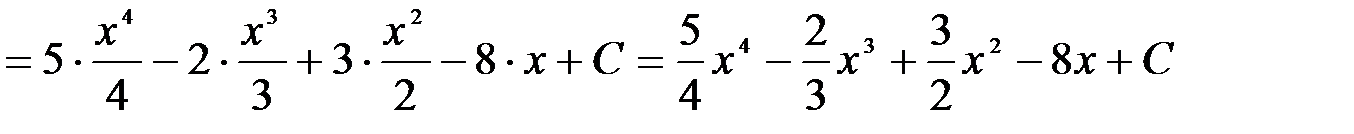
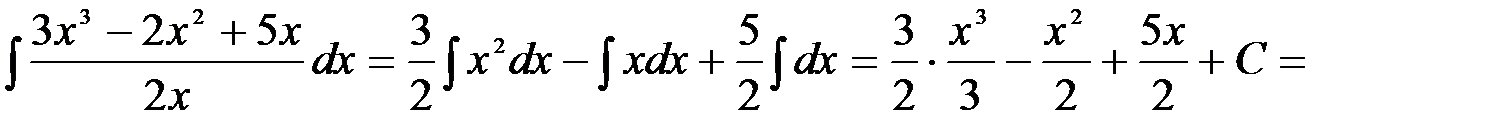
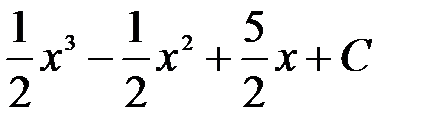
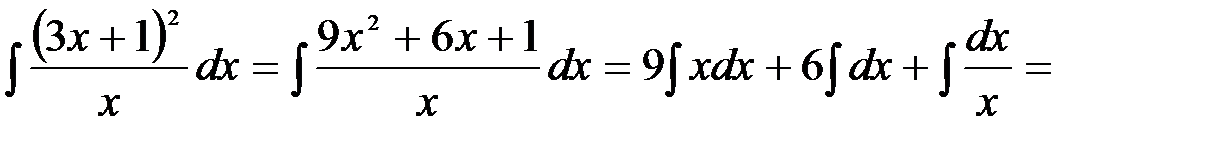
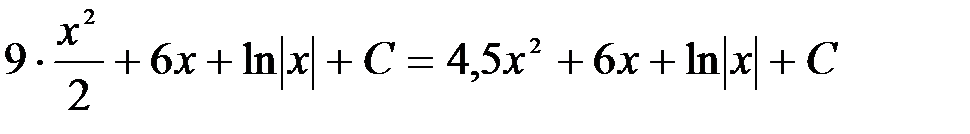
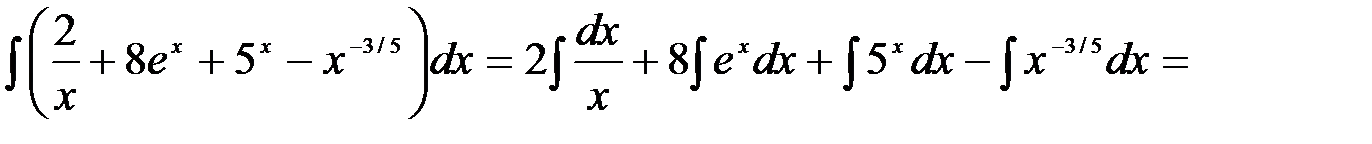
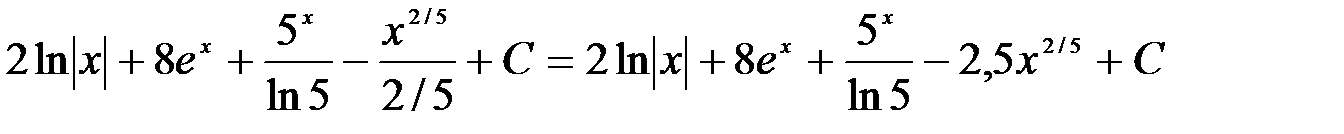
 в формуле (2) понимают простейшую из первообразных функций, у которой С=0.
в формуле (2) понимают простейшую из первообразных функций, у которой С=0. равно некоторому числу, то определенный интеграл есть число (в отличие от неопределенного интеграла, который, как известно, есть совокупность функций).
равно некоторому числу, то определенный интеграл есть число (в отличие от неопределенного интеграла, который, как известно, есть совокупность функций).  и есть площадь криволинейной трапеции, определяемой графиком функции
и есть площадь криволинейной трапеции, определяемой графиком функции  на отрезке
на отрезке  .
. (3)
(3)


