
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация моделей автоматизированного проектирования.
В автоматизированных проектных процедурах вместо ещё не существующего проектируемого объекта оперируют его моделью, которая отражает некоторые интересующие исследователя свойства объекта [3,6]. Модели могут быть физическими объектами(макет, стенд) или спецификациями (описаниями). Модели-спецификации соответствуют аспектам описания, т.е. бывают функциональные, информационные, структурные, поведенческиемодели. Эти модели называют математическими, если они реализованы средствами математического аппарата и языка математики. Этот класс моделей (математические) используется наиболее широко во всех областях техники. Как правило, если нет специальной оговорки, под термином «модель» понимают «математическую модель». Математическая функциональная модель в общем случае представляет собой алгоритм вычисления выходных параметров Y при заданных векторах входных параметров элементов X и внешних параметров Q. Модели классифицируютсяпо ряду признаков. По форме представления модели подразделяют на символические и численные. Символические модели оперируют не значениями величин, а их символическими обозначениями (идентификаторами). Численные модели в свою очередь, могут быть двух типов: · Аналитические модели, представляемые в виде выраженных зависимостей выходных параметров Y от внутренних X и внешних параметров Q; · Алгоритмические модели, в которых связь выходных параметров Y, параметров элементов X и внешних параметров Q задана неявно в виде алгоритма. Важнейшим частным случаем алгоритмических моделей являются имитационные модели, отображающие процессы в системе при наличии внешних воздействий на систему. По своей сути, имитационная модель – это алгоритмическая поведенческая модель. По характеру используемого математического аппарата моделиподразделяют натеоретико-множественные (или теоретико-эмпирические), нечёткие, абстрактно-алгебраические модели и др. Характер используемого математического аппарата во многом зависит от описываемого иерархического уровня. Например, на системном уровне преимущественно применяют модели на основе теории систем массового обслуживания, теории сетей, теории множеств и теории нечётких множеств. На функционально-логическом уровне – модели на основе аппарата передаточных функций или конечных автоматов. На макроуровне – системы алгебраических и дифференциальных уравнений. На микроуровне – алгебраические уравнения и дифференциальные уравнения в частных производных.
По степени описания внутренних процессов в объекте выделяют макромодели и полные модели. Макромодели описывают только процессы на основе изменения внешних параметров моделируемого объекта, совершенно не затрагивая внутренние процессы в объекте. Полные модели в дополнение к описанию характера изменения выходных параметров объекта, описывают также и внутренние по отношению к объекту процессы. По использованию параметра времени модели бывают статическиеи динамические. Статические модели – описывают статическое состояние объекта, время как независимая переменная не используется. Динамические модели отражают поведение системы с использованием фактора времени. В зависимости от учёта случайных факторов модели бывают стохастические (учитывающие случайные факторы) и детерминированные модели, в которых случайные факторы не учитываются. По виду фазовых переменных различают аналоговые, дискретные и смешанные модели. В аналоговых моделях фазовые переменные непрерывные величины. В дискретных моделях фазовые переменные дискретные величины. Частный случай дискретных моделей – логические (булевы) модели. В этих моделях состояние системы и её элементов описывается булевыми величинами. В смешанных моделях часть подсистем описываются аналоговыми моделями, другая часть – логическими. Наибольшие трудности возникают при создании моделей слабоструктурированных систем, характерных, прежде всего, для системного уровня проектирования. В этом случае в настоящее время достаточно широко используются модели, основанные на экспертных методах. Обычно в имитационных моделях (алгебраических, отображающих процессы в системе) фигурируют фазовые переменные. Так, на макроуровне имитационные модели представляют собой системы алгебраических и дифференциальных уравнений вида: F (dV / dt, V(t), t) = 0 (2.1)
с начальными условиями вида: при t = 0 V(0) = V 0. Здесь V – вектор фазовых переменных; t – время; V 0 – вектор начальных условий. Примерами фазовых переменных являются: скорость, координаты траектории движения объекта и др. Выходные параметры системы могут быть двух типов. Во-первых, это параметры-функционалы, т.е. функциональные зависимости V (t). Их называют характеристиками системы. Во-вторых, это параметры, характеризующие способность проектируемого объекта работать при определённых внешних условиях. Эти выходные параметры являются граничнымизначениями диапазонов внешних переменных, в которых сохраняется работоспособность объекта. Требования к математическим моделям автоматизированного проектирования. Основные требования к математическим моделям можно свести к следующим положениям: универсальность; адекватность; экономичность точность. Степень универсальности модели характеризует полноту отображения в модели свойств реального объекта. Адекватность модели – это способность отражать заданные свойства объекта с приемлемой точностью. Адекватность оценивается перечнем отражаемых свойств и областями адекватности. Область адекватности – это область в пространстве параметров, в которой погрешности модели остаются в допустимых пределах. В большинстве случаев области адекватности определяются в пространстве внешних переменных. Экономичность модели определяется затратами ресурсов, необходимых для реализации модели. Так как в САПР используются математические модели, то экономичность характеризует в данном случае вычислительную эффективность, т.е. затраты машинных ресурсов. Точность модели – это степень соответствия оценок одноименных свойств объекта и модели. Для оценки точности необходимо сравнить значения параметров объекта, рассчитанные по модели с их фактическими значениями, полученными на основании анализа статистики. Пример оценки точности математической модели [3] Рассмотрим в качестве примера оценку точности математической модели расчета относительной массы заданного элемента конструкции БЛА μ(i). Для проведения сравнительного анализа воспользуемся статистической выборкой фактических значений относительной массы рассматриваемого элемента конструкции μ(i) ф выбранных промышленных изделий. Используя требуемые для расчета по модели значения параметров выбранных изделий, определим расчетные значения относительной массы заданного элемента конструкции для каждого изделия из выборки. Относительная погрешность расчета относительной массы заданного элемента конструкции БЛА μ(i) может быть записана в виде:
где μ(i)р – расчетное (получено по модели) значение относительной массы элемента конструкции для i -го варианта БЛА из статистической выборки, включающей N вариантов; μ(i) ф – фактическое значение относительной массы данного элемента конструкции для i -го варианта БЛА из статистической выборки. После вычисления относительных погрешностей
Полученные значения математического ожидания и дисперсии относительной погрешности в определении величины относительной массы μ выбранного элемента конструкции БЛА дают некоторое представление о точности массовых формул. Однако для полноты картины необходимо определить доверительные интервалы для полученных значений точечных оценок Поскольку статистические выборки отобранных промышленных изделий, как правило, небольшие, то для оценки математического ожидания ошибки
где Для оценки дисперсии S 2, используя таблицы χ 2-распределения [7], можно найти границы доверительных интервалов этой величины, вычисляемые следующим образом:
где ε1, ε2 - табличные значения χ2 -распределения. Следует заметить, что требования по точности предъявляются не только к моделям, но и также к численным методам решения уравнений математической модели
|
|||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 118; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.37.240 (0.015 с.) |
 , (2.2)
, (2.2)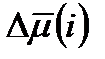 для всех вариантов БЛА можно подсчитать оценку математического ожидания (
для всех вариантов БЛА можно подсчитать оценку математического ожидания ( ) и дисперсии S 2 этих погрешностей по формулам [7]:
) и дисперсии S 2 этих погрешностей по формулам [7]: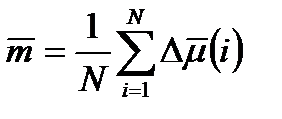 , (2.3)
, (2.3) , (2.4)
, (2.4)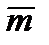 и S 2. С этой целью задаются значением доверительной вероятности p (в технике p =0,95) или уровнем значимости (α=1 - p) [7].
и S 2. С этой целью задаются значением доверительной вероятности p (в технике p =0,95) или уровнем значимости (α=1 - p) [7].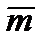 можно воспользоваться таблицами t -распределения Стьюдента. В этом случае, задаваясь величиной p (или α), находят табличное значение t -распределения Стьюдента – ε. Тогда доверительный интервал для оценки математического ожидания
можно воспользоваться таблицами t -распределения Стьюдента. В этом случае, задаваясь величиной p (или α), находят табличное значение t -распределения Стьюдента – ε. Тогда доверительный интервал для оценки математического ожидания 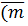 – δ) ˂
– δ) ˂  ˂ (
˂ (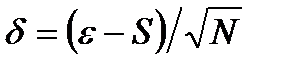 , (2.6)
, (2.6) , (2.7)
, (2.7) (2.8)
(2.8)


