
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Измерение эффективной теплопроводностиСодержание книги Поиск на нашем сайте
и температуропроводности
Эффективная температуропроводность характеризует тепловой режим псевдоожиженного слоя (например, выравнивание температур в реакторе кипящего слоя), её определение является актуальной задачей. К настоящему времени принято считать, что параметры „эффективная температуропроводность псевдоожиженного слоя“ a eff и „коэффициент диффузии“ (перемешивания) D практически тождественны: где g = 9,81 м/с2 – ускорение свободного падения, L – масштаб реактора кипящего слоя, м (обычно высота насыпного кипящего слоя Н0). Выражение (3.1) получено из известного для коэффициента турбулентной диффузии D т: где ϕ ≈ 0,1 ‒ численный коэффициент; υт – средняя скорость турбулентных пульсаций, м/с; l т ‒ масштаб пульсаций (путь смешения) турбулентного вихря, м. Физическая модель теплообмена поверхности тела, погруженного в псевдоожиженный слой представлена на рис. 3.1: а ‒ реальная, б ‒ трансформированная картина обтекания поверхности. Пакет частиц (плотная фаза) из объёма кипящего слоя подходит к поверхности теплообмена и соприкасается с ней в течение некоторого времени τ, затем уходит в объём слоя, сменяясь газовым пузырём. Эта так называемая континуальная модель внешнего теплообмена была предложена Миклеем и Фейербенксом. Частота смены газовой и плотной фаз у поверхности тела определяется частотой собственных гравитационных колебаний f 0 кипящего слоя в целом. При этом считается, что основной вклад в теплообмен вносят пакеты частиц, теплообмен с газовым пузырём пренебрежимо мал.
Рис. 3.1 – Схематическая физическая модель теплообмена тела, погружённого в псевдоожиженный слой
При прохождении пакета частиц малоинерционные преобразователи температуры, размещённые на поверхности теплообмена последовательно по вертикали, изменяют свою температуру синхронно с движением пакета. Пакет частиц границами своего контура „гонит“ температурную волну вдоль поверхности теплообмена. Вследствие этого температура поверхности θ w периодически изменяется по следующему закону:
где θ w – среднее значение температуры поверхности, около которого происходят колебания, К; Т – период колебания, с; А – коэффициент. Для псевдоожиженных систем период колебаний обратно пропорционален частоте гравитационных колебаний слоя:
Рис. 3.2 – Схема колебаний слоя а) тепловая модель для температурных волн в полупространстве; б) тепловая модель для температурных волн в стержне
Учитывая малый вклад в теплообмен газового пузыря, будем рассматривать только теплообмен поверхности с пакетом частиц. Используем тепловую модель для температурных волн в стержне (рис. 3.2, б) или полупространстве (рис. 3.2, а) в регулярном режиме третьего рода. При этом роль стержня будет играть пакет частиц с эффективными значениями тепло- и температуропроводности. Принято, что движется не пакет частиц (пакет „заморожен“), а температурная волна, которая движется вдоль оси Х, изменяя при этом амплитуду и фазу. Температура θw как функция Х и τ на расстоянии Х от О′ОО″ должна иметь вид где ϑ – амплитуда пульсаций температуры в точке с координатой Х, К. Функция ϑ должна удовлетворять, во-первых, уравнению теплопроводности Фурье: во-вторых, на поверхности О′ОО″ (т.е. при Х = 0) в любой момент времени ‒ условию: Здесь множитель Из соотношения (10) получаем уравнение для коэффициента эффективной температуропроводности пакета частиц: Расстояние обозначено Х между двумя точками l, значение τ для кипящего слоя выражается через скорость движения пакета частиц
скорость движения пакетов вычисляется по формуле: Подставив (13), (12) в (11), с учётом (4) выходит: С учётом известной формулы для частоты гравитационных колебаний: получается окончательная расчётная формула для эффективной температуропроводности пакета частиц: Эффективная температуропроводность псевдоожиженного слоя определяется объёмной долей пакетов частиц, характеризуемой порозностью слоя ε: Обычно в начале процесса псевдоожижения ε ≈ 0, 4: А в режиме развитого псевдоожижения ε ≈ 0,5-0,6: Проанализировав уравнения (3.1), (3.17), (3.19), был сделан вывод, что коэффициент температуропроводности слоя практически тождествен коэффициенту перемешивания. Формулы (3.11), (3.17) могут быть положены в основу метода измерений эффективной температуропроводности кипящего слоя: Для реализации метода достаточно иметь два малоинерционных термопреобразователя, размещённых на заданном базовом расстоянии, и преобразователь порозности (обычно ёмкостной датчик). Принципиальная схема измерений приведена в работе [6]. Конструкция первичного преобразователя является определяющей при реализации метода и должна удовлетворять следующим основным требованиям: ‒ термопреобразователи должны иметь постоянную времени не более 3-10 с и размеры, не превышающие размера пакетов частиц, но не менее десяти диаметров одиночной частицы. Для наименьшего искажения гидродинамики процесса они должны выполняться в планарном виде на изолирующей подложке с низкой теплопроводностью (керамика, металл и др.) и располагаться на массивном теле (зонде) с высокой теплопроводностью, имеющем температуру, существенно отличающуюся от температуры ядра кипящего слоя; ‒ преобразователь порозности должен быть планарного типа (оптимально-ёмкостной) и занимать ту же область, что и термопреобразователи. Апробация метода была осуществлена в лаборатории кафедры теплофизики СПбГУ ИТМО на базе устройства для измерения скорости движения частиц дисперсного потока. В результате экспериментальных исследований получены значения эффективной температуропроводности кипящего слоя из кварцевого песка с диаметром частиц 7 ⋅10 −4 м в аппарате сечением 0,2×0,2 м. Полученные значения коэффициента теплоотдачи а для разных режимов псевдоожижения находятся в пределах 0,005-0,04 м2/с. Применение тепловых методов измерения в системах с псевдоожиженным слоем представляется перспективным с точки зрения анализа не только теплофизических, но и структурно-гидродинамических параметров процессов кипящего слоя.
|
|||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 69; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.138.13 (0.008 с.) |

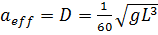 (3.1)
(3.1)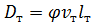 (3.2)
(3.2)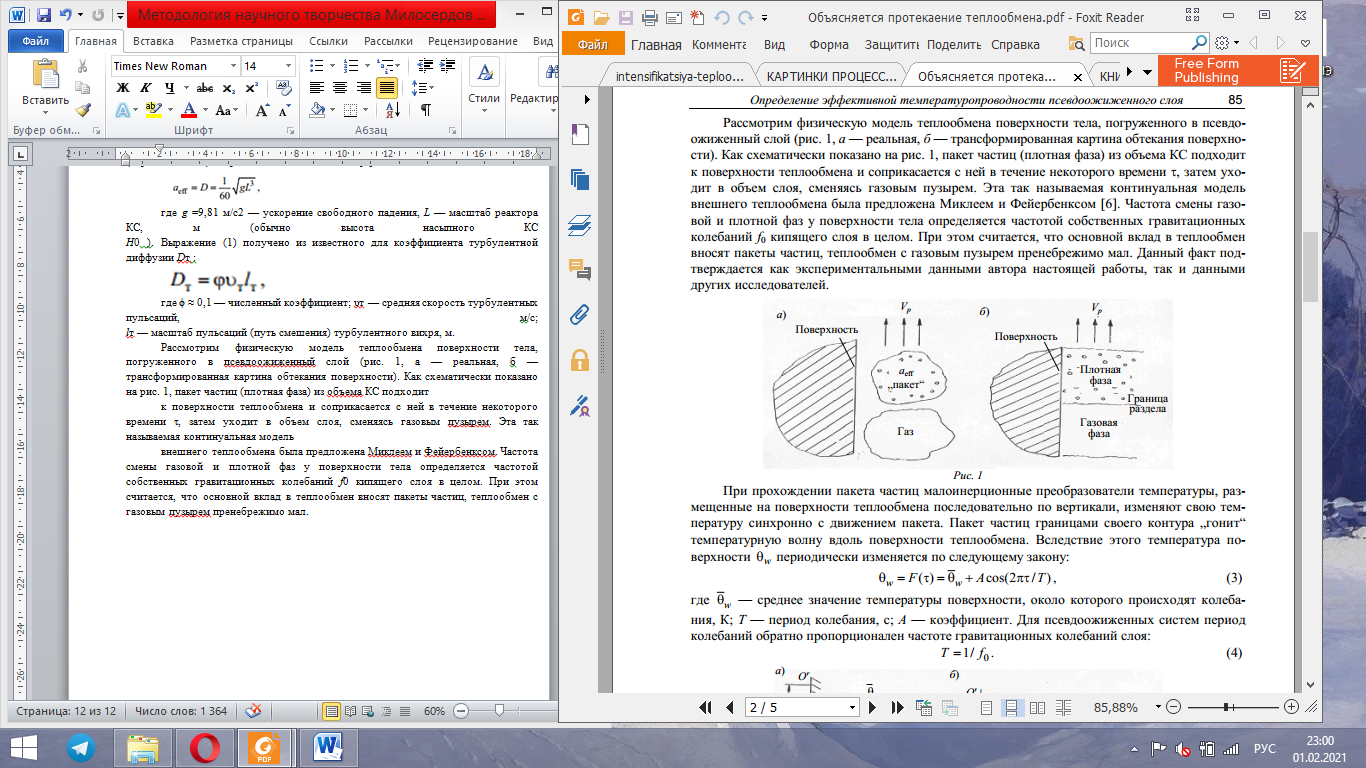
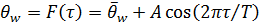 , (3.3)
, (3.3)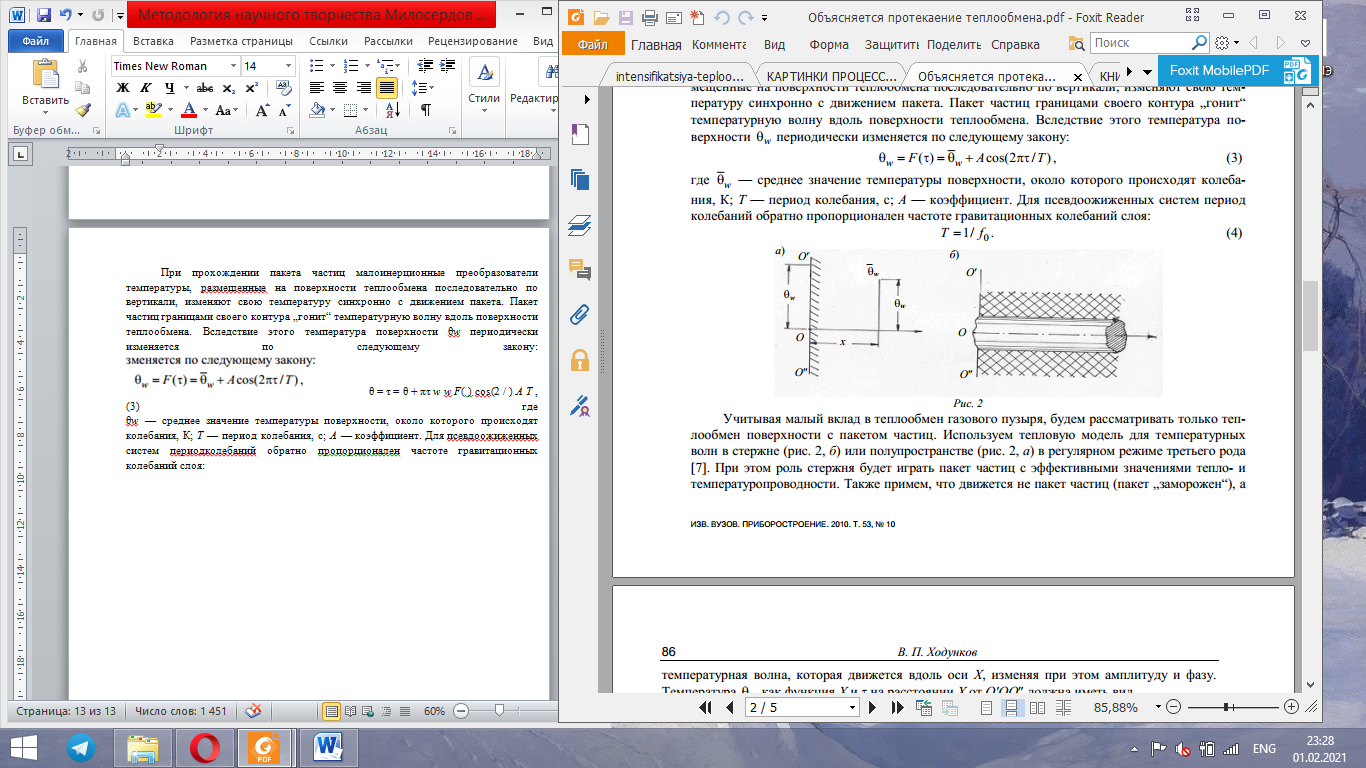
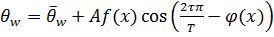 (3.5)
(3.5)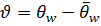 , (3.6)
, (3.6)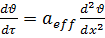 (3.7)
(3.7)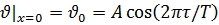 (3.8)
(3.8)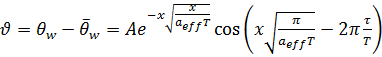 . (3.9)
. (3.9)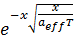 характеризует степень затухания температурной волны. В действительности для псевдоожиженного слоя такое затухание отсутствует, поэтому
характеризует степень затухания температурной волны. В действительности для псевдоожиженного слоя такое затухание отсутствует, поэтому 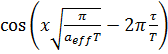 = 1. (3.10)
= 1. (3.10)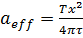 (3.11)
(3.11)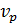 :
: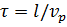 , (3.12)
, (3.12)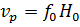 . (3.13)
. (3.13)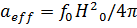 . (3.14)
. (3.14)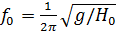 (3.15)
(3.15)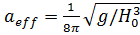 . (3.16)
. (3.16)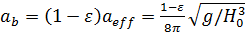 (3.17)
(3.17)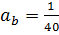
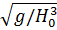 , (3.18)
, (3.18)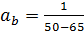
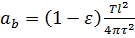 (3.20)
(3.20)


