Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основы теории оболочек вращенияСтр 1 из 6Следующая ⇒
Краевой эффект. В случае осесимметричной деформации положим Полная система уравнений будет иметь вид:
Если нагрузки Рассмотрим однородные уравнения, когда
где Будем также считать, что величина Положим, что
Из этих уравнений следует, что
Из соотношения (51) с той же точностью следует
Уравнения равновесия (52) и (53) сразу упростить нельзя, так как неизвестен относительный порядок величин
Умножив последнее уравнение на
Константа соответствующая продольной силе
Уравнение для краевого эффекта примет вид
Сравним порядки величин меридионального и окружного усилий в краевой зоне.
Следовательно получим
Подставив эту зависимость в выражение (59), получим
Обозначим
Для сферической оболочки При k=const получаем
Где A,B,C и D - произвольные константы. Выражение (61) обладает тем свойством, что при каждом дифференцировании оно возрастает в k раз:
Следовательно, это решение удовлетворяет условию малости функции по сравнению с производной. Рассмотрим затухающую часть выражения (61):
Величины
Рассмотрим последовательность расчета осесимметрично нагруженной оболочки вращения по моментной теории с разделением напряженного состояния на безмоментное и краевой эффект. Сначала по безмоментной теории определяют силы Тъ Т2 и перемещения и, w по заданным внешним нагрузкам и граничным условиям для величины Тх или и. (В выражение для перемещений может входить константа интегрирования, соответствующая перемещению оболочки как твердого тела.) Затем, решая однородные уравнения краевого эффекта для каждого торца, находят общие выражения для величин е2, ЪХУ Мг и Qx через соответствующие константы интегрирования (по две константы на каждом торце). Наконец, составляют граничные условия для каждого торца оболочки. Если заданы силовые граничные условия, т. е. величины Мг и Ql9 то сразу определяют константы интегрирования уравнений краевого эффекта. Если заданы геометрические условия, т. е. величины s2 и то по значениям перемещений и и w безмоментного решения определяют величины е2о и OlQ (перемещение оболочки как твердого тела в них не войдет) и составляют суммарные выражения для е2 и $г от безмоментного решения и краевого эффекта. Константы интегрирования, входящие в эти выражения, определяют из заданных геометрических граничных условий.
Расчёт баков Исходными данными для расчетов на прочность баков являются внешние нагрузки и температурное состояние конструкции.
В поперечном сечении бака действуют изгибающий момент М, осевая сжимающая сила N и перерезывающая сила Q. От внутреннего давления Р = р0 + пхуН, (11.1) момента М и сил N и Q в обечайке бака возникают меридиональные T 1, окружные Т2 и сдвигающие S погонные силы. Их наибольшие значения равны T 1 =[ N /(2 πR)± M /(πR 2)- poR /2]; (11.2) T2 = (po+nxγH)R; (11.3) S = Q/(πR). (11.4) Положительные значения сил T 1 и Т2 соответствуют растягивающим напряжениям. Сдвигающая сила S в расчетах на прочность баков является менее важным фактором. Значения сил При малых значениях давления наддува меридиональная сила T 1, возникающая в обечайке корпуса бака, оказывается сжимающей. Сжатая в осевом направлении обечайка может потерять устойчивость. Напряжения, при которых происходит потеря устойчивости обечайки Гладкого бака, весьма невелики. Для повышения устойчивости обе чайки можно применить панели стрингерной или вафельной конструкции. Другой путь — увеличение давления наддува р0 в баке. Большие давления р0 приводят к растяжению обечайки вдоль образующей. При этом окружные силы T 2 по формуле (11.3) оказываются большими. При больших окружных растягивающих усилиях баки целесообразно выполнять из высокопрочных материалов. Отсутствие осевого сжатия позволяет делать обечайки неподкрепленными. Давление наддува в них обычно выбирают так, чтобы в осевом направлении не возникали сжимающие напряжения от силы N и момента М:
(poR)/2≥|N/(2πR)|+|M/(πR2)|
Суммарные осевые напряжения при этом сравнительно невелики. Однако внутреннее давление создает большие окружные напряжения σ2 = (po+nxγH) Возможны два вида напряженного состояния обечайки бака: 1) окружная Т2 и меридиональная 7\ силы — растягивающие (этот случай характерен для такого нагружения баков, когда абсолютные значения первых двух слагаемых правой части формулы (11.2) меньше третьего слагаемого); 2) окружная сила Т2 растягивающая, а меридиональная сила Тг — сжимающая. В обоих случаях меридиональная сила, как правило, по модулю существенно меньше окружной. При Т2 > 0 и T1 > 0 расчет баков на прочность ведут только от окружных усилий. В проектировочном расчете из условия прочности обечайки в окружном направлении определяют ее толщину, в проверочном - при известной толщине определяют расчетные напряжения σр. Эти напряжения должны быть меньше предела прочности материала
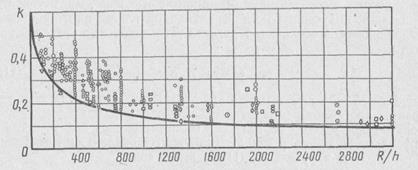
σр=(T2/h)f≤σВ (11.5) Если баки сжаты в осевом направлении (Т2 > 0; T1 < 0), то для каждой комбинации сил Т2 и Т1 в различных сечениях определяют эквивалентные напряжения: σэ = (Т2 – T 1)/ h, (11.6) а расчетные напряжения находят по формуле ар = f стэ. С учетом знака суммарные напряжения здесь будут больше, чем соответствующие окружные. Полученные напряжения при этом должны удовлетворять условию прочности σр≤σВ. Обечайку бака рассматривают как изотропную оболочку, нагруженную сжимающей силой, изгибающим моментом и внутренним давлением. Напряжения, соответствующие потере устойчивости такой оболочки, σхл = (kхлEh)/R, (11.7) где Е — модуль упругости материала оболочки; h — толщина оболочки; R —ее радиус; kхл — коэффициент устойчивости. В практических расчетах коэффициент σхл можно представить в форме σхл= k ∙ kp ∙ kM ∙ ki (11.8) Каждый из коэффициентов в этой формуле отражает влияние определенного фактора: k — влияние начальных несовершенств оболочки; kp — влияние внутреннего давления; kM — неравномерность распределения сжимающих напряжений по сечению, возникающих от осевого сжатия и изгиба; ki — влияние пластических деформаций. Рассмотрим вкратце влияние каждого фактора в отдельности на устойчивость оболочки. Влияние начальных несовершенств. Напряжения, соответствующие потере устойчивости оболочки, существенно зависят от начальных несовершенств (начальных неправильностей формы): чем больше отклонения от идеальной формы, тем ниже критическое напряжение. Практически влияние начальных несовершенств возрастает с уменьшением относительной толщины оболочки h / R. Поэтому коэффициент, учитывающий влияние Начальных Несовершенств, можно представить как функцию k = k (h / R). Для тщательно изготовленных обечаек баков можно принять k =0.605-0.545[1-exp(-1/16∙√(R/h))¯] (11.9) Так, например, для оболочки, имеющей параметр h / R = 1/500, k =0,2 при h / R = 1/1800, k = 0,1. На рис. 11.4 изображена зависимость (11.9) и результаты ряда экспериментов [17].
Влияние внутреннего давления.
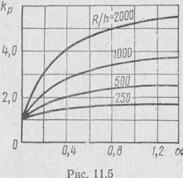
Теоретические и экспериментальные исследования показывают, что внутреннее давление существенно влияет на устойчивость цилиндрической оболочки, нагруженной осевыми силами. Зависимость коэффициента устойчивости от внутреннего давления может быть отражена соотношением Kp=[1+0.21α(R/h)0.6]/(1+3α) (11.10) где α=(pR2)/(Eh2) На рис. 11.5 представлены кривые kp (α) для разных отношений R / h. Существенное увеличение коэффициента устойчивости особенно характерно для очень тонких оболочек. Влияние неравномерности распределения сжимающих напряжений. Сравнение коэффициентов устойчивости для цилиндрической оболочки, нагруженной осевой силой и нагруженной изгибающим моментом, показывает, что при одинаковых сжимающих напряжениях устойчивость оболочки при изгибе примерно на 25 % выше, чем при осевом сжатии. Совместное действие изгибающего момента и осевой силы можно учесть коэффициентом kM=(1+1.25∙2M/(NR))/(1+2M/(NR))
где N и М — соответственно осевая сила с учетом разгрузки от давления и изгибающий момент в сечении; R — радиус обечайки. Влияние пластических деформаций. Потеря устойчивости большинства сжатых и нагруженных внутренним давлением тонкостенных гладких оболочек происходит в упругой области при сравнительно низком уровне сжимающих напряжений. Однако в некоторых случаях, при определенном соотношении осевых и окружных напряжений, в оболочке могут возникать пластические деформации. Напряжение потери устойчивости оболочки при этом снизится. Потеря устойчивости будет происходить с образованием осесимметричных волн. Критические напряжения, полученные по деформационной теории пластичности для цилиндрической оболочки, теряющей устойчивость за пределом упругости, σ1кр=2/3∙√ЕкЕс¯(h/R) (11.12) где Ек и Ес — соответственно касательный и секущий модули диаграммы растяжения материала обблочки; числовой коэффициент 2/3 получен при условии образования осесимметричной волны, когда коэффициент Пуассона μ = 0,5. Для упругой области деформирования Eк = Ес = Еи уравнение (11.12) имеет вид σкр=2/3∙E(h/R) Коэффициент, показывающий, во сколько раз напряжения потери устойчивости в пластической области меньше, чем в упругой, при одной и той же деформации, равен ki =√ EkEc ¯/ E (11.13) Для оболочки, находящейся в двухосном напряженном состоянии, значение коэффициента ki можно найти после определения интенсивности напряжений σi =√ σ 1 2 - σ 1 σ 2 + σ 2 2 ¯ (11.14) Предварительно рассмотрим, как определить коэффициент ki при заданных значениях σ1 и σ2. По известной диаграмме растяжения σi-εi материала оболочки можно построить зависимости Ек(ε) и Ес(ε). Для известных напряжений σ1 и σ2 по уравнению (11.14) находим значение σ i и затем εi, по которому определяем модули Ек и Ес, и из уравнения (11.13) вычисляем коэффициент ki. Необходимо иметь в виду, что при осевом сжатии члены под корнем в выражении (11.14) суммируются и σхл = -σ1
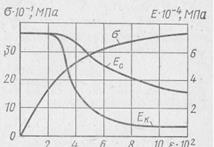
На рис. 11.6 построена диаграмма растяжения алюминиевого сплава. Здесь же приведены зависимости Ек(ε) и Ec(ε). Из этих кривых и соотношений (11.13) и (11.14) видно, что растяжение в окружном направлении сжатой по оси цилиндрической оболочки вызывает уменьшение критических напряжений в том случае, когда интенсивность напряжений в оболочке выше предела упругости. Итак, учитывая основные факторы, влияющие на устойчивости цилиндрической обечайки бака, с помощью уравнений (11.9), (11.10), (11.11) и (11.13) можно получить значение коэффициента устойчивости kхл. Однако критические напряжения по коэффициенту устойчивости найти сразу не удается, если в оболочке возникают пластические деформации. Обратим внимание на то, что значение самого коэффициента kхл зависит от уровня напряжений. Чтобы определить напряжения, соответствующие потере устойчивости оболочки, можно воспользоваться методом последовательных приближений. В первом приближении можно брать коэффициент k = 1, т. е. считать, что оболочка работает в упругой области. Затем по зависимостям (11.7) и (11.8) можно определить критические напряжения σхл = -σ1. Далее при известном давлении находят σ2 = (pR)/ h и по уравнению (11.14)—интенсивность напряжений σi;. По рис. 11.6 определяют модули Ек и Ес, а по уравнению (11.13) — новый коэффициент ki. Умножив его на величину k kpkM, получают значение коэффициента kхл второго приближения. Далее находят критические напряжения второго приближения и т. д. Иногда в качестве первого приближения лучше взять ki = 0,6... 0,8. В ряде случаев это существенно ускоряет расчет. Отметим, что теоретической верхней границей коэффициента устойчивости kхл является величина 0,605. Однако практически не удается получить kхл > 0,45. Изложенный метод расчета позволяет приближенно установить зависимости критических напряжений хлопка от различных факторов. Для уточнения расчетов нужно пользоваться результатами экспериментов с баками или их моделями.
Пример. Обечайка бака гладкой конструкции толщиной h = 3 мм и радиусом R = 1500 мм из алюминиевого сплава (Е = 72 000 МПа) нагружена осевой силой N и изгибающим моментом М, причем 2 M /(NR) = 0,2. Требуется определить напряжения, соответствующие потере устойчивости оболочки при р = 0. Из соотношений (11.9), (11.10), (11.11) для R / h = 500 определяем коэффициенты k = 0,2; kp = 1; kM = 1,04 и берем ft. = 1. Коэффициент ftxjl = kkpkMkt = 0,2-1-1,04-1 = 0,208. Критическое напряжение хлопка согласно формуле (11.7) о-хл = k ^ EhlR = (0,208-7,2.10V500) МПа = 30 МПа. Далее находим критические напряжения хлопка обечайки бака под давлением р и строим зависимость 0ХЛ = / (р). (Диаграмма растяжения материала бака изображена на рис. 11.6.) По зависимостям (11.9)... (11.11) для h / R = 1/500 при различных давлениях р = 0,1; 0,2; 0,3; 0,4; 0,5 МПа определяем коэффициенты ftp, kM, ftr Затем определяем ст2 = pR / h. По зависимости (11.7) находим напряжение ахл, полагая вначале ftj = 1. Затем проверяем, чему равен коэф-
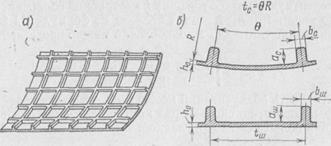
Баки вафельной конструкции Расчет обечайки бака вафельной конструкции (рис. 11.8, а) состоит в определении напряжений, соответствующих потере устойчивости при действии осевых сил и внутреннего давления. Кроме того, необходимо выполнить расчет на прочность различных сечений обечайки. Расчет на устойчивость. Для проведения расчета на устойчивость и определения напряженного состояния воспользуемся схемой конструктивно-анизотропной оболочки. При расчете по этой схеме считается, что оболочка при растяжении и изгибе в продольном и поперечном напрявлениях имеет один и тот же модуль упругости, но разную толщину. На рис. 11.8, б изображены элементы сечений оболочки. Площади сечений поперечных и продольных подкрепляющих элементов обозначим через Sш = b ш a ш и Sc = bcac (11.16) Здесь и далее индекс «ш» соответствует поперечным подкреплениям (шпангоутам), а «с» — продольным (стрингерам). Приведенные т олщины оболочки при растяжении в кольцевом и меридиональном направлениях будут соответственно hш = h 0 + Sm / t ш, hc = h 0 + Sc / t с, (11.17) где h 0 — толщина обшивки; te и t ш — шаг подкреплений. Подсчитав момент инерции элементов относительно центр а тяжести сечений, можно найти приведенные толщины при изгибе δш=3√12Jш/tш¯; δс=3√12Jс/tс ¯ (11.18) При подсчете момента инерции Jc обычно пренебрегают кривизной оболочки. Эквивалентную толщину h гладкой оболочки, равной по массе оболочке вафельной конструкции, определяют из равенства htctш = hоtctш+ Sct ш + Smtc + S ш t с, (11.19) откуда h = h ш + h с - h0. (11.20) Для гладкой оболочки площади подкреплений равны нулю (Sш = Sс = 0) и толщины h ш = =h0= δш = δс=ho. Для вафельной конструкции справедливы соотношения δш/δc≈hш/hc≈1. Однако величины δш и δс, как правило, в несколько раз больше, чем hш и hc: δш/hш»1 и δc/hc» 1. (11.21) Иначе говоря подкрепления в большей степени увеличивают изгибную жесткость, чем жесткость на растяжение. Будем считать, что деформация и форма потери устойчивости оболочки под действием внешних нагрузок осесимметричны. В § 8.2 приведены уравнения устойчивости цилиндрической оболочки. Учитывая обозначения (11.17), (11.18) и полагая коэффициент
Пуассона мало влияющим на деформацию оболочки и поэтому равным нулю, уравнение устойчивости конструктивно-анизотропной оболочки примет вид E (δc 3 /12)(d 4 ω / dx 4)+ T 1 (d 2 ω / dx 2)+(Eh ш/ R 2) ω =0 (11.22)
Уравнение для изотропной оболочки имеет такую же форму, но коэффициенты. E (δc 3 /12) и Eh ш/ R 2 заменяют величинами D и Eh / R 2, соответствующими жесткости на изгиб и растяжение изотропной оболочки. При потере устойчивости с формой волнообразования ω = sinλ х, где λ — параметр длины волны, из последнего уравнения можно получить выражение для осевой силы T1= E (δc 3 /12) λ 2 +(Eh ш/ R 2)∙1/ λ 2 Определим критическую силу при осесимметричной форме потери устойчивости оболочки, приравняв нулю производную от T1 по λ2, T кр = E / R √ δc 3 h ш /3¯. (11.23) При этом λ =4√12 h ш (R 2 δc 3)¯ и длина полуволны оболочки l = π /λ, т. е. l=π 4 √ R 2 δc 3 /(12 h ш)¯. Критическая осевая сила равна Nкр=(2π/√3¯)E√ δc 3 h ш ¯ (11.24) Для изотропной оболочки эквивалентной толщины h при тех же условиях критическая сила равна T1кр=√1/3¯(E/R)h2 (11.25) Эквивалентную по массе толщину h изотропной оболочки, выраженную через параметры h 0, h ш и hc, находят по формуле (11.20). Значение критической силы для этой оболочки можно представить в виде T1кр= √1/3¯(E/R) (h ш + hu - h 0)2 (11.26) Эффективность подкреплений может быть отражена коэффициентом feBl, показывающим, во сколько раз критическая сила для вафельной конструкции больше силы для гладкой: Kв1=√ δc 3 h ш ¯/(h ш + hu - h 0)2 (11.27) У вафельной оболочки толщины hu и h ш близки по значению друг другу: h ш ≈ h с ≈ (1,2... 1,5) h 0. Изгибная толщина лежит в пределах δс = (2,0... 5,0) h 0. При этом коэффциент kв1= 2... 3. Чтобы оценить, во сколько раз критические напряжения подкрепленной конструкции больше, чем гладкой, нужно соотношения (11.23) и (11.25), отнесенные соответственно к hc и h, поделить друг на друга: kв=1/ (h ш + hu - h 0) √ δc 3 h ш / h с 2 ¯ (11.28) Расчетное критическое напряжение для вафельной обечайки бака можно представить в форме σхл=kв∙хлEh/R (11.29) где h - эквивалентная толщина оболочки, определяемая соотношением (11.20): kв∙хл=kkpkмkikв Коэффициенты k,kp,kм,kiотражают соответственно влияние начальных несовершенств оболочки, внутреннего давления, изгибающего момента и пластических деформаций. Значения этих коэффициентов и зависимость их от соответствующих факторов представлены в § 11.2. Коэффициент kв устанавливает зависимость напряжения σхл от конструктивных особенностей оболочки и определяется по формуле (11.28). Значение коэффициента kв∙хл здесь может существенно превосходить величину 0,605. При определении осевых напряжений в оболочке бака предполагалось, что на сжатие все сечение работает равномерно. Это возможно лишь при отсутствии местных вмятин панелей в ячейках. В окончательных расчетах следует определять значения местных критических напряжений панели. Напряжения, соответствующие местной потере устойчивости панели между ребрами, определяют по уравнению σкр= k хл Eho / R + k п E (ho / tc)2 (11.31)
Коэффициент kхл определяется уравнением (11.8). Для вычисления приближенного значения коэффициента kхл можно учитывать лишь коэффициенты k и kp, определяемые по формулам (11.9) и (11.10). Для заделанной по краям квадратной панели (tc = tш) коэффициент kn = 8,4. При отношении t ш / t с ≠ 1 можно использовать коэффициент для kn сжатой в одном направлении плоской пластины, заделанной со всех сторон. Сжатые продольные ребра проверяют на устойчивость. Для прямоугольных ребер критические напряжения потери местной устойчивости σкр = 0,9 ∙ 0,46 Е (bс/ас)2. (11.32) Расчет на прочность. Окружные напряжения для безмоментной Конструктивно-анизотропной оболочки определяются соотношением σ2 = рR/hш. (11.33) Меридиональные напряжения в обечайке бака σ1 = T1/hc. (11.34) Это выражение справедливо до момента образования вмятин в ячейках, т. е. до потери местной устойчивости. Расчет на прочность обечайки бака состоит в определении напряжений σ2 и σ1 для ряда сечений. По известным окружным и меридиональным напряжениям находят эквивалентные напряжения. Для этого можно воспользоваться условиями σэ = σ2-σ1 . (11.35) или σэ=√σ12-σ1σ2+σ22¯. (11.36) При расчете на прочность баков обычно пользуются уравнением (11.35), из которого находят расчетные напряжения σp=f(σ2-σ1), (11.37). где f-коэффициент безопасности. Это уравнение и зависимости (11.33) и (11.34) позволяют в проектировочных расчетах найти приведенную толщину оболочки, если принять hc ≈ h ш.
Пример. Обрлочка вафельной конструкции из алюминиевого сплава Е = = 72 000 МПа, имеющая предел упругости Сту = 250 МПа, нагружена осевым сжатием и внутренним давлением р =' 0,3 МПа. Параметры оболочки: радиус R = 1500 мм, шаг подкреплений /ш = fc = t = 1200 мм, толщина обшивки Ад = 2,0 мм, высота ребер аш — ас = а = 10 мм, ширина ребер 6Ш = Ьс = = 6=6 мм. Требуется определить расчетные напряжения хлопка оболочки и значение окружного напряжения. Приведенная толщина оболочки согласно формуле (11.17) Площадь подкреплений. Для определения момента инерции нужно найти центр тяжести сечения. Относительно наружной поверхности оболочки координата центра тяжести. Момент инерции сечения. Приведенные толщины на изгиб по формуле (11.18). Эквивалентную по массе толщину оболочки находим по формуле (11.20); Для оболочки гладкой конструкции с толщиной А = 3 мм в предыдущем параграфе "было определено расчетное напряжение стхл = 30 МПа при давлении р = 0; при этом коэффициент fexn = 0,208. Чтобы определить коэффициент устойчивости kB. хл Для вафельной оболочки, нужно коэффициент £хл = 0,208 умножить на значение kB, найденное по формуле (11.28): VW * Уб,12з.2,5 (Лш + Л0-Ло)Ав (2,5 + 2,5-2)2,5 = откуда /гв.хл=-=£хл£в = 0,208-3,16 = 0,657. Расчетные напряжения потери устойчивости вафельной обечайки бака об.зл = kf.^ Eh / R = (0,657-7,2-10V500) МПа = 94,5 МПа, или в 3,16 раза больше напряжений гладкой оболочки той же массы. Для эквивалентной по массе гладкой обечайки бака, находящейся под давлением р = 0,3 МПа, коэффициент йхл = 0,517 (см. § 11.2), Тогда расчетные напряжения потери устойчивости для вафельной обечайки будут Ов.хд= kKuksEh / R = (0,517-3,16-7,2.10*7500) МПа = 235 МПа. Окружные напряжения в обечайке бака при р = 0,3 МПа определим по зависимости (11.33): а3= pR / hm = (0,3-1500/2,5) МПа = 180 МПа. > Схема конструктивно-анизотропной оболочки при расчете напряжений в вафельной обечайке бака является приближенной. Для построения уточненных полей напряжений в вафельных ячейках необходимо пользоваться такими более совершенными методами расчета, как МКР или МКЭ. Расчет днищ баков При расчете на прочность днища рассматриваются как безмомент-ные оболочки вращения, нагруженные осесимметричной нагрузкой. Напряжения от изгиба в местах соединения днища бака е обечайкой и в зоне крепления фланцев, как правило, в расчет не принимаются. Изготовляют днища обычно из пластических материалов, для которых местный изгиб не является причиной разрушения. В зоне фланцевых соединений люков и трубопроводов происходит перераспределение мембранных напряжений. Расчеты показывают, что фланцы влияют на напряженное состояние лишь локально. Не учитывают также составляющие нагрузки от массы конструкции бака. При расчете днищ прежде всего необходимо определить внутренние погонные меридиональные T1 и окружные Т2 силы. Определение внутренних сил. Напряженное состояние безмомент-ной оболочки вращения, нагруженной нормальным давлением рп (рө= 0), описывается уравнениями: (1/R1)(dT1/dӨ)+(T1-T2)cosӨ/r=0 (11.38)
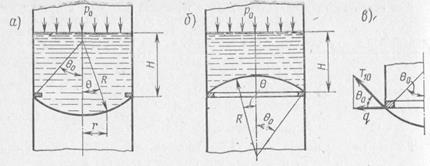
T1/R1+T2/R2=pn (11.39) С помощью этих уравнений найдем окружные и меридиональные силы в днищах различной конфигурации. 1. У сферического днища (рис. 11.9, а) давление на поверхности днища pn = p = p 0 + nxγ [ H + R (cos Ө - cos Ө0)]. (11.40) Воспользовавшись очевидными соотношениями для сферы r = Rsin Ө, dr = Rcos Ө d Ө, R 1 = R 2 = R, после интегрирования уравнения (11.38), учитывая соотношения (11.39) и (11.40), получим T1 = [ p 0 + nxγ (H-RcosӨ0)]R/2- nxγ R2(cos3Ө/3sin2Ө)+C. Постоянная С определяется из условия конечного значения силы T1 в полюсе оболочки при Ө=0. Тогда выражение для меридиональной силы в сферическом днище будет следующим: T1=p0R/2+nxγHR/2[1+R/H(2/3∙ (1-cos3Ө/sin2Ө)-cosӨ0)] (11.41)
Окружная сила находится из уравнения (11.39) Т2 = p0R/2+ nxγHR/2 [1+R/H(2cosӨ-cosӨ0-2/3∙ (1-cos3Ө/sin2Ө))] (11.42)
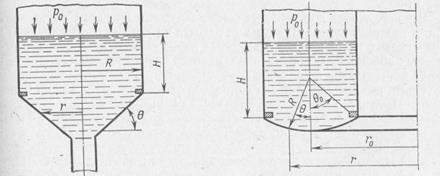
Окружные и меридиональные силы имеют максимальные значения в полюсе при Ө= 0; при этом член в круглых скобках выражения (11.41) стремится к единице: T1max=T2max= p0R/2+ nxγHR/2[1+R/H(1-cosӨ0)] (11.43) В месте сопряжения днища с кольцом при Ө=Ө0 меридиональная сила T1o= p0R/2+ nxγHR/2[1+R/H(2/3∙ (1-cos3Ө/sin2Ө)-cosӨ0] (11.44) а радиальная составляющая, сжимающая кольцо в его плоскости (рис. 11.9, в), q= Т1o cos Ө0. (11.45) В сферическом днище, изображенном на рис. 11.9, б, силы T1 и Т2 определяют в той же последовательности, что и в предыдущем случае: T1= - p0R/2- nxγHR/2[1-R/H(2/3∙ (1-cos3Ө/sin2Ө)-cosӨ0] (11.46) T2= - p0R/2- nxγHR/2[1-R/H(2cosӨ-cosӨ0 - 2/3∙ (1-cos3Ө/sin2Ө)] (11.47) Если днище выполняет роль перегородки между двумя баками, во всех соотношениях давление наддува р0 следует заменить перепадом давлений Δp. 2. У конического днища (рис. 11.10) давление на оболочку распределено по закону P = Po + nx γ H (1+(R - r)/ H ∙ tg Ө]. (11.48)
Из уравнений (11.38) и (11.39) определяют меридиональную и окружную силу: T1=p0r/(2sinӨ) + (nx γ H /( 2sinӨ ))∙ r [1+ (R/H-2/3∙ r/H)tgӨ ] (11.49) T2=p0r/(sinӨ) + (nx γ H /( sinӨ ))∙ r [1+ (R/H- r/H)tgӨ ] (11.50) Сила, приложенная к кольцу крепления днища, определяется соотношениями, (11.45) и (11.49), куда вместо угла 8 нужно подставить Ө0. 3. У торообразного днища различают меридиональный R 1 = R и окружной R2=R+r0/sin Ө радиусы кривизны. Закон распределения давления по углу Ө определяется соотношением (11.40).
Интегрируя уравнение (11.38) и используя условие ограниченности силы при Ө = 0, получаем выражение для меридиональной силы:
T1=p0R[(ro+(R/2)sinӨ)/(ro+RsinӨ)]+[(nxγHR2)/(ro+RsinӨ)] ∙ [r0/R(1-((R/H))cosӨ0)+
+(r0/2H)∙Ө/sinӨ+r0cosӨ/2H+(1/2)sinӨ(1-(R/H)cosӨ0)+ (R/3H)/((1-cos3Ө)/sin2Ө)] (11.51)
Окружную силу находят из уравнения (11.39):
T2=p0R/2+ nxγHR∙1/2[(1-((R/H))cosӨ0) +(r0/H)∙(Ө/sin2Ө)∙(sinӨcosӨ-Ө)+
+(2R/H)cosӨ-(2R/3H)(1-cos3Ө)/sin2Ө)] (11.52) Основы теории оболочек вращения Оболочка - тонкостенная конструкция, с постоянной толщиной.
Основным геометрически понятием теории оболочек постоянной толщины являются понятия срединной поверхности и слоя оболочк
|
|||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 362; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.55.14 (0.221 с.) |
 и все величины - не зависящими от угловой координаты
и все величины - не зависящими от угловой координаты 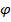 . В этом случае
. В этом случае 
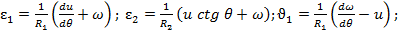 (47)
(47)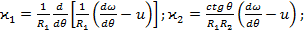 (48)
(48)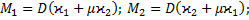 (49)
(49)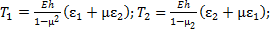 (50)
(50)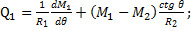 (51)
(51)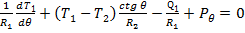 (52)
(52) (53)
(53)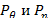 меняются вдоль меридиана достаточно плавно, частное решение уравнений можно, как уже указывалось, найти по формулам безмоментной теории оболочек.
меняются вдоль меридиана достаточно плавно, частное решение уравнений можно, как уже указывалось, найти по формулам безмоментной теории оболочек.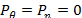 . Моментное напряженное состояние при осесимметричной деформации теряет смысл, так как из решения уравнений
. Моментное напряженное состояние при осесимметричной деформации теряет смысл, так как из решения уравнений  получаются перемещения и и w, соответствующие лишь движению оболочки как твердого тела вдоль оси симметрии. Для приближенного определения смешанного напряженного состояния, которое соответствует краевому эффекту, рассмотрим упрощения исходных уравнений, следующие из условия быстрой изменяемости напряженного состояния вдоль меридиана. Будем считать,-что для всех искомых сил и перемещений выполняется условие
получаются перемещения и и w, соответствующие лишь движению оболочки как твердого тела вдоль оси симметрии. Для приближенного определения смешанного напряженного состояния, которое соответствует краевому эффекту, рассмотрим упрощения исходных уравнений, следующие из условия быстрой изменяемости напряженного состояния вдоль меридиана. Будем считать,-что для всех искомых сил и перемещений выполняется условие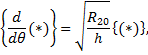
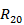 — окружной радиус кривизны у края оболочки.
— окружной радиус кривизны у края оболочки.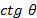 для любого края оболочки не слишком велика и радиусы кривизны Rl, R2 изменяются вдоль меридиана достаточно плавно. Естественно предположить, что порядок величины перемещения
для любого края оболочки не слишком велика и радиусы кривизны Rl, R2 изменяются вдоль меридиана достаточно плавно. Естественно предположить, что порядок величины перемещения 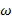 выше порядка величины перемещения и.
выше порядка величины перемещения и.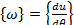 Тогда главные значения величин, определенных формулами (47) и (48), равны:
Тогда главные значения величин, определенных формулами (47) и (48), равны: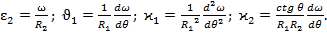 (54)
(54)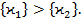 Поэтому можно считать, что
Поэтому можно считать, что (55)
(55) (56)
(56)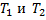 . Исключим из этих двух уравнений величину
. Исключим из этих двух уравнений величину 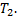 Умножим уравнение (53) на
Умножим уравнение (53) на 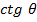 и сложим его с уравнением (52). Так как по условию
и сложим его с уравнением (52). Так как по условию 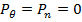 , получим
, получим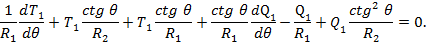
 , получим
, получим (57)
(57)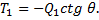 (58)
(58)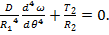 (59)
(59)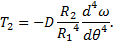
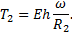
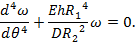
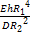 =12(1-
=12(1- 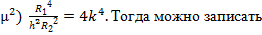
 (60)
(60) и коэффициент
и коэффициент 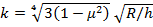 является постоянным большим числом (при
является постоянным большим числом (при 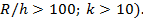
 (61)
(61)
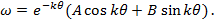
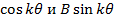 являются периодическими функциями угловой координаты
являются периодическими функциями угловой координаты 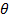 - по значению они не больше единицы. При увеличении угла
- по значению они не больше единицы. При увеличении угла 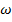 уменьшается в
уменьшается в 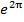 раз, т.е. становится пренебрежимо малой величиной. Длина отрезка меридиана, соответствующая этому периоду, равна
раз, т.е. становится пренебрежимо малой величиной. Длина отрезка меридиана, соответствующая этому периоду, равна
 Баки в различных расченых случаях нагружены: 1) давлением наддува р0; 2) давлением столба жидкости пхγН, где пх — осевая перегрузка; Н и у — соответственно высота столба и удельный вес жидкости; 3) силами реакции соседних отсеков.
Баки в различных расченых случаях нагружены: 1) давлением наддува р0; 2) давлением столба жидкости пхγН, где пх — осевая перегрузка; Н и у — соответственно высота столба и удельный вес жидкости; 3) силами реакции соседних отсеков.
 и Т2 в первую очередь определяет выбор того или иного конструктивного варианта бака и, как показывают соотношения (11.2) и (11.3), зависят от давления наддува р0.
и Т2 в первую очередь определяет выбор того или иного конструктивного варианта бака и, как показывают соотношения (11.2) и (11.3), зависят от давления наддува р0.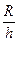
 которые оказываются расчетными (R — радиус обечайки бака; h — толщина стенки).
которые оказываются расчетными (R — радиус обечайки бака; h — толщина стенки).