
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Индуктивности и емкости в цепи переменного токаСодержание книги
Поиск на нашем сайте
Параллельное соединение электроприемников – основной вид соединений, так как в этом случае электроприёмники делаются на одно и то же напряжение. Параллельное соединение – это такой вид соединения, когда на всех элементах одно и то же напряжение, а ток в неразветвлённой части равен геометрической сумме токов этих элементов согласно первому закону Кирхгофа. Схема параллельного соединения R, xL, и xC приведена на рис. 3.16, а.
Рис. 3.16 Первый закон Кирхгофа в комплексном виде запишется следующим образом:
Выразим токи из закона Ома:
Для параллельного соединения элементов вводится понятие проводимости, величины, обратной сопротивлению, измеряемой в сименсах: · активная проводимость ·
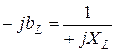 (См); (См);
· емкостная проводимость С учётом (3.32) выражение (3.33) примет следующий вид:
Выражение в квадратных скобках обозначим через Y и назовем полной или комплексной, проводимостью:
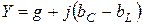 (См) (См)
Тогда закон Ома для параллельного соединения элементов в комплексном виде будет

где
Этой форме записи закона Ома соответствует схема замещения, показанная на рис. 3.16. Схемы а и б на рис. 3.16 являются эквивалентными. Построим векторную диаграмму для параллельного соединения резистора, индуктивности и емкости. Построение начинаем с комплексной плоскости (рис. 3.17, а). Параллельно оси действительных чисел (+ 1) строим вектор приложенного напряжения
Рис. 3.17 Если все стороны треугольника токов разделить на напряжение Проанализировав закон Ома для последовательного соединения (
Соотношение (3.38) показывает, что для каждого последовательного соединения элементов существует эквивалентное параллельное соединение этих же элементов. И наоборот: для каждого параллельного соединения элементов существует эквивалентное последовательное соединение этих же элементов. Соотношение (3.38) широко используется для преобразования сложных электрических цепей.
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 66; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.116.226 (0.01 с.) |
||||||||||||||||||||||||||||||||||||||||

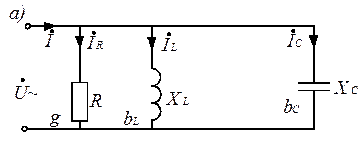

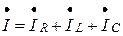 (3.32)
(3.32)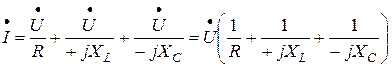 (3.33)
(3.33)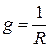 (См);
(См); (См).
(См). (3.35)
(3.35) (См)
(См)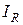 – активная составляющая тока;
– активная составляющая тока;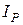 – реактивная составляющая тока.
– реактивная составляющая тока. , так как напряжение является общим для всех элементов. Далее по вектору напряжения
, так как напряжение является общим для всех элементов. Далее по вектору напряжения  (который совпадает по направлению с напряжением). Из конца вектора
(который совпадает по направлению с напряжением). Из конца вектора  (он опережает напряжение на угол 900). Из конца вектора
(он опережает напряжение на угол 900). Из конца вектора 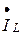 (он отстает от напряжения на угол 900), получаем точку «а». Соединив точку «а» с началом вектора тока в резисторе
(он отстает от напряжения на угол 900), получаем точку «а». Соединив точку «а» с началом вектора тока в резисторе 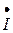 в неразветвлённой части, при этом образуется треугольник токов. Угол
в неразветвлённой части, при этом образуется треугольник токов. Угол 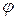 между вектором напряжения
между вектором напряжения 
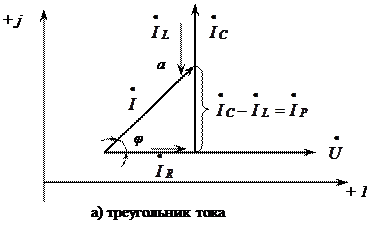

 , то получим подобный треугольнику токов треугольник проводимостей. Умножив стороны треугольника проводимостей на
, то получим подобный треугольнику токов треугольник проводимостей. Умножив стороны треугольника проводимостей на 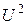 , получаем треугольник мощностей.
, получаем треугольник мощностей.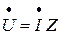 ) и для параллельного соединения (
) и для параллельного соединения (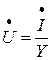 ), можно сделать вывод, что:
), можно сделать вывод, что: . (3.38)
. (3.38)


