
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Резистор в цепи однофазного переменного токаСодержание книги
Поиск на нашем сайте
Пусть в цепь переменного тока
Рис. 3.5
Падение напряжения на резисторе определим согласно закону Ома:
где Графики изменения тока i и падения напряжения uR показаны на рис. 3.6. Построим векторную диаграмму для цепи, содержащей резистивный элемент. Построение начнём с комплексной плоскости (рис. 3.7). Параллельно оси действительных чисел (+ 1) строим вектор действующего значения тока
Рис. 3.6
Далее, сравнивая законы изменения тока
Рис. 3.7
Поэтому закон Ома в комплексном виде запишется так:
Этой форме записи закона Ома соответствует схема замещения, показанная на рис. 3.5б. Мгновенная мощность на резисторе равна:
Из выражения (3.10) видно, что мгновенная мощность содержит постоянную составляющую Среднее значение мощности, выделяемой на резистивном элементе, равно:
где Мощность Р называется активной и измеряется в ваттах (Вт).
Индуктивность в цепи переменного тока (индуктивный элемент)
Пусть в цепь переменного тока
Рис. 3.8 Известно [1], что при прохождении тока через индуктивный элемент в нём возникает магнитный поток
где W – число витков катушки индуктивности. Эта ЭДС самоиндукции уравновешивается падением напряжения на индуктивности
Падение напряжения на индуктивности
Введём понятие индуктивного сопротивления
где f = 50 Гц. Графики изменения тока (
Рис. 3.9
Из рис. 3.9 следует, что ток Построим векторную диаграмму для цепи, содержащей индуктивность L. Построение начинаем с комплексной плоскости (рис. 3.10). Параллельно оси действительных чисел
Рис. 3.10
Теперь, сравнивая (рис. 3.9) законы изменения тока Закон Ома в комплексном виде для индуктивного элемента запишется
где
Мгновенная мощность индуктивности равна:
Мощность в цепи, содержащей индуктивный элемент, называют реактивной индуктивной мощностью (+ QL) и измеряют в вольт-амперах реактивных (вар).
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 43; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.66.242 (0.01 с.) |

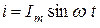 включен резистор R (рис. 3.5).
включен резистор R (рис. 3.5).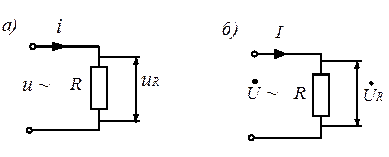
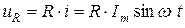 (3.8)
(3.8)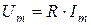 .
.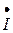 .
.
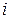 и падения напряжения
и падения напряжения 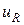 (рис. 3.6), делаем вывод: так как законы изменения тока
(рис. 3.6), делаем вывод: так как законы изменения тока  совпадает по направлению с вектором тока через резистор
совпадает по направлению с вектором тока через резистор 
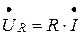 (3.9)
(3.9)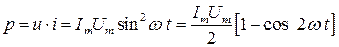 (3.10)
(3.10)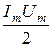 и переменную
и переменную 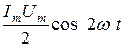 .
.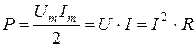 (Вт), (3.11)
(Вт), (3.11)
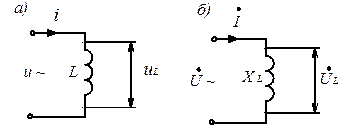
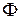 , который наводит в нем ЭДС самоиндукции
, который наводит в нем ЭДС самоиндукции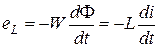 , (3.12)
, (3.12)
 (3.13)
(3.13)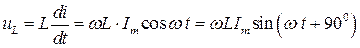 (3.14)
(3.14)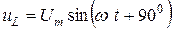
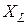
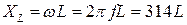 , (Ом) (3.15)
, (Ом) (3.15)
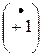 строим вектор действующего значения тока
строим вектор действующего значения тока 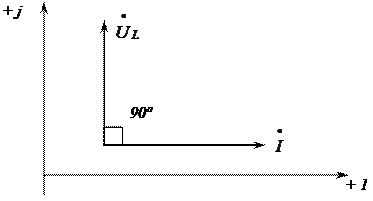
 и падения напряжения на индуктивности
и падения напряжения на индуктивности 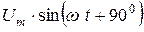 , делаем вывод, что вектор падения напряжения на индуктивности
, делаем вывод, что вектор падения напряжения на индуктивности 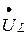 опережает вектор тока
опережает вектор тока 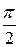 .
.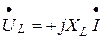 , (3.16)
, (3.16)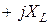 – комплекс индуктивного сопротивления;
– комплекс индуктивного сопротивления;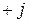 показывает, что вектор
показывает, что вектор 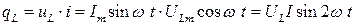 (3.17)
(3.17)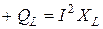 (вар) (3.18)
(вар) (3.18)


