Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проведение основных экспериментовСодержание книги Поиск на нашем сайте
Результаты предварительной возможности использования зависимости разности расходов воздуха от величины неплотности ЦПГ двигателя для ее оценки. После того как была выдвинута версия о возможности оценки технического состояния ДВС, в соответствии с планом проводились предварительные исследования в лабораторных условиях на экспериментальной установке. На стенд был установлен дизельный двигатель Д-240 (зав. № 422193). Исследования способа оценки технического состояния осуществляется следующим образом: к испытуемому двигателю подсоединяли устройства снятия сигналов. В форсуночные отверстия цилиндров двигателя устанавливались, с помощью специально разработанного приспособления, калибровочные шайбы одинаковой неплотности. Изменения относительной неплотностей ЦПГ производились сменой калибровочных шайб с заданной пропускной способностью. С помощью пускового устройства прокручивали коленчатый вал двигателя с заданной частотой вращения с отключением подачи топлива. Результаты эксперимента – средние значения по итогам измерений в параллельных опытах – приведены в таблице. 1. Из таблицы 1 видно, что разность расходов воздуха имеет выраженную зависимость от величины неплотности ЦПГ.
Таблица 1- Сравнительная оценка возможности диагностирования ДВС по величине разности расходов воздуха
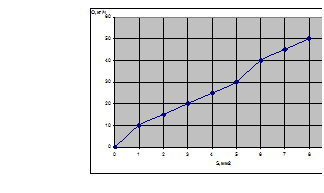
Графически эта зависимость изображена на рисунке 1.
Рисунок 1 Зависимость разности расходов воздуха от величины неплотности Статистическая обработка результатов исследований указанной зависимости проводилась с целью получения исходных данных для регрессионного анализа. Таким образом, зная разность расходов воздуха на впуске и выпуске можно оценить техническое состояние ЦПГ любого двигателя. Зависимость, приведённая на рисунке 1, логически завершают: предположения, высказанные в гипотезе исследования; теоретические выводы, результаты регрессионного анализа, наглядно иллюстрируют и подтверждают работоспособность способа оценки технического состояния двигателя по разности расходов. Предложенный способ защищён авторским патентом на изобретение. После эксперимента производили обработку опытных данных с помощью регрессионного анализа. Целью обработки экспериментальных данных является получение функциональной зависимости Результаты обрабатывали в соответствии с методикой, описанной в главе 3, в последовательности: Для каждой строки матрицы планирования по результатам всех параллельных опытов находили среднее арифметическое значение параметра оптимизации (отклика) и соответствующую каждому опыту дисперсию. Однородность ряда дисперсий проверяли с помощью критерия Кохрена - Все дисперсии признаны однородными, так как расчётное значение
Таблица 2 – Исходные данные для регрессионного анализа
Так как дисперсии
По результатам эксперимента вычислялись коэффициенты модели.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 77; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.26 (0.006 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

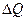 , л/мин
, л/мин
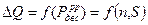 . Для построения математической модели используется регрессионный анализ.
. Для построения математической модели используется регрессионный анализ.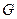 (при равномерном дублировании опытов), представляющего собой отношение максимальной дисперсии к сумме всех дисперсий.
(при равномерном дублировании опытов), представляющего собой отношение максимальной дисперсии к сумме всех дисперсий.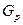 - критерия не превышает табличного значения
- критерия не превышает табличного значения 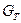 - критерия,
- критерия, 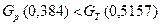 .
.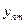 , л/мин
, л/мин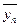 , л/мин
, л/мин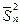
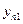
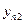
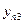
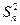 опытов однородны, то дисперсия воспроизводимости эксперимента
опытов однородны, то дисперсия воспроизводимости эксперимента 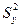 , вычисленная в соответствии с методикой (см.гл.3), будет равна:
, вычисленная в соответствии с методикой (см.гл.3), будет равна: