Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ:  Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия ЭкологияТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Графический метод решения задач линейногоСтр 1 из 7Следующая ⇒
ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Графический метод, как наиболее простой и наглядный, применяется преимущественно в целях уяснения сущности задач линейного программирования. Данный метод позволяет решать задачи только с двумя неизвестными. Для решения задач с большим числом неизвестных он неприменим, так как графические построения в многомерном пространстве без использования специальных графопостроителей на базе ЭВМ невозможны. Методика решения задач графическим методом предусматривает следующий порядок действий: 1. Постановка задачи. Предполагает словесную формулировку условий задачи и указание функции цели (на максимум или минимум). 2. Составление экономико-математической модели задачи. Данный этап решения задачи предусматривает математическую формулировку функции цели и условий задачи в виде системы неравенств. Форма записи условий задачи в виде системы неравенств называется стандартной. Геометрически каждое из неравенств представляет собой полуплоскость, которая может быть расположена по ту или иную сторону от распределительной прямой линии. 3. Вычисление координат точек пересечения граничных прямых и прямых функций цели с осями координат. Вычисление координат осуществляется в следующей последовательности: - каждое из неравенств, выражающих условия задачи (ограничения), заменяется уравнением. В геометрическом смысле полуплоскость заменяется прямой линией, математически выраженной в виде уравнения; - в каждом уравнении Х1 приравнивается к нулю (Х1=0) и по уравнению рассчитываются Х2 (Х2 в этом случае находится как отношение свободного члена в i на коэффициент при Х2). Затем Х2 приравнивается нулю (Х2=0) и определяется значение Х1. Полученные таким образом координаты точек пересечения граничных прямых (каждому уравнению соответствует своя прямая) с осями прямоугольных координат Х1 и Х2 заносят в специальную таблицу (см. таблицу 1.1); - целевая функция приравнивается к произвольному круглому числу (выражается в виде уравнения) с таким расчетом, чтобы получить координаты точек пересечения её прямой с прямоугольными осями координат Х1 и Х2 в пределах графика. Поочередно приравнивая Х1 и Х2 к нулю, как описано выше, вычисляются координаты точек пересечения, которые также заносятся в таблицу 1.1.
Для того, чтобы можно было на графике определить направление оптимизации, необходимо вычислить координаты точек пересечения второй прямой функции цели (Z 2) с осями координат Х1 и Х2. Данные координаты получают путем удвоения первоначального значения функции цели (Z 1) и значений полученных для нее координат. Координаты прямой также заносятся в таблицу 1.1. 4. Построение графика и установление области допустимых решений. График строится в следующей последовательности: - выбирается масштаб построения графика с учетом отражения на графике максимальных значений координат точек пересечения прямых с осями Х1 и Х2; - строятся оси прямоугольной системы координат Х1 (горизонтальная ось) и Х2 (вертикальная ось) и делается разбивка делений в соответствии с выбранным масштабом для каждой из осей; - на осях Х1 и Х2 откладываются координаты точек пересечения, полученные для соответствующего уравнения. Через данные точки проводится прямая. Если вычислена только одна координата точки пересечения, то это означает, что через данную точку пройдет прямая, параллельная другой оси координат. Аналогичным образом строятся прямые для всех уравнений и для двух значений функции цели (Z 1, Z 2); - после построения на графике граничных прямых относительно каждой из них устанавливается местоположение полуплоскости, содержащей допустимые решения для соответствующего ей неравенства. В каждое неравенство подставляются вместо неизвестных Х1 и Х2 значения начала оси координат, т.е Х1=0, Х2=0. Если подставленные значения удовлетворяют неравенству (т.е. соблюдается его смысл), то область допустимых решений (ОДР) расположена в той полуплоскости, которая находится от прямой со стороны начала координат. Если не удовлетворяют, то область допустимых решений находится с противоположной от начала координат стороны прямой. Направление расположения области допустимых решений относительно каждой из прямых показывается стрелкой в сторону расположения полуплоскости, удовлетворяющей условиям неравенства. В результате этого устанавливаются границы области допустимых решений (ограничивающие её прямые), а сама область штрихуется (рис. 1.1).
5. Поиск оптимального решения задачи. Поиск оптимального решения задачи осуществляется в следующей последовательности: - прямую, параллельно прямым Z 1 и Z 2 перемещают в направлении оптимизации (в ту сторону, в которой находится Z 2 по отношению к Z 1) до последней точки или грани касания с областью допустимых решений; - с графика снимаются координаты точки касания Z опт с областью допустимых решений. Они соответствуют оптимальным значениям неизвестных Х1 и Х2. Если же линия Z опт касается грани ОДР, то координаты любой точки грани являются оптимальным решением задачи. Это означает, что существует бесчисленное множество оптимальных решений, но при этом значение функции цели остается неизменным; - для контроля правильности решения задачи координаты точки оптимума (точки касания) подставляются в исходные неравенства. В результате данной постановки неравенства превращаются в равенства или сохраняют свой смысл; - оптимальные значения неизвестных подставляются в функцию цели, и вычисляется её оптимальное значение; - формулируется полный ответ решенной задачи.
ПРИМЕР РЕШЕНИЯ ЗАДАЧИ ГРАФИЧЕСКИМ МЕТОДОМ
При решении задачи сохраним нумерацию этапов решения, приведенную выше в методике. 1. Требуется определить в фермерском хозяйстве оптимальное соотношение посевных площадей пшеницы и гречихи. Под данные культуры фермер может отвести не более 120 га пашни. При этом фермером заключены контракты на гарантированную продажу партнерам не менее 1000 ц пшеницы и не менее 800 ц гречихи. Плановая урожайность пшеницы – 20 ц/га, гречихи – 25 ц/га. Закупочная цена 1 ц (условно): пшеницы – 5,0 тыс. руб., гречихи – 10,0 тыс. руб. Критерий оптимальности – максимум валовой продукции в стоимостном выражении.
2. В задаче примем следующие обозначения: Х1 - посевная площадь пшеницы, га; Х2 - посевная площадь гречихи, га. Сформулируем математически функцию цели и условия задачи в виде системы неравенств: Z =5,0∙20Х1+10,0∙25Х2→ max или Z =100Х1+250Х2→ max 1) Х1+ Х2≤120 – ограничение по площади пашни; 2) 20Х1≥1000 – ограничение по объёму производства пшеницы; 3) 25Х2≥800 - ограничение по объёму производства гречихи; Х1≥0; Х2≥0 – условие неотрицательности неизвестных.
3. Переходим от неравенств к уравнениям (от стандартной к канонической форме записи условий задачи) с целью последующего вычисления координат точек пересечения граничных прямых с осями координат Х1 и Х2. 1) Х1+ Х2=120 2) 20Х1=1000 3) 25Х2=800 Последовательно приравнивая Х1=0 и Х2=0 и подставляя их в уравнения, вычисляем координаты точек пересечения и заносим их в таблицу 1.1. Так, при Х1=0 в первом уравнении Х2=120 и т.д. по другим уравнениям. Целевой функции придаем произвольные значения 2000 и записываем её в виде уравнения: Z 1=100Х1+250Х2=2000. Подставляя поочередно в уравнение значения Х1=0 и Х2=0, получим координаты точек пересечения прямой Z 1 с осями координат. Удваивая значение функции цели Z 1 и её координат, получим значения функции цели Z 2 (4000) и её координаты. Заносим их в таблицу 1.1. Таблица 1.1 Координаты точек пересечения граничных прямых и прямых функций цели с осями координат Х1 и Х2
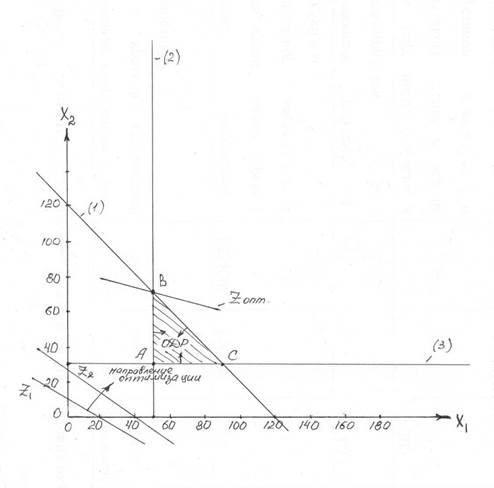
4. Строим график, откладывая на осях Х1 и Х2 в заданном координатами масштабе точки пересечения прямых. Через точки пересечения, относящиеся к соответствующему уравнению, проводим прямые (РИС. 1.1) с указанием номеров их уравнений (для граничных прямых) и символов (Z 1 и Z 2 – для прямых функций цели). Для определения на графике области допустимых решений (ОДР) подставим одновременно в первое неравенство значения, соответствующие началу координат (Х1=0, Х2=0). В результате этого получим, что 0≤120, т.е. неравенство сохраняет свой смысл. Следовательно, ОДР расположена от прямой (1) в направлении начала координат. Покажем это на графике стрелкой от данной прямой. Подставив Х1=0, Х2=0 во второе неравенство, видим, что неравенство не соблюдается (т.к. получаем 0≥1000). Следовательно, ОДР расположена в противоположной от начала координат стороне относительно прямой (2). То же самое имеем и для прямой (3). Таким образом, область допустимых решений находится в треугольнике АВС, образованном граничными прямыми.
5. Для поиска оптимального решения задачи ставим линейку на прямую Z 2, на графике и, сохраняя параллельность, двигаем в направлении оптимизации, указанном стрелкой, до последней точки касания с ОДР (до точки В). В точке В проводим на графике прямую Z опт, параллельную Z 2, и снимаем координаты точки оптимума (точки В): Х1 опт =50, Х2 опт =70. Для контроля правильности решения задачи подставим координаты точки оптимума (точки В) в исходные неравенства: 1) 50+70=120, согласно неравенству (1) должно быть ≤120; 2) 20∙50=1000, согласно неравенству (2) должно быть ≥1000; 3) 25∙70=1750, согласно неравенству должно быть ≥800. Следовательно, полученные координаты точки оптимума удовлетворяют всем неравенствам. Вычислим значение функции цели: Z опт =100Х1+250Х2=100∙50+250∙70=22500. Ответ: Оптимальным планом предусматривается отвести под пшеницу 50 га, под гречиху 70 га. В результате этого объем производства зерна пшеницы будет 1000 ц, гречихи 1750 ц. Стоимость валовой продукции составит 22500 тыс. руб.
Рис. 1.1. Область допустимых решений задачи
Задания для самостоятельной работы студентов по решению задач графическим методом представлены в приложении 1.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Перечислите основные этапы решения задач графическим методом. 2. В чем проявляется ограниченность практического применения графического метода? 3. Как определить область допустимых решений двумерной задачи на графике? 4. С какой целью неравенства преобразуются в равенства? 5. Объясните геометрический смысл неравенства и уравнения в двумерной задаче. 6. Как определяется на графике направление оптимизации? 7. При каких условиях оптимальное решение единственное, а при каких – их множество? Как изменяется при этом значение функции цели? 8. Как осуществлять контроль правильности решения задачи? 9. Что такое область допустимых решений? 10. Какое значение для решения задачи имеет расположение полуплоскости относительно граничной прямой? 11. В каком случае задача имеет бесчисленное число оптимальных решений при неизменном значении функции цели?
1800 | ||||||||||||||||||||||||||||||||
| II |
| 5 |
| 7 |
| 2 |
| 0 |
700 | ||||||||||||||||||||||||
| III |
| 6 |
| 8 |
| 9 |
| 0 |
1500 | ||||||||||||||||||||||||
| Потребности bj |
1600 |
1300 |
700 |
400 | 4000 4000 | ||||||||||||||||||||||||||||
В результате введения фиктивного потребителя (четвертую откормочную площадку с условной потребностью в зеленом корме в4=400 т) полностью сбалансированы между собой запасы (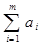
=4000 т) и потребности (
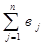=4000 т) в зеленом корме. Модель задачи стала закрытой.
В клетках на пересечении соответствующих строк и столбцов матрицы в правом верхнем углу проставляем расстояния (из таблицы 2.2) от поставщиков (полей) до потребителей (откормочных площадок). В клетках столбца фиктивного потребителя (четвертой площадки) расстояния равны 0, т.к. реально этого потребителя нет и зеленый корм не будет перевозиться и, кроме того, данная поставка не должна учитываться при расчете значений функции цели (произведение ХijСij =0).
4. Составление исходного допустимого базисного плана
Исходный план составляем на основе исходной матрицы путем распределения поставок груза (зеленого корма) по способу минимального элемента матрицы. В качестве таких элементов матрицы выступают ненулевые коэффициенты С ij (расстояния).
Минимальным коэффициентом матрицы является С2.3 =2, т.е. расстояние между II-м полем и 3-й площадкой. Следовательно, в клетку с номером 2.3 записываем наименьшую из поставок, расположенных по строке а 2 =700 и столбцу в3=700, на пересечении которых стоит клетка 2.3, т.е. Х 2.3 =700. Поскольку запасы а 2 =700 полностью исчерпаны при переносе данной поставки в клетку 2.3, то строка и столбец выбывают из дальнейшего рассмотрения, т.е. в клетках по данной строке а 2 и столбцу в3 не будет поставок (Х ij =0).
Следующий минимальный элемент матрицы расположен в клетке 1.1 С1.1 =3. Для этой клетки в качестве поставки выбираем наименьшее из чисел, стоящих по строке (а 1 =1800) и столбцу (в1=1600), на пересечении которых расположена данная клетка. Таким наименьшим числом является 1600, следовательно, поставка Х 1.1 =1600 и весь столбец (клетки 2.1 и 3.1) выбывает из дальнейшего рассмотрения поставок.
|
|
Однако по строке а 1 остается остаток 200 т, который размещаем в клетке 1.2. Следовательно, поставка Х 1.2 =200, а строка а 1 выбывает из дальнейшего рассмотрения поставок. Оставшуюся нераспределенной в столбце в2 поставку 1100 (1300-200=1100) заносим в единственно не выбывшую из рассмотрения клетку 3.2, т.е. Х 3.2 =1100. По строке а 3 оставшуюся нераспределенной поставку в4=400 записываем в клетку Х 3.4 =400.
Контроль правильности распределения поставок осуществляется следующим образом: суммы поставок (Х ij) по строкам матрицы должны быть равны запасам (а i), а по столбцам – потребностям (bj). Таким образом, исходный план составлен (таблица 2.4).
Таблица 2.4
Исходный план
| Поля севооборотов | Откормочные площадки | Запасы а i | |||||||
| 1 | 2 | 3 | 4 (фикт.) | ||||||
| I | 1600 | 3 | 200 | 6 |
| 4 |
| 0 |
1800 |
| II |
| 5 |
| 7 | 700 | 2 |
| 0 |
700 |
| III |
| 6 | 1100 | 8 | (0) | 9 | 400 | 0 |
1500 |
| Потребности bj |
1600 |
1300 |
700 |
400 | 4000 4000 | ||||
Далее необходимо проверить, является ли составленный план допустимым и базисным. Для этого подсчитываем число занятых поставками клеток (5) и сравниваем с цифрой, полученной по выражению m + n -1 (3+4-1=6). Поскольку число занятых клеток меньше, чем число, полученное по выражению m + n -1, то план вырожден, и следует для приведения его к базисному виду вводить нуль-поставку (0). Такую поставку разместим в клетке 3.3 (Х 3.3 =0), поскольку данная клетка не должна образовывать с другими занятыми клетками замкнутых контуров.
В результате введения нуль-поставки план стал допустимый, базисный и можно приступать к анализу его на оптимальность.
Значение целевой функции:
Z 1 =3∙1600+6∙200+2∙700+8∙1100=16200 т/км.
5. Анализ плана на оптимальность
Для проверки плана на оптимальность строим последовательно для свободных клеток плана замкнутые контуры и вычисляем их числовые характеристики (алгебраические суммы ∑ С ij со своими знаками).
Вершины контура, построенного для свободной клетки 1.3 разместятся в занятых клетках 1.2, 3.3 (условно занятая клетка нуль-поставкой) и 3.2. Вершине, расположенной в свободной клетке (1.3), присваивается знак «+», а остальным вершинам – поочередно чередующиеся знаки, продвигаясь в одном направлении по контуру (по часовой или против часовой стрелки). С учетом знаков и коэффициентов С ij, стоящих в занятых клетках, являющихся вершинами контура, вычисляем числовую характеристику: ∑ 1.3 =4–9+8–6=–3.
Аналогичным образом строим замкнутые контуры для других свободных клеток плана и вычисляем их числовые характеристики (∑ ij):
∑ 1.4 =0–0+8–6=2;
∑ 2.1 =5–2+9–8+6–3=7;
∑ 2.2 =7–8+9–2=6;
∑ 2.4 =0–0+9–2=7;
∑ 3.1 =6–8+6–3=1.
Одна из характеристик оказалась отрицательной, следовательно, план не оптимален и его необходимо улучшить.
6. Улучшение плана
Для улучшения плана производим перераспределение поставок
по контуру с отрицательной характеристикой ∑ 1.3 =–3.
Улучшаемый контур целесообразно вынести из плана и рассматривать отдельно (см. таблицу 2.5).
Таблица 2.5
Улучшение плана (контур клетки 1.3)
| 2 | 3 | |||
| I | 200- | 6 | (0)+ | 4 |
| II |
| 7 |
| 2 |
| III | 1100+ | 8 |
| 9 |
Поскольку наименьшей в отрицательной вершине контура оказалась нуль-поставка, то она перемещается в клетку 1.3, а клетка 3.3 становится свободной. Остальные поставки в вершинах данного контура остаются без изменения. Исходя из этого в улучшенном плане (таблица 2.6) по сравнению с исходным планом (таблица 2.4) переместится только нуль-поставка из клетки 3.3 в клетку 1.3. Величина изменения целевой функции ∆ Z 1 =–3х0=0, т.е. перемещение нуль-поставки не влечет за собой изменения величины целевой функции.
Улучшенный план является допустимым, базисным, т.к. число занятых клеток (6) соответствует выражению m + n -1 =6. Данный план заново анализируется на оптимальность (строятся контуры и вычисляются числовые характеристики, как и в предыдущем случае). В результате получены следующие характеристики (∑ ij):
∑ 1.4 =0–0+8–6=2;
∑ 2.1 =5–2+4–3=4;
∑ 2.2 =7–2+4–6=3;
∑ 2.4 =0–0+8–6+4–2=4;
∑ 3.1 =6–8+6–3=1;
∑ 3.3 =9–8+6–4=3.
Отсутствие отрицательных числовых характеристик свидетельствует, что план оптимален.
Таблица 2.6
Второй план
| Поля севооборотов | Откормочные площадки | Запасы а i | |||||||
| 1 | 2 | 3 | 4 (фикт.) | ||||||
| I | 1600 | 3 | 200 | 6 | 0 | 4 |
| 0 |
1800 |
| II |
| 5 |
| 7 | 700 | 2 |
| 0 |
700 |
| III |
| 6 | 1100 | 8 |
| 9 | 400 | 0 |
1500 |
| Потребности bj |
1600 |
1300 |
700 |
400 | 4000 4000 | ||||
Контроль правильности решения задачи
Вычислим значение целевой функции для оптимального плана:
Z опт =3∙1600+6∙200+2∙700+8∙1100=16200 т/км.
Контроль:
Z опт = Z 2 = Z 1 + ∆ Z 1 = 16200+0=16200 т/км.
Равенство значений целевой функции свидетельствует о правильном решении задачи. Особенностью данной задачи является то, что наглядно видно, как при улучшении плана путем перемещения нуль-поставки значение функции остается неизменным.
Ответ: Оптимальным для условий хозяйства будет следующее распределение поставок зеленого корма с полей севооборотов: с I поля 600 т на 1-ю площадку и 200 т – на 2-ю площадку; со II поля 700 т на 3-ю площадку; с III поля 1100 т – на 2-ю площадку и 400 т зеленой массы остается в резерве /излишек/, который может быть использован для производства сенажа. Общий тонно-километраж будет при этом наименьшим и составит 16200 т/км.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. В чем заключается постановка транспортной задачи?
2. Какие отличительные особенности постановки транспортных задач и какие показатели используются в качестве критериев оптимизации?
3. В чем заключается подготовка исходной информации для решения транспортных задач распределительным методом?
4. Какая модель задачи считается открытой и как привести ее к закрытому типу?
5. Как составляется исходный план в задачах распределительного типа?
6. Назовите признаки допустимого, недопустимого и базисного планов при решении задач распределительным методом.
7. Как преодолеть вырожденность плана в задачах распределительного типа?
8. Какие требования предъявляются к размещению нуль-поставок в матрице задачи?
9. В чем заключается отличие термина «открытая модель задачи» от термина «недопустимый план»?
10. Как выполняется анализ плана на оптимальность при решении задач распределительным методом?
11. Какой порядок построения замкнутых контуров в задачах, решаемых распределительным методом. Какие формы могут приобретать контуры?
12. По какому признаку определяется, оптимален ли план: если задача решается на минимум (Zmin); и если – на максимум (Zmax)?
13. Какой порядок улучшения плана?
14. Как выполняется контроль правильности решения задачи распределительным методом?
15. В чем проявляется ограниченность распределительного метода с точки зрения его широкого применения для решения практических задач в землеустройстве?
ПОТЕНЦИАЛОВ
Метод потенциалов представляет собой упрощенную модификацию распределительного метода, в котором предусматривается замена рассмотренного выше алгоритма распределительного метода в части «Анализ плана на оптимальность» на упрощенную процедуру, исключающую необходимость построения замкнутых контуров. Это обеспечивает методу потенциалов ряд преимуществ по сравнению с обычным распределительным методом: становится возможной реализация алгоритма метода на ЭВМ и, соответственно, решение задач с большим количеством поставщиков и потребителей.
Методика решения транспортной задачи методом потенциалов по этапам решения та же, что и в распределительном методе:
- постановка задачи;
- составление исходной матрицы;
- составление исходного допустимого базисного плана;
- анализ плана на оптимальность;
- улучшение плана;
- контроль решения задачи.
Однако этап «Анализ плана на оптимальность» имеет свой алгоритм, присущий только методу потенциалов. На данном этапе решения задачи выполняются следующие действия:
1. Вычисляются потенциалы α и β через коэффициенты С ij занятых клеток плана;
2. План анализируется на оптимальность через построение неравенств для свободных клеток плана;
3. Вычисляются числовые характеристики для неравенств, не отвечающих условиям оптимальности плана.
К вычислению потенциалов α и β приступают после составления исходного допустимого базисного плана по алгоритму распределительного метода.
Под потенциалами α и β понимаются относительные числа (оценки), выражающие в экономическом смысле, например, стоимость единицы перевозимого груза в i –м пункте отправления (потенциал α i) и в j -м пункте назначения (потенциал β j).
Вычисление потенциалов выполняются через коэффициенты С ij в занятых клетках плана по следующим формулам:
β j = α i + С ij, (2.8)
α i = β j - С ij, (2.9)
где α i – потенциал, относящийся к пункту отправления;
β j – потенциал, относящийся к пункту назначения;
С ij – коэффициент, выражающий, по условиям задачи, расстояние или стоимость перевозки единицы груза от i –го поставщика до j -го потребителя.
В матрице задачи для записи потенциалов α i выделяется дополнительный столбец, а для потенциалов β j дополнительная строка.
Вычисление потенциалов по формулам 2.8 и 2.9 можно начинать с любой строки (столбца). Однако при этом необходимо соблюдать следующую последовательность действий:
- исходному (первоначальному) значению α i (или β j) присваивается произвольное круглое число (10, 100 и т.д.) с таким расчетом, чтобы при вычислении потенциалов не было отрицательных чисел;
- выбор формулы расчета зависит от того, значение какого потенциала известно, а значение какого нужно определить. Например, если в качестве исходного задан потенциал α1 =10, то необходимо использовать формулу 2.8 для расчета недостающего потенциала β j. Если же известен потенциал β j, а следует определить значение потенциала α i, то используют формулу 2.9;
- вычисление потенциалов по формулам выполняется с использованием строки и столбца, на пересечении которых находится клетка, занятая поставкой. Если, например, занятая клетка стоит на пересечении первой строки и третьего столбца матрицы и известен исходный потенциал α1 =10, то через коэффициент С1.3 рассчитываем потенциал β3= α1+ С1.3=10+3=13. Если же по третьему столбцу стоит еще одна занятая клетка, но по другой строке, то для нее рассчитывается потенциал α i через уже найденное значение потенциала β3 и коэффициент данной клетки. Например, С3.3 =6, α1 = β3 – С3.3 = 13 – 6=7.
Аналогичным образом вычисляют все потенциалы α i и β j. После этого приступают к анализу плана на оптимальность.
Анализ плана на оптимальность выполняется путем построения неравенства для каждой свободной клетки плана и проверки их на соответствие следующим условиям:
α i + С ij ≥ β j (при решении задачи на минимум), или (2.10)
α i + С ij ≤ β j (при решении задачи на максимум) (2.11)
Признаком оптимальности плана служит соответствие всех неравенств, построенных для свободных клеток плана, типу неравенства, обусловленному функцией цели (на минимум или на максимум) решаемой задачи.
Если задача решается на минимум (Z → min), то все неравенства для свободных клеток должны быть типа 2.10. Если хоть одно из неравенств не соответствует данному типу (например, получилось ≤), то план не оптимален и нуждается в улучшении.
Для неравенств, которые не соответствуют требованиям оптимальности (формуле 2.10 или 2.11 в зависимости от функции цели в задаче) вычисляются характеристики, для последующего улучшения плана по формуле:
∑ ij = α i + С ij – β j (2.12)
Порядок улучшения не оптимального плана тот же, что и в распределительном методе.
Для контроля значение целевой функции можно вычислить по формуле:
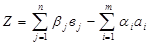(2.13)
ПРИМЕР РЕШЕНИЯ ЗАДАЧИ МЕТОДОМ ПОТЕНЦИАЛОВ
Для ясного понимания отличий метода потенциалов от обычного распределительного метода в качестве примера рассмотрим ту же задачу, что была решена распределительным методом. Постановка задачи, порядок составления исходной матрицы, составления исходного допустимого базисного плана являются общими для обоих рассматриваемых методов, поэтому продолжим решение данной задачи с этапа анализа плана на оптимальность.
Для этого в прежнем исходном плане (таблица 2.4) выделим столбец для записи потенциалов α i и строку – для потенциалов β j. Исходный план примет, следующий вид (таблица 2.7).
Таблица 2.7
Исходный план
| Поля севооборотов | α i | β j. | Откормочные площадки | Запасы а i | ||||||||
| 1 | 2 | 3 | 4 (фикт.) | |||||||||
| 13 | 16 | 1 | 8 | |||||||||
| I | 10 | 1600 | 3 | 200 | 6 | 0 | 4 |
| 0 | |||
1800
II
15
700
2
700
III
8
1100
(0)
9
400
1500
1600
1300
700
400
Вычислим потенциалы α i и β j. В качестве исходного примем потенциал α1 =10. Число 10 больше любого из значений коэффициентов С ij в исходном плане (максимальный коэффициент С3.3 =9), это исключает получение отрицательных значений при вычислении потенциалов.
Число 10 записываем в столбце α i по первой строке. По первой строке плана занятыми являются клетки 1.1 и 1.2. Рассчитываем потенциал β1 = α1 + С1.1 =10+3=13 и запишем его на свое место в исходном плане. Аналогичным образом определим потенциал β2 = α1 + С1.2 =10+6=16 и запишем его в столбец 2-го потребителя по строке I-го поля.
Через занятую клетку 3.2 в этом же столбце, где рассчитан уже потенциал β2 =16 рассчитываем для третьей строки плана потенциал α3.
Он рассчитывается: α3=β2–С3.2 =16–8=8. Запишем его в столбец α i по третьей строке. По третьей строке через С3.3 =9 и α3 =8 определяем потенциал β3 = α3 + С3.3 =8+9=17 и запишем его в столбец третьего потребителя. Аналогично рассчитываем β4 = α3 + С3.4 =8+0=8.
Оставшийся не рассчитанным потенциал α2 определяем:
α2=β3–С2.3 =17–2=15.
Следующим этапом является проверка исходного плана на оптимальность с помощью вычисленных потенциалов α i и β j. Поскольку функция цели в задаче ориентирована на минимум, то план будет анализироваться на оптимальность путем соответствия неравенств, построенных для свободных клеток плана, формуле 2.10.
Построим неравенства для свободных клеток плана:
1.3 α1 + С1.3≥ β3 10+4=14<17
1.4 α1 + С1.4≥ β4 10+0=10>8
2.1 α2 + С2.1≥ β1 15+5=20>13
2.2 α2 + С2.2≥ β2 15+7=22>16
2.4 α2 + С2.4≥ β2 15+0=15>8
3.1 α3 + С3.1≥ β1 8+6=14>13
Из приведенных выше расчетов видно, что для клетки 1.3 условие оптимальности плана не соблюдается, т.к. для нее α i + С ij < β j .
Следовательно, план не оптимален и его необходимо улучшить. Вычисляем характеристику для данной клетки:
∑1.3= α1 + С1.3- β3= 10+4–17=–3.
В результате проверки исходного плана на оптимальность установлено, что в улучшении нуждается клетка 1.3, т.е. та же, что и при решении данной задачи распределительным методом.
Порядок улучшения плана тот же, что и в распределительном методе.
В результате получаем улучшенный второй план, проверяем его на допустимость и базисность (путем соответствия числа занятых клеток выражению m + n -1).
Таблица 2.8
Второй план
| Поля севооборотов | α i | β j.
|
||
|
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 390; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.174.168 (0.294 с.) |
