Выпуклым многогранником называется такой многогранник, который лежит по одну сторону от плоскости любой его грани.

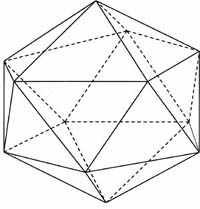
2. Все его грани – равные друг другу правильные многоугольники;

3. В каждой его вершине сходится одинаковое число ребер;

4. Все его двугранные углы равны.

Существует пять различных типов правильных многогранников, название которых пришли из Древней Греции:

Эдра – грань; тетра – четыре, гекса – шесть; окта – восемь; додека – двенадцать; икоса – двадцать.

- правильный тетраэдр (четырехгранник),

- правильный гексаэдр (куб) (шестигранник),

- правильный октаэдр (восьмигранник),

- правильный додекаэдр (двенадцатигранник),

- правильный икосаэдр (двадцатигранник).

 

Соотношение числа граней (Г), числа ребер (Р) и числа вершин (В) правильного многогранника соответствует следующей формуле (формула Эйлера):

Г + В = Р + 2

 

Правильные многогранники (тела Платона) – это такие выпуклые многогранники, все грани которых одинаковые правильные многоугольники и все многогранные углы при вершинах правильные и равные.

 

 

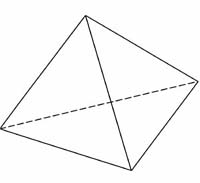
Рассмотрим эти многогранники:

Правильный тетраэдр

Правильный гексаэдр (куб)

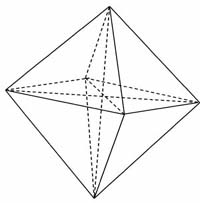
Правильный октаэдр

Правильный гексаэдр (куб)

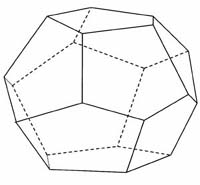
Правильный додекаэдр

Куб и октаэдр дуальны, то есть, получаются друг из друга, если центры тяжести граней одного принять за вершины другого и обратно.

Аналогично дуальны додекаэдр и икосаэдр.

Тетраэдр дуален сам себе.

Правильный додекаэдр получается из куба построением “крыш” на его гранях (способ Евклида), вершинами тетраэдра являются любые четыре вершины куба, попарно не смежные по ребру.

Так получаются из куба все остальные правильные многогранники.

Факт существования всего пяти действительно правильных многогранников удивителен – ведь правильных многоугольников на плоскости бесконечно много!

 

Все правильные многогранники были известны еще в Древней Греции, и им посвящена заключительная, XII книга знаменитых начал Евклида.

Эти многогранники часто называют так же платоновыми телами (телами Платона) в идеалистической картине мира, данной великим древнегреческим мыслителем Платоном.

Четыре из них олицетворяли четыре стихии:

- тетраэдр – огонь, - куб – земля, - икосаэдр – вода, - октаэдр - воздух;

- додекаэдр, символизировал все мироздание. Его по латыни стали называть quinta essentia (“пятая сущность”).

Придумать правильный тетраэдр, куб, октаэдр, по-видимому, было не трудно, тем более что этими формами обладают природные кристаллы, Как известно, правильные многогранники определяют форму кристаллических решеток некоторых химических веществ:

- куб – монокристалл поваренной соли (NaCl),

- октаэдр – монокристалл алюмокалиевых квасцов ((KAlSO₄)₂·l2H₂O).

- додекаэдр древние греки получили, рассматривая кристаллы пирита (сернистого колчедана FeS).

Имея же додекаэдр, нетрудно построить и икосаэдр: его вершинами будут центры 12 граней додекаэдра.

Где еще можно увидеть эти удивительные тела?

- икосаэдр точно передает форму одноклеточных организмов – феодарии.

Чем же вызвана эта природная геометризация? Может быть, тем, что из всех многогранников с таким же количеством граней именно икосаэдр имеет наибольший объем и наименьшую площадь поверхности. Это геометрическое свойство помогает морскому микроорганизму преодолевать давление водной толщи.

На рассмотренных примерах мы увидели, что правильные многогранники – самые выгодные фигуры. И природа этим широко пользуется.

 

Мы уже дали определение выпуклого многогранника: