
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электрические и магнитные цепиСодержание книги Поиск на нашем сайте ЭЛЕКТРИЧЕСКИЕ И МАГНИТНЫЕ ЦЕПИ ГЛАВА Т ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА Элементы, схемы электрических цепей и их классификация Сложность описания электрических цепей с большим многообразием реальных элементов (линий электропередачи, генераторов, трансформаторов и т.д.) привела к необходимости выделения некоторых идеализированных элементов, с помощью комбинаций которых можно описывать все реальные элементы. К идеализиро ванным элементам электрической цепи (рис. 1.2) относятся: источник ЭДС, источник тока, резистор, конденсатор и индуктив ная катушка. Для источника ЭДС (см. рис. 1.2, а) характерным является равенство напряжений между его выводами величине электродвижущей силы: иЬа = и = е; R, С и L этих элементов — соответственно сопротивлением резистора, емкостью конденсатора и индуктивностью катушки.
Выражение и = R ∙ I или i =
Устройство резистора
Противодействие проводника направленному движению зарядов (электрическому току) называется сопротивлением проводника. Устройство обладающее сопротивлением и используемое для ограничения силы тока в эл. цепи или приемнике эл. энергии называется резистором. Регулируемый резистор, включенный в электрическую цепь тока, называется реостатом.
Наряду с сопротивлением R резистор иногда характеризуют обратной величиной G = 1/ R называемой проводимостью. Единицей проводимости является сименс (1 См = 1 А/1 В). На схемах указывается одна из этих величин — сопротивление R или проводимость G. Введение проводимости иногда упрощает преобразования уравнений цепи, содержащей несколько резисторов.
Сопротивлением R можно охарактеризовать любой проводник длиной l и площадью сечения S (рис. 1.3). Если ток распределен по сечению проводника равномерно,
то Единицей удельного электрического сопротивления является Ом, умноженный на метр (Ом • м). В схеме замещения электрической цепи резистивные элементы отражают не только резисторы, но и сопротивления проводов линий электропередачи, сопротивления проводников, из которых выполнены обмотки трансформаторов и электрических машин, и т.п. Удельное электрическое сопротивление некоторых проводников при температуре 20 °С, мкОм • м, составляет: Серебро.................................................................................... 0,016 Медь....................::................................................................... 0,0175 Алюминий............................................................................... 0,029 Вольфрам................................................................................. 0,056 Сталь........................................................................................ 0,13...25 Константан, манганин.......................................................... 0,4...0,5 Нихром.................................................................................... 1,1
Конструктивно резисторы различных по номиналу и помощности а так же их назначения и могут сильно отличаться. Общим является использование в их конструкциях материалов с большим сопротивлением — константана, манганина и др.
Наряду с рассмотренными силовыми элементами в состав цепи могут входить также измерительные приборы, такие как амперметры (обозначаются буквой А в кружочке) для измерения токов и вольтметры (обозначаются буквой V в кружочке) для измерения напряжения. На рис. 1.11, а показана схема, содержащая один амперметр (для измерения тока i 1) и один вольтметр (для измерения напряжения u 2 = u 3). При правильном включении этих приборов не происходит изменения режима (т.е. не изменяются или почти не изменяются токи и напряжения элементов цепи). Это достигается за счет того, что внутреннее сопротивление амперметра R А очень мало, а внутреннее сопротивление вольтметра очень велико. Если же R А << R ВН, а R В >> R 3, то можно принять R А =0, R В = ∞,
Законы Кирхгофа
Наряду с компонентными уравнениями цепи для полного описания ее электромагнитных процессов применяют два закона Кирхгофа. Для любого узла справедлив первый закон Кирхгофа: алгебраическая сумма токов ветвей, соединенных с данным узлом, равна нулю. При этом ток, исходящий из узла, берется со знаком «плюс», а подходящий к узлу — со знаком «минус». Для узла I, изображенного на рис. 1.11, б, имеем - I 1 + I 2 + I 3 + 1 V = 0. Для любого контура (замкнутого пути, проходящего через несколько элементов) справедлив второй закон Кирхгофа: алгебраическая сумма напряжений на всех элементах контура равна нулю. Для практического использования этого закона необходимо задать определенные направления обхода контура, тогда напряжения элементов, совпадающие с направлением обхода, берутся со знаком «плюс», не совпадающие — со знаком «минус». Для одноконтурной схемы, изображенной на рис. 1.6, б, при обходе контура по часовой стрелке имеем - U + U 1 + U Н = 0. В общем случае, если число ветвей цепи равно В, а число узлов — У, то число независимых уравнений, которые можно составить по первому закону Кирхгофа, равно У - 1, а по второму: В - (У-1) = В -У+1. Таким образом, всего по законам Кирхгофа можно составить В уравнений. Дополнив эти В уравнения В-компонентными уравнениями, получим 2В уравнений, необходимых для определения В токов и В напряжений рассматриваемой схемы. Эти 2В уравнений называют полной системой уравнений схемы электрической цепи. Они позволяют решить задачу расчета (анализа) цепи — по заданной схеме и значениям параметров рассчитать неизвестные токи и напряжения ветвей. Для решения подобных сложных задач анализа разработаны специальные методы, которые будут рассмотрены далее.
Устройство конденсатора
Конденсатор (емкостной элемент) запасает энергию электрического поля:
его мгновенная мощность р= i ∙ u характеризует скорость изменения этой энергии во времени. Конденсатор выполняется в виде двух металлических пластин 1, 2, разделенных слоем диэлектрика 3 (рис. 1.4). Емкость, для использования которой и предназначен конденсатор, представляет собой отношение двух равных по величине, но противоположных по знаку зарядов пластин, разнесенных в пространстве, к напряжению этого элемента С= q/u. Единицей емкости является фарад (1 Ф =1Кл/В). Емкостью обладает не только конденсатор, но и пары проводов электропередачи, емкостью характеризуется связь каждого из этих проводов с землей. При составлении схемы замещения реальной цепи подобные связи заменяют емкостными элементами, входящими в схему наравне с конденсаторами. Устройство катушки
Индуктивная катушка (индуктивный элемент) запасает энергию магнитного поля:
ее мгновенная мощность р = i ∙ u характеризуется скоростью изменения этой энергии во времени. Конструктивно такая катушка выполняется из проводника в виде винтовой линии (рис. 1.5). Ток i создает магнитное поле, направление индукции которого показано стрелками. Полагая плотность индукции В одинаковой по сечению S катушки, магнитное поле можно охарактеризовать магнитным потоком Ф = В S. Произведение этого потока на число витков Таким образом, индуктивная катушка — элемент цепи, предназначенный для использования его индуктивности. Индуктивностью помимо катушек обладают и другие элементы реальных электрических цепей, в частности провода линий электропередачи, что необходимо отражать в схемах замещения соответствующих цепей.
Таким образом, любая часть реальной электрической цепи обладает всеми перечисленными параметрами (R, L, С), а резистор, конденсатор, катушка — элементы, в которых соответственно сопротивление, емкость и индуктивность являются основными параметрами, другими же их параметрами обычно пренебрегают.
Схема электрической цепи, состоящая из источника ЭДС е, резистора R, индуктивной катушки L и конденсатора С изображена на рис. 1.7, а. В схемах электрических цепей принято выделять ветви — последовательность элементов, имеющих один ток, и узлы — места соединения нескольких ветвей. Так, в схеме, представленной на рис. 1.7, а, можно выделить три ветви с токами i 1, i 2, i 3 соответственно и два узла I и 11. Электрические цепи классифицируют по типу электромагнитных процессов и типу элементов. По типу электромагнитных процессов электрические цепи подразделяют на цепи постоянного тока (если токи и напряжения всех элементов не изменяются во времени) и цепи переменного тока (если токи и напряжения изменяются во времени). Важным частным случаем цепей переменного тока являются цепи синусоидального тока (токи и напряжения таких цепей изменяются во времени по синусоидальному закону), которые будут рассмотрены в гл. 4. Наиболее простой класс цепей — цепи постоянного тока, поскольку в схемы их замещения не входят индуктивные катушки и конденсаторы. Из допущения о постоянстве тока из компонентного уравнения катушки и =
напряжение будет равно нулю, т.е. сама катушка в схеме замещения цепи на постоянном токе будет представлять собой идеальный проводник с нулевым сопротивлением — так называемую закоротку. Из допущения о постоянстве напряжения для конденсатора (см. рис. 1.2, г) из компонентного уравнения емкости
По типу элементов электрические цепи подразделяют на линейные и нелинейные. Цепь считается линейной, если все элементы линейны, т.е. их параметры (сопротивления, индуктивности, емкости, ЭДС, токи источников тока) не зависят от интенсивности процессов. Цепь считается нелинейной, если она содержит хотя бы один нелинейный элемент.
ГЛАВА 2. МАГНИТНЫЕ ЦЕПИ 2.1. Магнитное поле: основные понятия и величины Магнитное поле возникает всегда, когда имеются движущиеся электрические заряды или электрический ток. Часто магнитное поле возбуждается особыми веществами, называемыми постоянными магнитами. Чтобы использовать магнитное поле, надо знать его свойства. Основным свойством магнитного поля является силовое воздействие на движущиеся в нем заряженные тела или на проводники с током. Силовое воздействие зависит также от свойств вещества, вносимого в магнитное поле. Магнитное поле обладает определенной направленностью, оно характеризуется вектором. Обычно магнитные поля представляются с помощью силовых линий. Силовая линия магнитного поля является воображаемой линией, касательная к которой совпадает с индукцией магнитного поля В. Вектор У постоянных магнитов (или у намагниченных стержней) всегда имеется два полюса: N — норд (северный), откуда выходят силовые линии, и S — зюйд (южный), куда они входят. Если внести в магнитное поле магнитную стрелку, она всегда будет ориентирована по касательной к силовой линии, причем направление силовой линии показывает магнитный полюс N стрелки. Магнитное поле часто создается с помощью электрического тока I, протекающего по обмотке, например, соленоида. Солено идом называют катушку с сердечником из магнитного материала (рис. 2.3).
Образующееся в этом случае магнитное поле так же будет иметь два полюса. Направление магнитного поля (направление вектора индукции Магнитная индукция В определяет силовые свойства магнитного поля. Единицей измерения магнитной индукции является тесла (Тл). Для расчета магнитных полей применяют и другую физическую величину — напряженность магнитного поля H. Единицей напряженности магнитного поля является ампер на метр (А/м). Связь между индукцией и напряженностью магнитного поля в немагнитных материалах определяется выражением В =
Если силовые магнитные линии пронизывают некоторую поверхность площадью S, то используют понятие магнитного потока Ф через данную площадь: Ф= В∙ S. Единицей магнитного потока является вебер (Вб).
Магнитные свойства веществ Вещества, помещенные в магнитное поле, ведут себя по-разному. Такие вещества, как золото, серебро, медь, цинк и ряд других, незначительно ослабляют магнитное поле внутри вещества. Их называют диамагнетиками. Платина, магний, алюминий, хром, палладий, щелочные металлы, кислород и др. наоборот незначительно увеличивают магнитное поле. Они называются парамагнетиками. Вещества, в которых собственное (внутреннее) магнитное поле может в сотни и тысячи раз превосходить вызвавшее его внешнее поле, называются ферромагнетиками. К ним относятся железо (F е), кобальт (Со), никель (N1), некоторые редкоземельные элементы, а также сплавы на базе этих элементов. В электротехнике принято подразделять все вещества на магнитные (ферромагнетики) и немагнитные (диамагнетики и парамагнетики). Поскольку магнитное поле в немагнитных материалах практически не изменяется при воздействии внешнего поля, особый интерес вызывают ферромагнетики. Ферромагнетизм обусловлен наличием в веществе маленьких намагниченных областей — доменов, в которых магнитные моменты атомов имеют одно и то же направление. В принципе каждый домен является маленьким магнитом. Домены можно увидеть в не очень сильный микроскоп. Ферромагнетик состоит из большого числа доменов, которые при отсутствии внешнего магнитного поля ориентированы произвольным образом, так что ферромагнетик остается немагнитным. При помещении ферромагнетика во внешнее магнитное поле домены, направление которых близко к направлению силовых линий внешнего поля, начинают расти, а домены, намагниченные против внешнего поля, уменьшаются и, наконец, исчезают. При дальнейшем увеличении напряженности внешнего поля все домены устанавливаются вдоль силовых линий поля, наступает магнитное насыщение и намагниченность почти не растет. Если теперь уменьшить напряженность внешнего поля до нуля, то ориентация доменов нарушится лишь частично, поэтому намагниченность ферромагнетика уменьшается, но не до нуля. Чтобы уничтожить остаточную намагниченность образца, нужно приложить внешнее поле противоположного направления. Напряженность такого поля называется коэрцитивной силой Нс. Для каждого ферромагнетика существует температура, выше которой его ферромагнитные свойства исчезают. Она называется точкой Кюри. Для железа точка Кюри равна 768 °С, для никеля — 358 °С, а для кобальта - 1120°С. Для расчета индукции магнитного поля В в ферромагнетике используют выражение, которое учитывает способность к намагничиванию материала, В= Свойства ферромагнетиков намагничиваться учитываются
ГЛАВА 3 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА Основные понятия и характеристики Большинство электротехнических устройств предназначено для преобразования энергии, передачи энергии и информации на значительные расстояния. Все эти задачи проще решить с помощью переменных токов и напряжений. Переменные токи возникают в цепях с источниками переменного тока и с источниками переменных ЭДС. Переменными токами, напряжениями и ЭДС называются токи, напряжения и ЭДС, изменяющиеся с течением времени. Значения тока в произвольные моменты времени t называются мгновенными значениями тока и обозначаются i (t). Аналогично определяемые мгновенные значения напряжения и ЭДС обозначаются соответственно и(t) и е(t). Наиболее часто в технике применяются периодические токи, напряжения и ЭДС, значения которых повторяются периодически, т.е. через равные промежутки времени (рис. 4.1). Простейшим периодическим переменным током является синусоидальный (рис. 4.2), получивший широкое применение в электроэнергетике. Синусоидальные токи и напряжения обеспечивают наиболее экономичные режимы работы электротехнических устройств. Мгновенные значения синусоидальных токов i (t), напряжений и(t) и ЭДС е(t) математически описываются формулами где I
Угловая частота где f — частота синусоидальной функции; Т — период синусоидальной функции — минимальный промежуток времени, через который мгновенные значения синусоидальной величины повторяются. В системе СИ время t и период T выражаются в секундах (с), частота В энергоустановках автономных объектов (речные и морские суда, самолеты, вертолеты и т.д.) используются частоты 200, 400, 1000 Гц. Радиовещание, радиосвязь, телевидение, радиолокация используют частоты до 10- 1010 Гц и выше. Единицей угловой частоты Аргумент синусоидальной функции ( Разность начальных фаз двух синусоидальных токов и напряжений Если
Если Переменный ток i (t) характеризуют по его действующему значению I, равному среднеквадратическому значению переменного тока: I = Численно действующее значение переменного тока равно такому значению постоянного тока, при котором выделяется за один период такое же количество теплоты, как и при данном переменном токе:
В случае синусоидального тока: Отсюда действующее значение синусоидального тока Смысл вычисления действующего значения синусоидальных токов объясняет рис. 3.3. ЗАПОМНИТЕ При изображении синусоидальных эдс, напряжений и токов из начала координат проводят векторы, равные амплитудным значениям этих величин, под углом к горизонтальной оси. Положительные углы Совокупность векторов на плоскости, изображающих эдс, напряжения и токи одной частоты, называют векторной диаграммой. При исследовании установившихся режимов векторы неподвижны, их длина равна действующим значениям электрических величин. С помощью векторов можно производить геометрическое суммирование электрических величин. Так, на рис. 25, в показаны векторы токов Векторные диаграммы широко используют при анализе электрических цепей переменного тока. ЗАПОМНИТЕ Сопротивление резистора из-за явлений вытеснения тока к поверхности проводника несколько возрастает и тем больше, чем больше частота тока в резисторе. При переменном напряжении на зажимах конденсатора в диэлектрике, заключенном между его электродами, электрическая энергия преобразуется в энергию электрического поля и запасается. Нельзя себе представить ток без магнитного поля так же, как и магнитное поле без тока. Это в равной степени относится как к постоянному, так и переменному токам. При переменном токе переменным будет и магнитный поток, следовательно, в каждом элементе электрической цепи будет наводиться эдс самоиндукции, будет накапливаться энергия и, наконец, преобразование электрической энергии в тепловую, как необратимый процесс, происходит непрерывно во всех элементах электрической цепи. При этом не только резисторы, но и катушки индуктивности, а также конденсаторы обладают электрическим сопротивлением и при наличии тока в них происходит выделение теплоты. ► Таким образом, все элементы электрической цепи обладают одновременно: индуктивностью В реальной цепи на одном каком-либо участке, например в конденсаторе, преобладает электрическое поле; в катушках индуктивности преобладает магнитное поле. Поэтому, отвлекаясь от действительной картины сложных физических явлений, будем считать, что, например, резистор в цепи переменного тока обладает активным сопротивлением и для него пренебрежимо малы В двух других элементах ( ЭЛЕКТРИЧЕСКИЕ И МАГНИТНЫЕ ЦЕПИ ГЛАВА Т
|
|||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 153; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.014 с.) |


 называется законом Ома для участка цепи, I =
называется законом Ома для участка цепи, I = 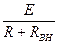 закон Ома для полной цепи, (учитывается внутреннее сопротивление источника), а произведение мгновенных значений напряжения и и тока i называется мгновенной мощностью р = i ∙ u, R ∙ i 2 – это для резистора.Мощность в данном случае определяет количество теплоты, выделяемой резистором в единицу времени. Таким образом, резистор (резистивный элемент) — это элемент, предназначенный для использования его электрического сопротивления. Единицей сопротивления является ом (1 Ом= 1 В/1 А), единицей мгновенной мощности — ватт (1 Вт = 1 В • 1 А).
закон Ома для полной цепи, (учитывается внутреннее сопротивление источника), а произведение мгновенных значений напряжения и и тока i называется мгновенной мощностью р = i ∙ u, R ∙ i 2 – это для резистора.Мощность в данном случае определяет количество теплоты, выделяемой резистором в единицу времени. Таким образом, резистор (резистивный элемент) — это элемент, предназначенный для использования его электрического сопротивления. Единицей сопротивления является ом (1 Ом= 1 В/1 А), единицей мгновенной мощности — ватт (1 Вт = 1 В • 1 А).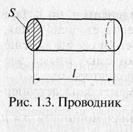

 Условное обозначение резисторов на схеме (нерегулируемый и регулируемый);
Условное обозначение резисторов на схеме (нерегулируемый и регулируемый);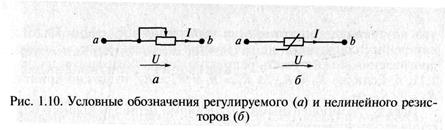
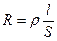 , —, где
, —, где 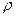 — удельное электрическое сопротивление, характеризующее свойства материала проводника.
— удельное электрическое сопротивление, характеризующее свойства материала проводника.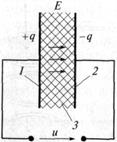
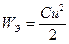 ;
;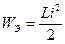
 катушки называют потокосцеплением
катушки называют потокосцеплением 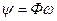 . Индуктивность характеризует связь между потокосцеплением и вызывающим его током:
. Индуктивность характеризует связь между потокосцеплением и вызывающим его током:  . Единицей магнитного потока является тесла (1 Тл = 1 Вб ∙1м2, единицей индуктивности — генри (1 Гн = 1 Тл/1 А).
. Единицей магнитного потока является тесла (1 Тл = 1 Вб ∙1м2, единицей индуктивности — генри (1 Гн = 1 Тл/1 А).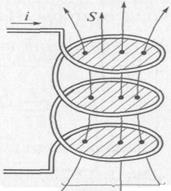
 (см. рис. 1.2, д) следует, что ее
(см. рис. 1.2, д) следует, что ее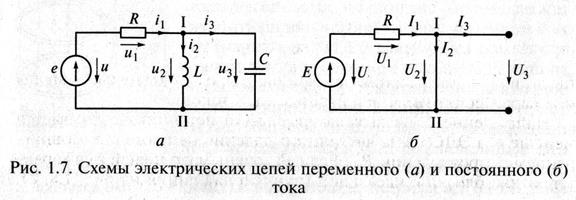
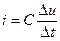 следует, что ток этого элемента равен нулю, а сам элемент будет представлять в схеме замещения на постоянном токе разрыв ветви. Таким образом, схеме электрической цепи переменного тока (рис. 1.7, а) при постоянном токе будет соответствовать схема замещения (рис. 1.7, б).
следует, что ток этого элемента равен нулю, а сам элемент будет представлять в схеме замещения на постоянном токе разрыв ветви. Таким образом, схеме электрической цепи переменного тока (рис. 1.7, а) при постоянном токе будет соответствовать схема замещения (рис. 1.7, б). совпадает с положением магнитной стрелки магнитного компаса (рис. 2.1). Магнитные силовые линии всегда замкнуты. На рис. 2.1 показаны силовые линии постоянного магнита, а на рис. 2.2 — магнитное поле проводника с током.
совпадает с положением магнитной стрелки магнитного компаса (рис. 2.1). Магнитные силовые линии всегда замкнуты. На рис. 2.1 показаны силовые линии постоянного магнита, а на рис. 2.2 — магнитное поле проводника с током.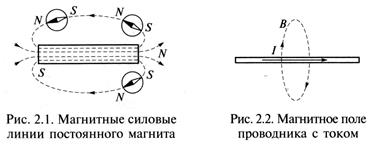

 , где
, где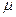 0 — магнитная постоянная, равная
0 — магнитная постоянная, равная  . Напряженность
. Напряженность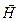 также является векторной величиной и совпадает по направлению с вектором индукции
также является векторной величиной и совпадает по направлению с вектором индукции  ,
, 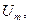 Ет — амплитудные значения тока, напряжения и ЭДС;
Ет — амплитудные значения тока, напряжения и ЭДС; 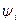 ,
, 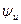 ,
, 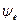 , — начальные фазы тока, напряжения и ЭДС.
, — начальные фазы тока, напряжения и ЭДС.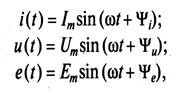
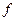 = 2л / Т,
= 2л / Т, +
+  ) называют текущей фазой. Фаза (
) называют текущей фазой. Фаза ( называется сдвигом по фазе.
называется сдвигом по фазе. 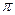 = ±180°, то о таких напряжениях и токах говорят, что они находятся в противофазе. Если
= ±180°, то о таких напряжениях и токах говорят, что они находятся в противофазе. Если 
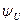 -
- 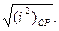
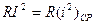
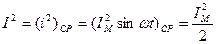
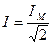 . Аналогично действующие значения синусоидальных напряжения
. Аналогично действующие значения синусоидальных напряжения  и ЭДС
и ЭДС 
 .Проекция вращающегося вектора на ось ординат (ось мгновенных значений) равна мгновенному значению синусоидальной величины (эдс, напряжения, тока).
.Проекция вращающегося вектора на ось ординат (ось мгновенных значений) равна мгновенному значению синусоидальной величины (эдс, напряжения, тока).
 и
и 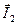 , а также вектор их геометрической суммы
, а также вектор их геометрической суммы 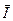 =
=  ,
, 
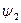 , и
, и 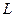 , емкостью С и электрическим сопротивлением
, емкостью С и электрическим сопротивлением 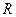 .
.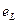 и ес, направленных против приложенного к этим элементам напряжения. Поэтому элементы L и С в электрической цепи переменного тока называют реактивными, а их способность противодействовать переменному току, называют реактивным сопротивлением элементов. Для элемента L, это сопротивление называют индуктивным и обозначают Х L, для элемента С — емкостным сопротивлением и обозначают Хс
и ес, направленных против приложенного к этим элементам напряжения. Поэтому элементы L и С в электрической цепи переменного тока называют реактивными, а их способность противодействовать переменному току, называют реактивным сопротивлением элементов. Для элемента L, это сопротивление называют индуктивным и обозначают Х L, для элемента С — емкостным сопротивлением и обозначают Хс


