
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правильную интерпретацию волновой функции дал в 1926 Г. М. Борн.
По Борну:
Квадрат модуля волновой функции определяет вероятность (dP) того, что частица будет обнаружена в пределах объема dV. По волновому закону меняется не сама вероятность, а амплитуда вероятности: Ψ(x, y, z, t).
(48.5) – условие нормировки. Функции, удовлетворяющие условию (48.5), называют нормированными.
Стандартные условия, которым должна удовлетворять волновая функция:однозначность, непрерывность, конечность (за исключением, быть может, особых точек). Кроме того, непрерывность и конечность первой производной. Из физического смысла волновой функции следует, что квантовая механика имеет статистический характер. С помощью волновой функции можно предсказать, с какой вероятностью частица может быть обнаружена в различных точках пространства. В квантовой механике состояние микрочастиц описывается с помощью функции Ψ(x, y, z, t). Волновая функция - Ψ является основным носителем информации об их корпускулярных и волновых свойствах.
Уравнение Шрёдингера
В 1926 г. развивая идеи де Бройля о волновых свойствах вещества, Шрёдингер получил свое уравнение. Оно позволяет найти волновые функции частиц, движущихся в различных силовых полях.
где m - масса частицы, i - мнимая единица, U - потенциальная энергия, Δ - оператор Лапласа. Результат действия оператора Лапласа на некоторую функцию представляет собой сумму вторых частных производных по соответствующим координатам:
Из (49.1) следует, что вид волновой функции Ψ(x, y, z, t) определяется функцией U, т.е. характером сил, действующих на частицу. Уравнение Шредингера является основным уравнением релятивистской механики. Оно не может быть выведено из других соотношений. Шредингер установил свое соотношение, исходя из оптико-механической аналогии. Для одномерного случая уравнение Шредингера имеет вид:
Это уравнение (49.3) совпадает c уравнением (48.1), если U =0. Если же частица движется в силовом поле, характеризуемом потенциальной энергией U, то энергия и импульс связаны соотношением:
Уравнение Шрёдингера в этом случае имеет вид:
Для стационарного силового поля (постоянного во времени)
где E – полная энергия частицы. Тогда дифференциальное уравнение принимает вид:
Сократив на общий множитель exp[-i(E/ħ)t], придем к дифференциальному уравнению, определяющему функцию φ:
Уравнение (49.8) называется – уравнением Шредингера для стационарных состояний. Это уравнение часто записывают в виде (49.9):
В случае стационарного силового поля волновая функция имеет вид (49.6), и тогда:
плотность вероятности равна
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 81; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.77.114 (0.006 с.) |
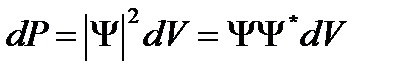 .
.
 .
.
 – плотность вероятности нахождения частицы в соответствующем месте пространства.
– плотность вероятности нахождения частицы в соответствующем месте пространства.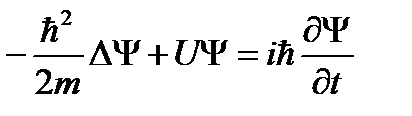 ,
,
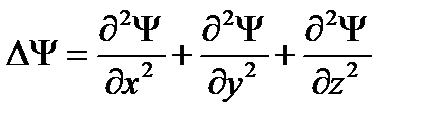 .
.
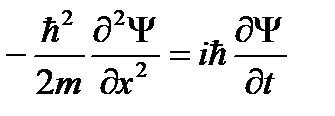 .
.

 .
.
 не зависит от t, тогда:
не зависит от t, тогда: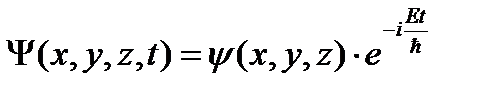 ,
,
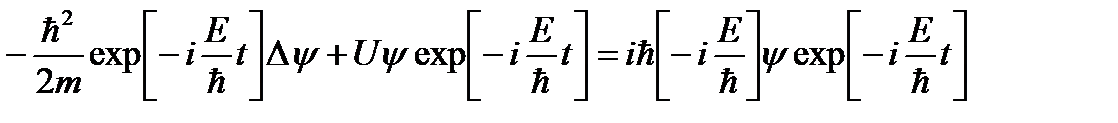 .
.
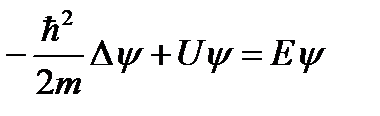 .
.
 .
.
 ,
,
 и, следовательно, от времени не зависит.
и, следовательно, от времени не зависит.


