
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предикаты и операции над нимиСодержание книги Поиск на нашем сайте
Введем основное понятие данной главы. Определение. Пусть М – непустое множество. Тогда nместным предикатом, заданным на М, называется выражение, содержащее n переменных и обращающееся в высказывание при замене этих переменных элементами множества М. Рассмотрим примеры. Пусть М есть множество натуральных чисел N. Тогда выражения “ x – простое число”, “ x – четное число”, “ x больше 10” являются одноместными предикатами. При подстановке вместо x натуральных чисел получаются высказывания: “2 – простое число”, “6 – простое число”, “3 – четное число”, “5 больше 10” и т.д. Выражения “ x больше y ”, “ x делит y нацело”, “ x плюс y равно 10” являются двухместными предикатами. (Конечно, последнее выражение можно было записать и так: “ x + y =10”.) Примеры трехместных предикатов, заданных на множестве натуральных чисел: “число z лежит между x и y ”, “ x плюс y равно z ”, “| x – y | ≤ z ”. Будем считать, что высказывание есть нульместный предикат, то есть предикат, в котором нет переменных для замены. Надо отметить, что местность предикатов не всегда равна числу всех переменных, содержащихся в выражении. Например, выражение “существует число x такое, что y = 2 x ” на множестве натуральных чисел определяет одноместный предикат. По смыслу этого выражения в нем можно заменять только переменную y. Например, замена y на 6 дает истинное высказывание: “существует число x такое, что 6 = 2 x ”, а замена y на 7 дает ложное (на множестве N) высказывание: “существует число x такое, что 7 = 2 x ”. Предикат с заменяемыми переменными x 1, …, xn будет обычно обозначаться заглавной латинской буквой, после которой в скобках указаны эти переменные. Например, P (x 1, x 2), Q (x 2, x 3), R (x 1). Среди переменных в скобках могут быть и фиктивные. На совокупности всех предикатов, заданных на множестве М, вводятся знакомые операции конъюнкция, дизъюнкция, отрицание, импликация и эквиваленция. Эти операции вводятся довольно очевидным образом. Приведем в качестве примера определение конъюнкции предикатов. Определение. Предикат W (x 1, …, xn) называется конъюнкцией предикатов U (x 1, …, xn) и V (x 1, …, xn), заданных на множестве M, если для любых а 1, …, an из М высказывание W (a 1, …, an) есть конъюнкция высказываний U (a 1, …, an) и V (a 1, …, an). Легко по аналогии привести определения и других упомянутых выше операций. В логике предикатов первого порядка вводятся и две новые операции. Называются они навешиванием квантора общности и навешиванием квантора существования. Эти операции рассмотрим вначале на примерах. Пусть дано выражение “существует x такой, что x + y = 10”. На множестве натуральных чисел это предложение определяет одноместный предикат P (y), так Р(2) и Р(9) – истинные высказывания, Р(11) – ложное. Если обозначить предикат “ x + y = 10” через S (x, y) (а это предикат двухместный), то P (y) можно записать так: “существует х такой, что S (x, y)”. В этом случае говорят, что предикат P (y) получен из предиката S (x, y) навешиванием квантора существования на x и пишут P (y) = (∃ x) S (x, y). Рассмотрим другой пример. Выражение “для всех х справедливо, что y ≥ –х2” определяет на множестве целых чисел одноместный предикат Q (y). Если предикат “ y ≥ –х2” обозначить через T (x, y), то Q (y) можно записать так: “для всех x справедливо T (x, y)”. В таком случае говорят, что предикат Q (y) получен из предиката T (x, y) навешиванием квантора общности на х и пишут Q (y) = (∀ x) T (x, y). После этих примеров нетрудно дать определение в общем виде. Определение. Пусть P (x 1, …, xn) – предикат, заданный на множестве M, y – переменная. Тогда выражение “для всякого y выполняется P (x 1, …, xn)” – предикат, полученный из P навешиванием квантора общности на переменную y, а выражение “существует y такой, что выполняется P (x 1, …, xn)” – предикат, полученный из P навешиванием квантора существования на переменную y. Обозначения этих операций были введены выше. Заметим, что в определении не требуется, чтобы переменная y была одной из переменных x 1, …, xn, хотя в содержательных примерах, которые будут приведены ниже, квантор будет навешиваться на одну из переменных x 1, …, xn. Указанное требование не налагается в определении, чтобы избежать усложнения определения формулы логики предикатов. Если y – одна из переменных x 1, …, xn, то после навешивания квантора на переменную y новый предикат является (n –1)-местным, если же y ∉ { x 1, …, xn }, то местность нового предиката равна n. Если предикат W (x 1, …, xn) получен из предикатов U (x 1, …, xn) и V (x 1, …, xn) с помощью связок, то истинность высказывания W (a 1, …, an) определяется таблицами истинности этих связок. Пусть W (x 1, …, xn) = (∀ y) U (x 1, …, xn, y). Тогда высказывание W (a 1, …, an) истинно тогда и только тогда, когда для любого b ∈ M истинно высказывание U (a 1, …, an, b). Если же W (x 1, …, xn) = (∃ y) U (x 1, …, xn, y), то высказывание W (a 1, …, an) истинно в том и только в том случае, когда найдется b ∈ M, для которого высказывание U (a 1, …, an, b) истинно. Понятие предиката – весьма широкое понятие. Это видно уже из приведенных выше примеров. Расширим запас таких примеров, показав, что n -местная функция может рассматриваться как (n +1)-местный предикат. Действительно, функции y = f (x 1, …, xn), заданной на множестве M, можно поставить в соответствие выражение “ y равно f (x 1, …, xn)”. Это выражение есть некоторый предикат P (x 1, …, xn, y). При этом, если элемент b есть значение функции в точке (a 1, …, an), то высказывание P (a 1, …, an, b) истинно, и обратно. (Подобное “превращение” функции в предикат мы уже делали выше для сложения натуральных чисел.) На предикаты можно смотреть и более формально, причем с двух точек зрения. Во-первых, предикат можно представить отношением следующим образом. Пусть предикат P (x 1, …, xn) задан на множестве M. Рассмотрим прямую степень этого множества Mn = M × M ×…× M и подмножество Dp множества Mn, определяемое равенством: Dp = {(a 1, …, an)∈ Mn ⏐высказывание P (a 1, …, a n) истинно}. Отношение Dp можно назвать областью истинности предиката P. Во многих случаях предикат P можно отождествить с отношением Dp. При этом, правда возникают некоторые трудности при определении операций над отношениями, аналогичных операциям над предикатами. Во-вторых, предикат P (x 1, …, xn), заданный на M, можно отождествить с функцией fp: Mn →{0, 1}, определяемой равенством
fp (a 1, …, an) = 0 в противном случае. Мы, в основном, будем понимать термин “предикат” в смысле исходного определения, т.е. как языковое выражение. Связано это с тем, что одной из главных целей, как уже отмечалось во введении, является изучение выразительных возможностей логики первого порядка, возможности представления средствами этой логики информации, выраженной на естественном (скажем, русском) языке.
|
||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 158; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.207.115 (0.007 с.) |

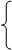 1, если P (a 1, …, an) истинно,
1, если P (a 1, …, an) истинно, 


