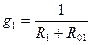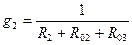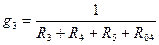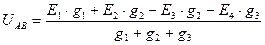Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод узловых и контурных уравненийСодержание книги
Поиск на нашем сайте
1. В схеме 3 ветви Для решения задачи надо составить 3 уравнения.
2. (n – 1) уравнение составляем по I закону Кирхгофа. n – число узлов схемы I 1 + I 2 – I = 0.
3. Недостающие для решения задачи уравнения составляем по II закону Кирхгофа, выбираем контуры и направления их обхода (произвольно) Е 1 – Е 2 = I 1· R 01 – I 2 · R 02 Е 1 = I 1· R 01 + I · R
4. Получили систему из 3-х уравнений с тремя неизвестными
Подставляем данные задачи
5. Решаем систему уравнений и получаем I 1 = 10 A I 2 = –5 A I 3 = 5 A
6. Ток I 2 имеет знак «–», это означает, что реальное направление тока противоположно выбранному. На схеме изменяем направление тока.
7. Решение задачи можно проверить по уравнению баланса мощностей: сумма мощностей всех генераторов электрической цепи равна сумме мощностей всех потребителей.
Таким образом, E 1 I 1 = E 2 I 2 + Подставляем численные значения и получаем 1300 Вт = 1300 Вт, т.е. задача решена верно.
Последовательное, параллельное и смешанное соединения резисторов. Метод «свёртки» Последовательное соединение R 1 R 2 I R 3
U
При последовательном соединении конец первого резистора соединен с началом второго, конец второго с началом третьего и т.д.
Свойства:
Параллельное соединение I
I 1 I 2 I 3
U R 1 R 2 R 3
При параллельном соединении элементы включены так, что имеют две общие точки. Свойства:
Смешанное соединение При смешанном соединении имеются участки с последовательным и параллельным соединением.
1. Направляем и обозначаем токи, начиная от «+» источника. 2. Решаем задачу методом «свертки», т.е. последовательно заменяем сопротивление отдельных участков их эквивалентными. Находим эквивалентные сопротивления всей цепи. а) R 2 и R 3 соединены параллельно
б) R 1, R 23 и R 4 соединены последовательно R ЭКВ = R 1 + R 23 + R 4
3. Определяем общий ток
I 1 =
4. Для того, чтобы определить токи I 2 и I 3, определим напряжение между узлами А и В. U AB = I 1· R 23 или U AB = E – I 1(R 1 + R 4 + R 0).
5. Находим токи 6. Проверяем решение, применяя I закон Кирхгофа: I 1 = I 2 + I 3.
Вопросы на динамику в электрической цепи: ?: Как изменится U AB, если R 1 увеличится? Ответ: R 1 ↑ R ЭКВ↑ I 1↓ U AB = I 1· R 34 уменьшится.
?: Как изменится U AB, если R 3 уменьшится? Ответ: R 3 ↓ R 34↓ R ЭКВ↓ I 1↑
U AB = Е – I 1 (R 1 + R 4 + R 0) уменьшится. Метод узлового напряжения Формулы основаны на законах Кирхгофа. Метод можно применить для расчета схемы, имеющей 2 узла.
В
R 01 R 02 R 03
Токи надо направить во всех ветвях в одну сторону, например, от узла А к узлу В. Находим проводимости всех ветвей
Находим узловое напряжение
Узловое напряжение равно алгебраической сумме произведений ЭДС и проводимостей ветвей, деленной на сумму проводимостей всех ветвей. ЭДС входит в формулу со знаком «+», если ее направление совпадает с направлением тока, в противном случае ей присваивают знак «–». Определяем токи ветвей по формулам: I 1 = (Е 1 – U AB) g 1 I 2 = (Е 2 – U AB) g 2 I 3 = (Е 3 – U AB) g 3 I = – U AB· g Решим задачу в общем виде, применяя метод узлового напряжения
Проводимость ветви – величина, обратная ее эквивалентному сопротивлению.
I 1 = (Е 1 – U AB)· g 1 I 2 = (Е 2 – Е 3 – U AB)· g 2 I 3 = (– Е 4 – U AB)· g 4
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-20; просмотров: 104; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.122.96 (0.009 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


 E 1 E 2
E 1 E 2





 I 1 I 2
I 1 I 2

 I
I


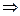 необходимо найти 3 тока. Токи в ветвях направляем произвольно и обозначаем их I 1; I 2; I.
необходимо найти 3 тока. Токи в ветвях направляем произвольно и обозначаем их I 1; I 2; I.
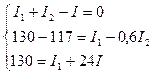




 В рассмотренной схеме источник Е 1 работает в режиме генератора ;
В рассмотренной схеме источник Е 1 работает в режиме генератора ;


 R0 1 +
R0 1 + 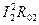 + I 2 R.
+ I 2 R.









 ○ ○
○ ○
 ○
○


 ○
○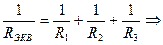
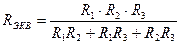

 I 1 I 2 I 3
I 1 I 2 I 3

 E R 2 R 3
E R 2 R 3

 R 0
R 4
R 0
R 4

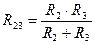





 I 1
I 1


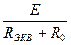 .
.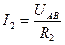






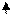








 A
A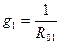 ;
; 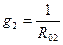 ;
; 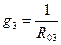 ;
; 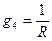
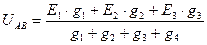
 R 3
R 3