Машины Тьюринга. Операции с машинами. Тезис Черча

Описание машины Тьюринга:

1. Конечная лента, разбитая на конечное число клеток(ячеек). В процессе работы машины к ленте могут пристраиваться новые ячейки. В каждой ячейке ленты записан один из конечного числа символов, составляющих внешний алфавит . Клетка, в которой записан символ  , обычно обозначаемый 0, называется пустой. Все вновь пристраиваемые клетки являются пустыми.

2. внутренняя память – некоторое устройство, которое в каждый момент находится в одном из конечного числа «состояний», составляющих внутренний алфавит Q={q₀,q₁,…,q_n}. Состояние q₀ называется заключительным.

3. Управляющая головка – некоторое устройство, которое может помещаться вдоль ленты так, что в каждый момент находится в определенной ячейке, или «обозревает» эту ячейку.

4. Механическое устройство, которое в зависимости от содержимого обозреваемой ячейки и состояния внутренней памяти может изменить состояние внутренней памяти и при этом либо изменить содержимое ячейки (обозреваемой), либо сдвинуть управляющую головку в соседнюю ячейку слева или в следующую ячейку справа.

Машинное слово машины Тьюринга (иначе – конфигурация):

a_j, a_j2,…, qa_jk…a_jz

Работа машины состоит в последовательном переходе от одной конфигурации к другой в результате выполнения команды.

Команды машины Тьюринга: q_ja_i→q_sa_r, q_ia_j→q_sR, q_ia_j→q_sL.

Совокупность команд называется программой.

Функции, вычислимые по Тьюрингу.

Композиция машин Тьюринга.

Тезис Черча: для любой вычислимой частичной функции существует машина Тьюринга, которая вычисляет эту функцию.

 

Конечные машины и бесконечные машины. Понятие программы

Эффективная нумерация программы. Теорема о параметризации. Существование универсальной программы.

Машина – абстрактное устройство, осуществляющее переработку информации. Другие названия – «абстрактная машина», «автомат».

Конечная машина представляет собой набор из пяти объектов {A, S, Z, ν, ξ}, где

А={a₀, a₁,…, a_n} – конечный список символов (входной, внешний алфавит)

Z={z₀, z₁,…,z_m} – список выходящих символов (выходной алфавит)

S={s₀, s₁,…, s_z} – множество внутренних состояний

ν: S×A→S – функция перехода (в следующее состояние)

ξ: S×A→Z – функция выхода (Биркгоф, Бари – современная прикладная алгебра)

Примеры конечных автоматов. Покрытие и эквивалентность. Машина Тьюринга, как конечная машина.

Бесконечные машины определяются аналогично конечным. В определении бесконечных машин алфавиты A, Z или S могут быть бесконечным.

Типы бесконечных машин.

Теорема параметризации. Существование универсальной программы. Теорема об универсальности.

 

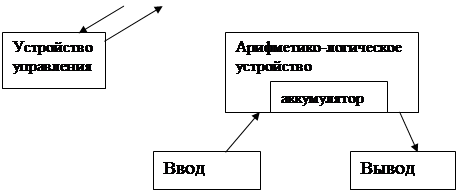
Компьютер фон Неймана

Архитектура Эккерта – фон Неймана и концепция хранимой программы. Историческая справка. Описание машины фон – Неймана.

Машина фон – Неймана представляет собой вычислительную систему, построенная на следующих принципах:

1. основными ее блоками является арифметико-логическое устройство, устройство управления, запоминающее устройство и устройство ввода-вывода.

2. Программы и данные хранятся в одной и той же памяти.

3. Устройство управления и арифметико-логическое устройство, обычно объединенные в центральный процессор, определяют действия, подлежащие выполнению путем считывания команд из оперативной памяти.

4. Внутренний код машины двоичен.

Подавляющее большинство вычислительных машин(компьютеров) в настоящее время является фон-неймановскими машинами. Свое название эта архитектура получила в честь американского ученого Джона фон Неймана (von Neumann). В литературе эта точка зрения воспринимается неоднозначно.

 

Архитектура машины фон – Неймана.

 

		Память