
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовые функции и алгоритмы их вычисления. Понятие вычислимой функцииСодержание книги
Поиск на нашем сайте
Вычислимая функция – функция, заданная на множестве натуральных чисел, всюду определенная и обладающая алгоритмом вычисления ее значений. Примеры числовых функций и алгоритмов их вычисления. 1. 2. f(x,y)={ наибольший общий делитель чисел x и y}. Алгоритмом, вычисляющим эту функцию служит алгоритм Евклида. 3. f(x,y)={натуральное число ≤9, чья цифровая запись является x-м десятичным знаком в десятичном разложении числа π}. В качестве алгоритма можно взять квадратуру круга, радиуса 1 по правилу Симпсона. 4. f(x,y)={сумма x и y}. Алгоритмом служит известное правило сложения натуральных чисел, записанных в десятичной системе счисления. 5. f(x,y)={произведение x и y}. Алгоритм умножения, изучают в школьном курсе математики.
Разрешимы и неразрешимые множества. График вычислимой функции Пусть А – подмножество множества натуральных чисел. Характеристической функцией множества А называется функция Определение: Множество А называется разрешимым, если его характеристическая функция ХА вычислима. Теорема 1. Если А и В – разрешимые множества, то множества Полухарактеристическая функция множества А:
Определение: множество А называется полуразрешимым, если его полухарактеристическая функция Теорема 2. Всякое разрешимое множество полуразрешимо. Теорема 3. (теорема Поста). Множество Определение: Множество Теорема 4. Всякое перечислимое множество полуразрешимо. Теорема 5. (теорема о графике). Частичная функция f из А в В вычислима тогда и только тогда, когда ее график Гf перечислим.
Формальная теория вычислимости. Исходные функции. Частично рекурсивные функции. Рекурсивные предикаты Простейшие функции: Основные вычислительные операторы: оператор суперпозиции частичных функций, оператор примитивной рекурсии. Примитивно рекурсивные функции. Примеры примитивно рекурсивных функций. Оператор минимизации. Частично рекурсивные функции. Общерекурсивные функции.
Рекурсивные предикаты. Пусть Р – n- местный предикат на множестве натуральных чисел N. Функция Определение: Предикат Р называется рекурсивным (примитивно рекурсивным) если его характеристические функция общерекурсивна(примитивно рекурсивна).
Логические операции над предикатами. Ограниченные кванторы. Постановка функции в предикат. Кусочное задание функции Над предикатами, заданными на множестве натуральных чисел N будем использовать операции отрицания (), конъюнкции(^), дизъюнкции(
Например, запись Теорема. Предикаты, которые можно получить из примитивно рекурсивных(или рекурсивных) с помощью логических операций и ограниченных кванторов также примитивно рекурсивны (соотв. рекурсивны). Подстановка функции в предикат используется при доказательстве примитивной рекурсивности функций, заданных кусочно. Определение: функция
При этом предполагается, что для каждого набора Теорема. Если функции
|
|||||
|
Последнее изменение этой страницы: 2021-04-20; просмотров: 114; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.5.176 (0.009 с.) |

 . В качестве алгоритма используется решение Эратосфена.
. В качестве алгоритма используется решение Эратосфена. определяемая условиями
определяемая условиями 
 разрешимы.
разрешимы. , такая что
, такая что 
 вычислима.
вычислима. разрешимо тогда и только тогда, когда оба множества А и N\A полуразрешимы.
разрешимо тогда и только тогда, когда оба множества А и N\A полуразрешимы. или А является множеством значений некоторой вычислимой функции.
или А является множеством значений некоторой вычислимой функции.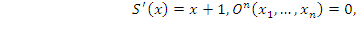
 называется характеристической для предиката Р, если эта функция удовлетворяет условиям
называется характеристической для предиката Р, если эта функция удовлетворяет условиям 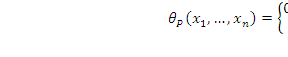
 , импликации(→) и эквивалентности, а также ограниченные кванторы:
, импликации(→) и эквивалентности, а также ограниченные кванторы: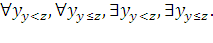
 означает предикаты «для любого у такого, что y<z и
означает предикаты «для любого у такого, что y<z и  ».
». называется кусочно заданной, если она удовлетворяет условиям:
называется кусочно заданной, если она удовлетворяет условиям: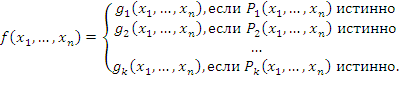
 значений переменных истинно одно и только одно из высказываний
значений переменных истинно одно и только одно из высказываний 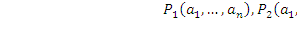 .
. и предикаты
и предикаты  примитивно рекурсивны (рекурсивны), то функция
примитивно рекурсивны (рекурсивны), то функция 


