
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Физические основы регистрации и дозиметрии ионизирующих излученийСодержание книги
Поиск на нашем сайте
Основа регистрации любого вида излучения – его взаимодействие с веществом детектора. Детектор при этом рассматривается как устройство, на вход которого поступают ионизирующие частицы и на выходе появляются сигналы. В зависимости от типа детектора сигналом могут быть вспышки света (сцинтилляционный детектор), импульсы тока (ионизационный детектор) и т.д. Неотъемлемая часть любого детектора – чувствительный объем, в котором энергия ионизирующего излучения в процессе взаимодействия с веществом преобразуется в определенный вид сигнала. Вещество, представляющее собой чувствительный объем, может быть газом, жидкостью, твердым телом; это и дает соответствующие названия детекторам: газовые, жидкостные, твердотельные. Для определения дозиметрических характеристик регистрируемого излучения необходимо установить связь между сигналом, сформированным детектором, и дозой (мощностью дозы) излучения. Ниже на примере фотонного излучения приведены наиболее важные понятия и определения, необходимые для установления этой связи. Электронное равновесие – состояние взаимодействия фотонов со средой, при котором поглощенная энергия излучения в заданном объеме среды равна суммарной кинетической энергии электронов, освобожденных фотонами в том же объеме. При электронном равновесии суммарная кинетическая энергия всех электронов, входящих в рассматриваемый объем, равна суммарной кинетической энергии электронов, покидающих его[20]. Соотношение Брэгга-Грея. Рассмотрим теперь ионизацию, возникающую под действием фотонного излучения в газовой полости, находящейся внутри твердого тела. Грей показал, что при выполнении ряда допущений введение в твердую среду малой газовой полости не искажает углового и энергетического распределения вторичных электронов в месте расположения полости. Указанные допущения заключаются в следующем: интенсивность первичного излучения одинакова в твердом теле и газовой полости; линейные размеры газовой полости должны быть намного меньше пробега в ней вторичных электронов. Поскольку ионизацию газа обусловливают электроны, освобожденные как в газовой полости, так и в твердом веществе, второе допущение означает, что лишь малая часть электронов будет заканчивать свой пробег в газовой полости, причем в пределах полости они потеряют пренебрежимо малую часть своей энергии. Следовательно, вкладом в полную ионизацию от электронов, освобожденных в газовой полости, можно пренебречь. Это означает, что энергетический спектр и поток электронов через поверхность, ограничивающую газовую полость, остаются такими же, как если бы вместо полости было твердое вещество.
Газовая полость (внутри твердого тела) для достижения в ней электронного равновесия должна быть окружена слоем твердого вещества, толщина которого больше максимального пробега вторичных электронов в твердом веществе. Это означает, что в любом элементарном объеме твердого вещества около полости поглощенная энергия излучения равна кинетической энергии вторичных электронов. Брэгг установил соотношение между ионизацией в газовой полости, облученной фотонами, и тормозной способностью окружающего газовую полость твердого вещества. Тормозная способность определяется как средняя потеря энергии на единице пути электронами, освобожденными фотонным излучением. Принцип Брэгга-Грея гласит, что отношение энергии, поглощенной в единицу времени в единице объема твердого вещества вблизи газовой полости Δ ЕZ, к аналогичной величине в газе (например, воздухе) Δ Е В равно отношению электронных тормозных способностей твердого вещества SZ и газа S В:
Поскольку поглощенная энергия в воздухе равна
где n – число пар ионов, образующихся в единицу времени в единице объема полости, w – средняя энергия ионообразования в газе, то
где Формула (8.3) носит название формулы Брэгга-Грея, она устанавливает связь между поглощенной энергией в полости и окружающей ее стенке. Измерив n и зная w и отношение тормозных способностей k, можно определить поглощенную дозу в любом твердом веществе, окружающем газовую полость. В общем случае формула Брэгга-Грея справедлива при выполнении указанных выше допущений. В частном случае, при одинаковом атомном составе газовой полости и окружающей твердой стенки формула справедлива для полости любых размеров[21].
Эффективный атомный номер вещества. Под эффективным атомным номером сложного вещества понимается атомный номер такого условного простого вещества, для которого коэффициент передачи энергии излучения, рассчитанный на один электрон среды, является таким же, как и для данного сложного вещества. Если выполняются условия электронного равновесия, энергия фотонного излучения, преобразованная в данном веществе в кинетическую энергию заряженных частиц, равна поглощенной энергии излучения. Следовательно, для любых веществ с одинаковым атомным номером при обеспечении электронного равновесия и в тождественных условиях облучения поглощенная энергия излучения, приходящаяся на один электрон облучаемой среды, будет одинаковой. Как мы знаем, линейный коэффициент ослабления γ-квантов μ может быть массовым (μ m), атомным (μ a) и электронным (μ e). Связь между этими коэффициентами определяется соотношениями[22]
где ρ – плотность вещества; ne, n а – число электронов и атомов в единице массы вещества соответственно. Из формулы (8.4) видно, что электронный коэффициент ослабления μ е (рассчитанный на один электрон среды) связан с массовым коэффициентом ослабления μ m (рассчитанным на единицу массы среды) соотношением
где ne – число электронов в единице массы вещества. К массовым коэффициентам ослабления применимо правило аддитивности
где р i – массовая доля i -го простого вещества, входящего в состав сложного вещества; μ mi – массовый коэффициент ослаб-ления в i -м простом веществе; μ m – массовый коэффициент ослабления для сложного вещества. Массовый μ mi и электронный μ е i коэффициенты ослабления связаны соотношением
где величина
Если принять, что отношение Z / M для большинства элементов примерно постоянно, можно трактовать величину Если для расчетов необходимо использовать число атомов элементов, входящих в состав сложного вещества, то очевидно, что относительное число атомов а i и относительное число электронов α i связаны соотношением[23]
Тогда, подставив (8.9) в (8.8), получим выражение для атомного коэффициента ослабления в сложном веществе
Если в каком-либо веществе одновременно идут все три процесса взаимодействия гамма-квантов (фотоэффект, эффект Комптона, эффект образования пар), то электронный коэффициент передачи энергии, а в случае выполнения условий электронного равновесия и коэффициент поглощения энергии в i -м простом веществе будет равен сумме трех коэффициентов:
Сечение фотоэффекта как функция энергии гамма-кванта и атомного номера среды описывается зависимостью
Достаточно трудно определить эффективный атомный номер сложного вещества при одновременно идущих всех трех процессах. Однако на практике фотоэффект и образование пар редко идут вместе (см. табл. 2.1), поэтому Zэфф определяют для всех трех процессов отдельно. Так, для фотоэффекта
здесь n – слабо зависящий от энергии фотонов коэффициент часто принимается равным трем. В правой части написано выражение для коэффициента передачи (поглощения) энергии в таком простом веществе, в котором рассчитанная энергия на один электрон фотонного излучения, преобразованная в энергию заряженных частиц, такая же, как в сложном веществе. Атомный номер такого простого вещества и есть эффективный атомный номер Z эфф сложного вещества:
Для n = 3 получаются следующие формулы для расчета Z эфф сложного вещества по фотоэффекту:
где
Для некогерентного рассеяния (эффекта Комптона) коэффициент передачи энергии, рассчитанный на один электрон, не зависит от Z вещества, поэтому определение Z эфф в этом случае не имеет смысла. Для эффекта образования пар
или
Следовательно, при одновременно происходящих фотоэффекте и эффекте Комптона Z эфф следует вычислять по формулам (8.15) и (8.16), а при одновременно происходящих эффектах Комптона и образования пар Z эфф вычисляют по формулам (8.17) и (8.18).
|
|||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-20; просмотров: 107; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.241.205 (0.01 с.) |

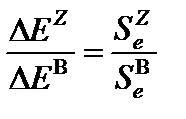 .
.
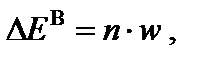
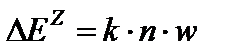 ,
,
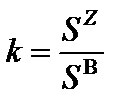 – среднее значение отношения электронных тормоз-ных способностей твердого вещества и газа.
– среднее значение отношения электронных тормоз-ных способностей твердого вещества и газа.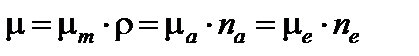 ,
,
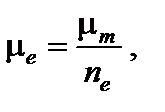
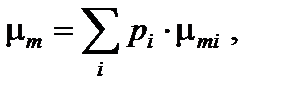
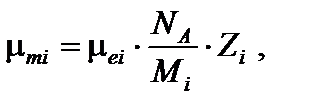
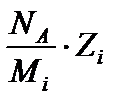 равна числу электронов в единице массы вещества. Здесь N А – число Авогадро; Zi, Mi – зарядовое и массовое числа соответственно. Теперь можно записать формулу (8.5) в следующем виде:
равна числу электронов в единице массы вещества. Здесь N А – число Авогадро; Zi, Mi – зарядовое и массовое числа соответственно. Теперь можно записать формулу (8.5) в следующем виде: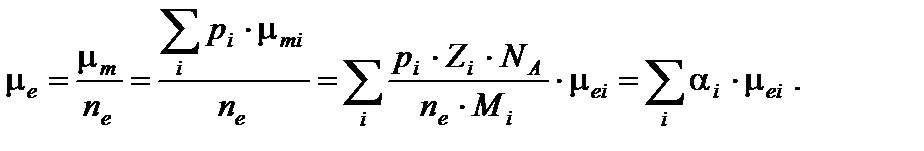
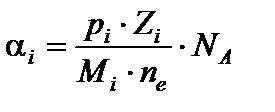 как относительное число электронов простого элемента по отношению к общему числу электронов, находящихся в рассматриваемом объеме.
как относительное число электронов простого элемента по отношению к общему числу электронов, находящихся в рассматриваемом объеме.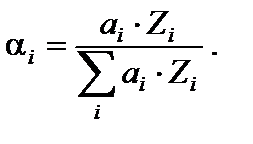
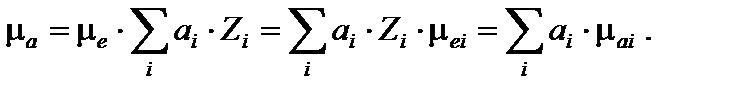
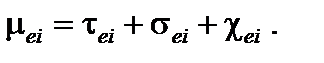
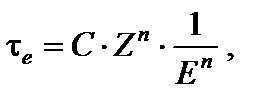 сечение комптоновского рассеяния σ е ~ σ е и сечение образования пар χ e ≈ k · Z, т.е. для сложного вещества можно записать
сечение комптоновского рассеяния σ е ~ σ е и сечение образования пар χ e ≈ k · Z, т.е. для сложного вещества можно записать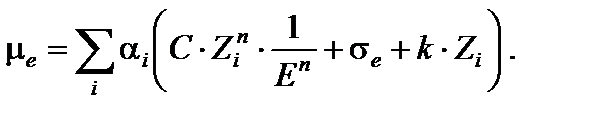
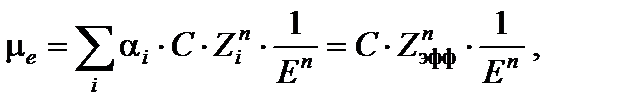
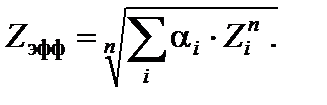

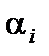 – относительная концентрация электронов i -го элемента. Если используется относительная концентрация атомов а i, то
– относительная концентрация электронов i -го элемента. Если используется относительная концентрация атомов а i, то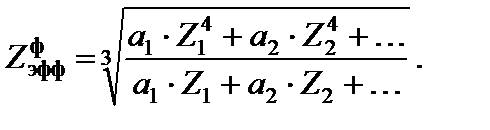
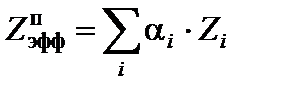
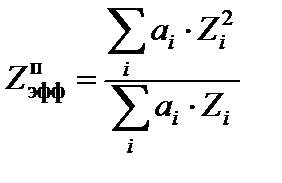 .
.



