
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема. Вероятность появления хотя бы одного события.Содержание книги
Поиск на нашем сайте
ЛЕКЦИЯ 2 (продолжение) Теорема. Вероятность появления хотя бы одного события. Вероятность появления хотя бы одного из событий A1, A2,… An находится по формуле: P (A1 + A2 +…+ An) = 1 - P Доказательство Пусть событие A заключается в появлении хотя бы одного из событий A1, A2,… An . Тогда A = A1 + A2 +…+ An. Рассмотрим противоположное событие событий A1, A2,… An. Тогда P(A) = 1 – P(
Определение. Надежностью элемента называется вероятность его безотказной работы в течение определенного промежутка времени.
Пример. Определить надежность схемы, если надежности элементов А 0,6; 0,4;0,5; 0,3 и 0,9.
Решение. Пусть событие А – схема работает. Тогда А = А Поэтому Р(А) = Р(А по теореме умножения независимых событий = Р(А по теореме о вероятности появления хотя бы одного события = Р(А по теореме умножения независимых событий = Р(А Статистическое определение вероятности На основании опыта мы считаем более вероятными те события, которые происходят чаще, менее вероятными – которые происходят реже. Таким образом, понятие вероятности события в самой своей основе связано с практическим понятием частоты события. Определение. Частотой события А в данной серии опытов называется отношение числа опытов, в которых появилось событие А, к общему числу произведенных опытов: Pn Частоту события часто называют его статистической вероятностью. При небольшом количестве опытов частота события носит в значительной мере случайный характер и может заметно меняться от одной группы опытов к другой. Однако при увеличении числа опытов частота события все более теряет свой случайный характер, проявляет тенденцию стабилизироваться. Пример. Опыт Бюффона. Французский естествоиспытатель Жорж-Луи Бюффон (1707 – 1788) бросил монету 4040 раз, герб выпал 2048 раз. Частота появления герба
Теорема. Проводится n независимых опытов, в каждом из которых может произойти или не произойти некоторое событие А. Вероятность появления события А (успех испытания) в каждом опыте Р(А) = р. Вероятность непоявления события А (неуспех испытания) в каждом опыте Р(Ā) = q = 1 - р. Тогда вероятность того, что при n испытаниях Бернулли будет k «успехов» находится по формуле Бернулли: Рn(k) = Доказательство.
Рассмотрим событие Вk, состоящее в том, что событие А появится при n испытаниях ровно kраз. Будем обозначать через Аiпоявление, а через Āi - не появление события А в i-ом эксперименте, Р(Аi) = р, Р(Āi) = q. События А1, А2 , …,Аn независимы. Каждый способ реализации события Вk (т.е. каждый член суммы разложения события Вk) должен состоять из k появлений события А и n – k не появлений, т.е. Вk = А1А2 … Аk Āk+1 … Ān + … + Ā1 Ā2 … Ān-k Аn-k+1 … Аn, При этом в каждое такое произведение событие Аi должно входить k раз, а событие Āj - n – k раз. Число всех комбинаций такого рода равно числу способов Рn(k) = Следствие. Вероятность того, что событие А появится не менее m 1 и не более m 2 раз при n испытаниях Бернулли определяется по формуле
Локальная теорема Муавра – Лапласа
Формула Бернулли Рn(k) = Теорема (локальная теорема Муавра-Лапласа). Если вероятность p наступления события A в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что событие A произойдёт k раз в n независимых испытаниях при достаточно больших значениях n, приближённо равна
Рn(k) = где
(без доказательства). Локальную теорему Муавра-Лапласа применяют, если выполнено условие n × p × q ³ 20. Значения функции j (x) можно вычислить на калькуляторе или найти с помощью таблицы, приведенной в Приложении 1 (Гмурман). При этом следует иметь в виду, что j (x) чётная функция, значит, j (- x) = j (x). Можно также считать, что, если x > 4, то j (x) = 0. Пример. Вычислить вероятность того, что при 100-кратном бросании монеты орёл выпадет ровно 60 раз. Решение. Имеем n = 100; p = 0,5; q = 0,5. Условие n × p × q = 100×0,5×0,5 = 25 ³ 20 выполнено. Применим формулу Муавра-Лапласа
Р100(60)≈ Ответ: 0,0108.
Интегральная теорема Муавра-Лапласа Теорема. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события A постоянна и равна p (0 < p < 1) событие A наступит не менее m 1 и не более m 2 раз приближённо равна P (m 1, m 2) = F(x 2) - F(x 1).
Здесь F(x) =
x 1 = (m 1 – np)/
Таблица значений функции Лапласа F(x) для положительных значений x (0 ≤ x ≤ 5) приведена в Приложении 2 (Гмурман). При этом следует иметь в виду, что F(x) нечётная функция, поэтому F(- x) = - F(x). Можно также считать, что, если x > 5, то F(x) = 0,5. Пример. Вычислить вероятность того, что при 100-кратном бросании монеты орёл выпадет не менее 40 и не более 60 раз. Решение. Имеем n = 100; p = 0,5; q = 0,5; m 1 = 40; m 2 = 60. Применим интегральную формулу Муавра-Лапласа
P (40, 60) = F(x 2) - F(x 1),
где F(x) - функция Лапласа, x 1 = (40 - 100×0,5)/
x 2 = (60 - 100×0,5)/
Учитывая, что функция Лапласа нечётная функция, получим
P (40 ≤ m ≤ 60) = F (2) - F (-2) = 2 F (2).
По таблице Приложения 2 (Гмурман) находим F (2) = 0,4772. Значит, P (40 ≤ m ≤ 60) = 2×0,4772 = 0,9545.
Ответ: 0,9545.
Формула Пуассона
Если вероятность p наступления события A в каждом испытании есть малое число, а число испытаний n - велико, то формула Бернулли становится громоздкой и непригодна для вычислений. В этом случае вычисления выполняют по приближенной формуле Пуассона. Теорема. Если вероятность p наступления события A в каждом испытании стремится к нулю (p ®0) при неограниченном увеличении числа n испытаний (n ®¥), причём произведение np стремится к постоянному числу l (np ® l), то вероятность Рn(k) =
Рn(k) где l = n × p.
Эта формула называется формулой Пуассона
Пример: На факультете насчитывается 1606 студентов. Какова вероятность того, что 23 апреля является днём рождения одновременно 5 студентов? Решение: Применим формулу Пуассона потому, что вероятность p = 1/365 - мала, а число n = 1606 - велико. Вычислим l = np; l = 1606/365 =4,4. Положим в формуле Пуассона k = 5, l = 4,4; в результате получим
Р1606(5)
Ответ: 0,169. ЛЕКЦИЯ № 3 ЛЕКЦИЯ 2 (продолжение) Теорема. Вероятность появления хотя бы одного события. Вероятность появления хотя бы одного из событий A1, A2,… An находится по формуле: P (A1 + A2 +…+ An) = 1 - P Доказательство Пусть событие A заключается в появлении хотя бы одного из событий A1, A2,… An . Тогда A = A1 + A2 +…+ An. Рассмотрим противоположное событие событий A1, A2,… An. Тогда P(A) = 1 – P(
Определение. Надежностью элемента называется вероятность его безотказной работы в течение определенного промежутка времени.
Пример. Определить надежность схемы, если надежности элементов А 0,6; 0,4;0,5; 0,3 и 0,9.
Решение. Пусть событие А – схема работает. Тогда А = А Поэтому Р(А) = Р(А по теореме умножения независимых событий = Р(А по теореме о вероятности появления хотя бы одного события = Р(А по теореме умножения независимых событий = Р(А
|
||||
|
Последнее изменение этой страницы: 2021-04-14; просмотров: 150; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |


 - не произошло ни одно из
- не произошло ни одно из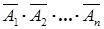 . Следовательно,
. Следовательно,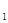 , А
, А 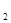 , А
, А 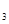 , А
, А 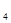 и А
и А 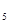 , работающих независимо, соответственно равна
, работающих независимо, соответственно равна
 )·Р(А
)·Р(А  )·Р(А
)·Р(А 

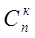 рk qn-k.
рk qn-k.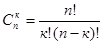 выбора k экспериментов, в которых осуществлялось событие А, из n экспериментов. Вероятность каждой такой комбинации по теореме умножения для независимых событий, равна рkqn-k. Так как эти комбинации между собой несовместны, то по теореме сложения вероятность события Вk равна
выбора k экспериментов, в которых осуществлялось событие А, из n экспериментов. Вероятность каждой такой комбинации по теореме умножения для независимых событий, равна рkqn-k. Так как эти комбинации между собой несовместны, то по теореме сложения вероятность события Вk равна 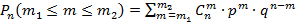 .
. ,
,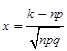 ;
; 
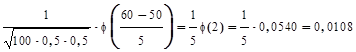
 - функция Лапласа,
- функция Лапласа,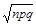 , x 2 = (m 2 – np)/
, x 2 = (m 2 – np)/ 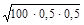 = -2,
= -2,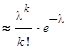 ,
,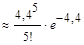 =
= 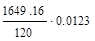 = 0,169.
= 0,169.


