Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы корреляционного и регрессионного анализа . Задачи типа 6
Связи между различными явлениями в природе сложны и многообразны, их можно определенным образом классифицировать. В технике и естествознании часто речь идет о функциональной зависимости между переменными х и у, когда каждому возможному значению х поставлено в однозначное соответствие определенное значение у, например, зависимость между давлением и объемом газа (закон Бойля-Мариотта). В реальном мире многие явления природы происходят в обстановке действия многочисленных факторов, влияние каждого из которых мало, а число их велико. В этом случае связь теряет свою однозначность и изучаемая физическая система переходит не в определенное состояние, а в одно из возможных для нее состояний. Зависимость между величинами Х и У называется статистической, если каждому значению одной переменной соответствует несколько значений другой, встречающихся не одинаково часто. Иными словами, каждому значению одной величины Х соответствует закон распределения другой величины У. Статистическая зависимость между величинами Х и У называется корреляционной, если изменение величины Х влечет за собой изменение среднего значения величины У. Пример. Изучается зависимость между величинами Х и У. Каждому значению Х соответствует несколько значений У.
Условной средней
Заметим, что каждому значению величины Х соответствует единственное значение условной средней, т.е. зависимость является функциональной: Следовательно, корреляционной зависимостью между величинами Х и У называется функциональная зависимость условной средней График функции В корреляционном анализе решают две основные задачи: 1) Установить форму корреляционной связи, т.е. установить вид функций f(x), φ(y) (линейные, квадратические, показательные и др.). Для определения вида зависимости в прямоугольной системе координат строят точки, координаты которых (х, у) получены в результате наблюдений. Если точки расположены, например, вблизи некоторой прямой, то корреляцию называют линейной.
2) Оценить тесноту корреляционной связи степенью рассеивания значений у около условной средней Большое рассеивание свидетельствует о слабой зависимости у от х или об ее отсутствии. Малое рассеивание свидетельствует о наличии тесной связи между х и у. Пусть установлено, что зависимость между признаками Х и У имеет линейный характер. Тогда уравнение регрессии может быть представлено в виде:
При этом х называется регрессором, угловой коэффициент прямой а 0 называется коэффициентом регрессии у на х и обозначается
Если r > 0, то увеличение одной величины ведет к увеличению другой величины; если r < 0, то увеличение одной величины ведет к уменьшению другой. Если r = 0, то рассматриваемые признаки не связаны линейной зависимостью. Чем больше
Уравнение регрессии будем искать в виде: y = a 0 x + a 1. Параметры этого уравнения a 0 и a 1 определим методом наименьших квадратов. Суть метода состоит в следующем. Предположим, что у =f(x) – искомая формула зависимости. Разности f(x i) – y i = εi, i = 1, 2,…, n, назовем отклонениями. Параметры формулы у =f(x) подбирают так, чтобы сумма квадратов отклонений была наименьшей. В рассматриваемой задаче искомая формула f(x)= a 0 x + a 1. Тогда отклонение εi= a 0xi+ a 1–yi. Согласно методу наименьших квадратов подберем a 0 и a 1 так, чтобы сумма
Необходимые условия экстремума функции двух переменных: Или Преобразуем систему уравнений к виду:
Система называется нормальной системой метода наименьших квадратов. Решить ее можно, например, по правилу Крамера. Тогда Коэффициент корреляции r определим по формуле:
Ошибку коэффициента корреляции найдем по формуле Пример. Результаты измерений величин Х и У представлены таблицей:
1) Построить в прямоугольной системе координат заданные точки; убедиться, что величины Х и У связаны линейной зависимостью. 2) Составить уравнение регрессии у(х). Построить полученную прямую. 3) Вычислить коэффициент корреляции r и его ошибку Sr; оценить тесноту связи между Х и У. Решение. Составим расчетную таблицу:
Составим нормальную систему уравнений:
Решим ее по правилу Крамера:
Отсюда Искомое уравнение регрессии у = 1,873 х – 13,165. Для построения полученной прямой найдем две точки:
Коэффициент корреляции найдем по формуле:
Построим точки (x i, y i) и прямую линии регрессии.
Рисунок 5.1 – Прямая линия регрессии
Вопросы для самоконтроля. 1. Какие значения может принимать коэффициент корреляции? 2. Как определяется значимость коэффициента корреляции? 3. Что называется регрессией у на х? 4. Как задается парная линейная регрессия? 5. Какой метод используется для вычисления коэффициентов парной линейной регрессии? 6. Как определяются коэффициенты парной линейной регрессии? Рекомендуемая литература: [1, c.182-186, 253-264], [2, c.190-196].
ВОПРОСЫ ДЛЯ ПОДГОТОВКИ КСЕМЕСТРОВОМУ КОНТРОЛЮ
1. Предмет теории вероятностей. Событие. Классификация событий. 2. Классическое и статистическое определение вероятности. Свойства вероятности. 3. Элементы комбинаторики. 4. Зависимые и независимые события. Произведение событий. 5. Теоремы умножения вероятностей. 6. Независимые события. Теорема умножения для независимых событий. 7. Условная вероятность. Теорема умножения вероятностей зависимых событий. 8. Сумма событий. Совместные и несовместные события. Теоремы сложения вероятностей. 9. Полная группа событий. Сумма вероятностей событий, образующих полную группу. 10. Вероятность противоположного события; вероятность осуществления только одного события; вероятность осуществления хотя бы одного события. 11. Формула полной вероятности. 12. Вероятность гипотез. Формула Бейеса. 13. Формула Бернулли. 14. Локальная и интегральная теоремы Муавра-Лапласа. 15. Формула Пуассона для редких событий. 16. Наивероятнейшее число появления события в серии повторяющихся испытаний. 17. Дискретные и непрерывные случайные величины.
18. Закон распределения вероятностей случайной величины. 19. Математическое ожидание дискретной случайной величины. Свойства математического ожидания. 20. Вероятностный смысл математического ожидания. 21. Дисперсия, среднеквадратическое отклонение, мода дискретной случайной величины. 22. Свойства дисперсии дискретной случайной величины. 23. Определение функции распределения и ее свойства. 24. График функции распределения дискретной случайной величины. 25. Плотность распределения вероятностей непрерывной случайной величины. 26. Свойства функции плотности распределения вероятностей непрерывной случайной величины. 27. Математическое ожидание непрерывной случайной величины. 28. Дисперсия и среднеквадратическое отклонение непрерывной случайной величины. 29. Моменты случайной величины. 30. Асимметрия, эксцесс, мода, медиана случайной величины. 31. Биномиальное распределение. 32. Распределение Пуассона. 33. Равномерный закон распределения. 34. Показательный закон распределения. 35. Нормальный закон распределения. Основные параметры. Вероятностный смысл параметров. 36. Вероятность попадания нормально распределенной непрерывной случайной величины в заданный интервал. 37. Правило «трех» сигм. 38. Теорема Бернулли. 39. Формулировка центральной предельной теоремы (теорема Ляпунова). 40. Математическая статистика, основные задачи. Понятие первичной статистической совокупности. 41. Интервальные и безинтервальные вариационные ряды. Графическое изображение вариационных рядов: полигон, гистограмма, кумулята, эмпирическая функция распределения. 42. Элементы корреляционного анализа. Линейная корреляция. Уравнения прямых линий регрессии. 43. Коэффициент корреляции. Оценка коэффициента корреляции по выборочным данным. 44. Определение параметров уравнения регрессии методом наименьших квадратов. 45. Критерии согласия. Статистические гипотезы. 46. Критерий согласия Пирсона.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-13; просмотров: 102; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.167.176 (0.043 с.) |
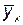 называется среднее арифметическое значений У, соответствующих данному значению Х. Так
называется среднее арифметическое значений У, соответствующих данному значению Х. Так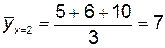 ;
; 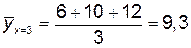 ;
; 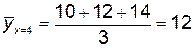 .
.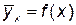 .
.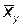 , определить зависимость
, определить зависимость 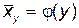 и построить линию регрессии х на у.
и построить линию регрессии х на у. .
. . Если исследуемая зависимость представлена в виде
. Если исследуемая зависимость представлена в виде 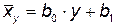 , то коэффициент b 0 называется коэффициентом регрессии х на у и обозначается
, то коэффициент b 0 называется коэффициентом регрессии х на у и обозначается  . В качестве меры тесноты связи в случае линейной зависимости используют коэффициент корреляции r:
. В качестве меры тесноты связи в случае линейной зависимости используют коэффициент корреляции r: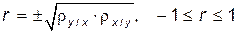 .
.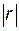 , тем теснее линейная связь между Х и У, и при
, тем теснее линейная связь между Х и У, и при  переходит в функциональную. При
переходит в функциональную. При  - связь слабая, при
- связь слабая, при  - средняя, при
- средняя, при 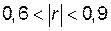 - сильная, при
- сильная, при  - значительная, почти функциональная. Коэффициент корреляции r, как и другой выборочный показатель, служит оценкой для генерального истинного коэффициента корреляции, его ошибка при п < 100
- значительная, почти функциональная. Коэффициент корреляции r, как и другой выборочный показатель, служит оценкой для генерального истинного коэффициента корреляции, его ошибка при п < 100 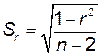 . Пусть в результате наблюдений получены значения величин Х и У:
. Пусть в результате наблюдений получены значения величин Х и У: была наименьшей. При любых значениях a 0, a 1 функция
была наименьшей. При любых значениях a 0, a 1 функция  , следовательно, если она имеет экстремум, то это будет минимум.
, следовательно, если она имеет экстремум, то это будет минимум.
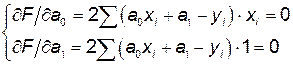
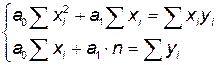
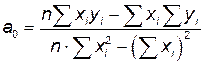 ,
,  , при этом коэффициент а 0 =
, при этом коэффициент а 0 =  .
. .
.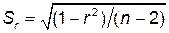 .
.
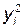
 : 137
: 137
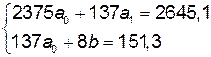
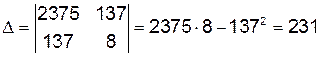 ,
, ,
,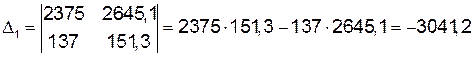 .
. ,
, 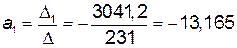 .
.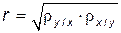 , где
, где 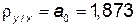 ,
, ,
, . Следовательно, связь между Х и У сильная, почти функциональная. Ошибка коэффициента корреляции:
. Следовательно, связь между Х и У сильная, почти функциональная. Ошибка коэффициента корреляции: