Вопрос 5. Анализ пространственных данных

 

Задачи пространственного анализа

К средствам пространственного анализа относятся различные процедуры манипулирования пространственными и атрибутивными данными, выполняемые при обработке запросов пользователя. К ним относятся, например, операции наложения графических объектов, средства анализа сетевых структур или выделения объектов по заданным признакам.

Для каждого ГИС-пакета характерен свой набор средств пространственного анализа, обеспечивающий решение специфических задач пользователя, в тоже время можно выделить ряд основных функций, свойственных практически каждому ГИС-пакету. Это, прежде всего, организация выбора и объединения объектов в соответствии с заданными условиями, реализация операций вычислительной геометрии, анализ наложений, построение буферных зон, сетевой анализ.

Основные функции пространственного анализа данных

Выбор объектов по запросу: самой простой формой запроса является получение характеристик объекта указанного курсором на экране и обратная операция, когда изображаются объекты с заданными атрибутами. Более сложные запросы позволяют выбирать объекты по нескольким признакам, например по признаку удаленности одних объектов от других, совпадающие объекты, но расположенные в разных слоях и т. д.

Для выбора данных в соответствии с определенными условиями используются SQL- запросы. Для выполнения запросов разной сложности реализованы возможности использования при составлении запросов математических и статистических функций, а также географических операторов, позволяющих выбирать объекты на основании их взаимного расположения в пространстве (например, находится ли анализируемый объект внутри другого объекта или пересекается с ним).

Обобщение данных может проводиться по равенству значений определенного атрибута, в частности для зонирования территории. Еще один способ группировки – объединение объектов одного тематического слоя в соответствии с их размещением внутри полигональных объектов других тематических слоев.

Геометрические функции: к ним относят расчеты геометрических характеристик объектов или их взаимного положения в пространстве, при этом используются формулы аналитической геометрии на плоскости и в пространстве. Так для площадных объектов вычисляются занимаемые ими площади или периметры границ, для линейных - длины, а также расстояния между объектами и т.д.

Оверлейные операции (топологическое наложение слоев) являются одними из самых распространенных и эффективных средств. В результате наложения двух тематических слоев образуется другой дополнительный слой в виде графической композиции исходных слоев. Учитывая, что анализируемые объекты могут относиться к разным типам (точка, линия, полигон), возможны разные формы анализа: точка на точку, точка на полигон и т.д. Наиболее часто анализируется совмещение полигонов.

Построение буферных зон. Одним из средств анализа близости объектов является построение буферных зон. Буферные зоны – это районы (полигоны), граница которых отстоит на заданном расстоянии от границы исходного объекта. Границы таких зон вычисляются на основе анализа соответствующих атрибутивных характеристик. При этом ширина буферной зоны может быть как постоянной, так и переменной. Например, буферная зона вокруг источника электромагнитного излучения, будет иметь форму круга, а зона загрязнения от дымовой трубы завода с учетом розы ветров будет иметь форму близкую к эллипсу.

Сетевой анализ позволяет пользователю проанализировать пространственные сети связных линейных объектов (дороги, линии электропередач и т. д.). Обычно сетевой анализ служит для задач определения ближайшего, наиболее выгодного пути, определения уровня нагрузки на сеть, определение адреса объекта или маршрута по заданному адресу и другие задачи.

Анализ пространственного распределения объектов

Анализ пространственного распределения объектов. Фактически во многих случаях необходимо знать не только объем пространства, занимаемый объектами, но и расположение объектов в пространстве, которое может характеризоваться количеством объектов в определенной области, например, распределение численности населения. Наиболее распространены методы анализа распределения точечных объектов. Мерой точечного распределения служит плотность. Она определяется как результат деления числа точек на значение площади территории, на которой они расположены. Кроме плотности распределения можно оценить форму распределения. Точечные распределения встречаются в одном из четырёх возможных вариантов: равномерном (если число точек в каждой малой подобласти такое же, как и в любой другой подобласти), регулярном (если точки, разделённые одинаковыми интервалами по всей области, расположены в узлах сетки), случайном, кластерном (если точки собраны в тесные группы).

Точечные распределения могут описываться не только количеством точек в пределах подобластей. Часто анализируются локальные отношения внутри пар точек. Вычисление этого статистического показателя включает определение среднего расстояния до ближайшей соседней точки среди всех возможных пар ближайших точек. Данный метод позволяет оценить меру разреженности точек в распределении.

Распределение линий также оценивается по плотности. Обычно вычисления выполняются для сравнения разных географических областей, например по густоте гидрографической сети. Линии могут также оцениваться по близости и возможным пересечениям. Другими важными характеристиками являются ориентация, направленность и связанность.

Анализ распределения полигонов подобен анализу распределения точек, однако при оценке плотности определяют не количество полигонов на единицу площади, а относительную долю площади, занимаемой полигоном

 

Вопрос 6. МОДЕЛИРОВАНИЕ ПОВЕРХНОСТЕЙ

 

Поверхность и цифровая модель

 

Основой для представления данных о земной поверхности являются цифровые модели рельефа.

Поверхности – это объекты, которые чаще всего представляются значениями высоты Z, распределенными по области, определенной координатами X и Y.

Цифровые модели рельефа (ЦМР) используют для компьютерного представления земных поверхностей.

ЦМР – средство цифрового представления рельефа земной поверхности.

Построение ЦМР требует определённой формы представления исходных данных (набора координат точек X,Y,Z) и способа их структурного описания, позволяющего восстанавливать поверхность путем интерполяции или аппроксимации исходных данных.

Источники данных для формирования ЦМР

Исходные данные для формирования ЦМР могут быть получены по картам – цифрованием горизонталей, по стереопарам снимков, а также в результате геодезических измерений или лазерного сканирования местности. Наиболее распространен первый способ, т.к. сбор по стереопарам снимков отличается трудоемкостью и требует специфического программного обеспечения, но в то же время позволяет обеспечить желаемую степень детальности представления земной поверхности. Лазерное сканирование перспективный современный метод, пока достаточно дорогой.

Построение ЦМР требует определенной структуры данных, а исходные точки могут быть по разному распределены в пространстве. Сбор данных может осуществляться по точкам регулярной сетки, по структурным линиям рельефа или хаотично. Первичные данные с помощью тех или иных операций приводят к одному из наиболее распространенных в ГИС структур для представления поверхностей: GRID, TIN или TGRID.

TIN (Triangulated Irregular Network) – нерегулярная триангуляционная сеть, система неперекрывающихся треугольников. Вершинами треугольников являются исходные опорные точки. Рельеф в этом случае представляется многогранной поверхностью, каждая грань которой описывается либо линейной функцией (полиэдральная модель), либо полиноминальной поверхностью, коэффициенты которой определяются по значениям в вершинах граней треугольников. Для получения модели поверхности нужно соединить пары точек ребрами определенным способом, называемым триангуляцией Делоне (рис. 5).

Рис. 5. TIN модель

 

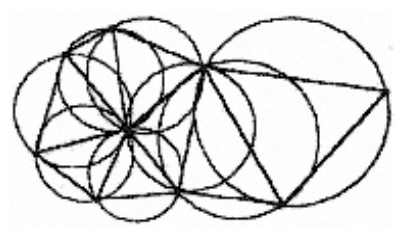
Триангуляция Делоне в приложении к двумерному пространству формулируется следующим образом: система взаимосвязанных неперекрывающихся треугольников имеет наименьший периметр, если ни одна из вершин не попадает внутрь ни одной из окружностей, описанных вокруг образованных треугольников (рис.6).

Образовавшиеся треугольники при такой триангуляции максимально приближаются к равносторонним, а каждая из сторон образовавшихся треугольников из противолежащей вершины видна под максимальным углом из всех возможных точек соответствующей полуплоскости. Интерполяция выполняется по образованным ребрам.

Рис. 6. Триангуляция Делоне

 

Отличительной особенностью и преимуществом триангуляционной модели является то, что в ней нет преобразований исходных данных. С одной стороны, это не дает использовать такие модели для детального анализа, но с другой стороны, исследователь всегда знает, что в этой модели нет привнесенных ошибок, которыми грешат модели, полученные при использовании других методов интерполяции. Немаловажен и тот факт, что это самый быстрый метод интерполяции. Однако, если в ранних версиях большинства ГИС триангуляционный методы был основной, то сегодня большое распространение получили модели в виде регулярной матрицы значений высот.

GRID – модель, представляет собой регулярную матрицу значений высот, полученную при интерполяции исходных данных. Для каждой ячейки матрицы высота вычисляется на основе интерполяции. Фактически это сетка, размеры которой задаются в соответствии с требованиями точности конкретной решаемой задачи. Регулярная сетка соответствует земной поверхности, а не изображению.

При использовании GRID-модели существует некоторая сложность в выборе интервала между точками. Например, участки поверхности могут быть как сильно пересеченными, так и выположенными. В первом случае необходимо большее количество точек на единицу площади.

Рис. 7. Плотность точек в модели GRID

 

TGRID (triangulated grid) – модель, сочетающая в себе элементы моделей TIN и GRID. Такие модели имеют свои преимущества, например, позволяют использовать дополнительные данные для описания сложных форм рельефа (обрывы, скальные выступы).

Интерполяции

Восстановление поверхностей реализуется на основе интерполяции исходных данных.

Интерполяция – восстановление функции на заданном интервале по известным ее значениям конечного множества точек, принадлежащих этому интервалу.

В настоящее время известны десятки методов интерполяции поверхностей, наиболее распространенные: линейная интерполяция; метод обратных взвешенных расстояний, кригинг; сплайн-интерполяция; тренд-интерполяция.

Кригинг. Метод интерполяции, который основан на использовании методов математической статистики. В его реализации применяется идея регионализированной переменной, т.е. переменной, которая изменяется от места к месту с некоторой видимой непрерывностью, поэтому не может моделироваться только одним математическим уравнением. Поверхность рассматривается в виде трех независимых величин. Первая - тренд, характеризует изменение поверхности в определенном направлении. Далее предполагается, что имеются небольшие отклонения от общей тенденции, вроде маленьких пиков и впадин, которые являются случайными, но все же связанными друг с другом пространственно.

Наконец, имеется случайный шум (например, валуны). С каждой из трех переменных надо оперировать в отдельности. Тренд оценивается с использованием математического уравнения, которое наиболее близко представляет общее изменение поверхности, во многом подобно поверхности тренда.

Рис. 8. Элементы кригинга: 1 - тренд, 2 - случайные, но пространственно связанные высотные колебания, 3 - случайный шум.

 

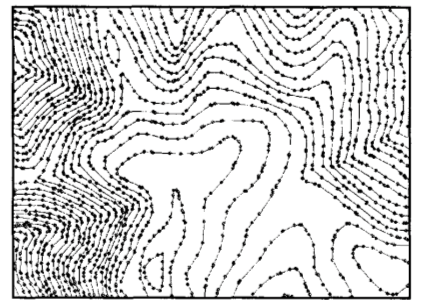
Ожидаемое изменение высоты измеряется по вариограмме, на которой по горизонтальной оси откладывается расстояние между отсчетами, а на вертикальной - полудисперсия. Полудисперсия определяется как половина дисперсии между значениями высоты исходных точек и высот соседних точек. Затем через точки данных проводится кривая наилучшего приближения. Дисперсия в какой-то момент достигает максимума и остается постоянной (выявляется предельный радиус корреляции).

Интерполяция методом кригинга в большинстве случаев дает хорошие результаты, даже когда плотность исходных точек не велика. Однако, при некотором расположении точек возможно появление резких пиков и впадин.

Метод обратных взвешенных расстояний. Этот метод основан на предположении, что чем ближе друг к другу находятся исходные точки, тем ближе их значения. Для точного описания топографии набор точек, по которым будет осуществляться интерполяция, необходимо выбирать в некоторой окрестности определяемой точки, так как они оказывают наибольшее влияние на ее высоту. Это достигается следующим образом. Вводится максимальный радиус поиска или количество точек, ближайших по расстоянию от начальной (определяемой) точки. Затем значению высоты в каждой выбранной точке задается вес, вычисляемый в зависимости от квадрата расстояния до определяемой точки. Этим достигается, чтобы более близкие точки вносили больший вклад в определение интерполируемой высоты по сравнению с более удаленными точками.

Тренд интерполяция. В некоторых случаях исследователя интересуют общие тенденции поверхности, которые характеризуются поверхностью тренда.

Аналогично методу обратных взвешенных расстояний для поверхности тренда используется набор точек в пределах заданной окрестности. В пределах каждой окрестности строится поверхность наилучшего приближения на основе математических уравнений, таких как полиномы или сплайны.

Поверхности тренда могут быть плоскими, показывая общую тенденцию или более сложными. Тип используемого уравнения или степень полинома определяет величину волнистости поверхности. Например, поверхность тренда первого порядка будет выглядеть как плоскость, пересекающая под некоторым углом всю поверхность. Если поверхность имеет один изгиб, то такую поверхность называют поверхностью тренда второго порядка.

Сплайн интерполяция. Возможность описания сложных поверхностей с помощью полиномов невысоких степеней определяется тем, что при сплайн интерполяции вся территория разбивается на небольшие непересекающиеся участки. Аппроксимация полиномами осуществляется раздельно для каждого участка. Обычно используют полином третьей степени - кубический сплайн. Затем строится общая функция «склейки» на всю область, с заданием условия непрерывности на границах участков и непрерывности первых и вторых частных производных, т.е. обеспечивается гладкость склеивания полиномов.

Сглаживание сплайн-функциями особенно удобно при моделировании поверхностей, осложненных разрывными нарушениями, и позволяет избежать искажения типа «краевых эффектов».