
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
П. 6. Смешанные задачи на прямую и плоскостьСодержание книги
Поиск на нашем сайте
Задача 1. Дана плоскость Найти угол между прямой и плоскостью.
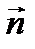 и и 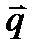 направлены в направлены в
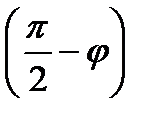 , если , если
же векторы ними равен
или
Задача 2. Дана плоскость Найти расстояние d от точки М 0 до плоскости (α).
Решение.
Проведем прямую (а) с направляющим вектором
Пусть прямая и плоскость пересекаются в точке Е. Тогда Найдем координаты точки Е. Так как это точка пересечения прямой и плоскости, то ее координаты – решение системы Подставим выражения для x, y, z в 4-ое уравнение системы, получим:
Подставим известное t 0 в выражения для x, y, z, т.е. в первые три уравнения системы:
Следовательно, координаты точки Е:
Примеры.
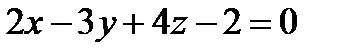 , проходящей через точку М0 (0, 0, 1/2). , проходящей через точку М0 (0, 0, 1/2).
Нормальный вектор плоскости коллинеарен направляющему вектору прямой вектора прямой пропорциональны (совпадают) с координатами нормального вектора. Подставим данные в каноническое уравнение: Ответ: Задача 2. Найти точку пересечения прямой Решение. Координаты точки пересечения М – это решение системы Запишем уравнение прямой в параметрическом виде:
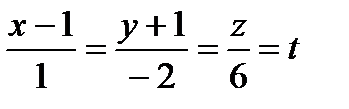 , отсюда , отсюда 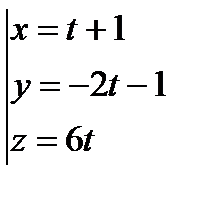 . .
Найдем решение системы:
отсюда х = 1+1=2, у = -2 - 1= -3, z = 6 – координаты точки пересечения. Ответ: Задача 3. Найти угол Решение.
Задача 4. Написать уравнение проекции прямой l: Решение.
 , , 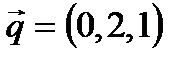 . .
 , ,
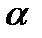 . .
Пересечение полученной плоскости с плоскостью прямая d - и будет искомой проекцией. Уравнение плоскости Тогда общее уравнение искомой прямой d имеет вид: Запишем это уравнение в каноническом виде. Для этого необходимо найти точку А, лежащую на прямой, и направляющий вектор Найдем координаты точки А: пусть z = 0, тогда х = 0, у =-1. Координаты точки А (0, -1, 0). Направляющий вектор Уравнение прямой d – уравнение искомой проекции имеет вид:
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 284; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |

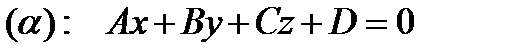 с нормальным вектором
с нормальным вектором 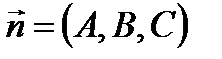 и прямая
и прямая 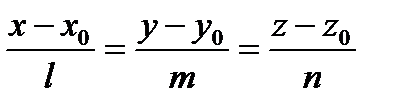 с направляющим вектором
с направляющим вектором  , которая пересекает плоскость в некоторой точке Е.
, которая пересекает плоскость в некоторой точке Е.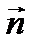
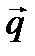
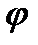
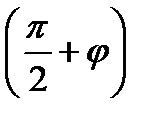 . Таким образом,
. Таким образом,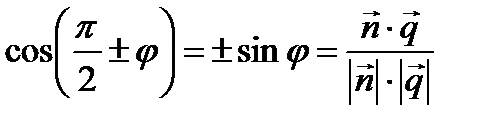 ,
,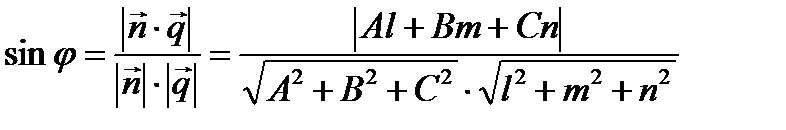 (1)
(1) , не принадлежащая плоскости.
, не принадлежащая плоскости. α
α
 α
α
 , проходящую через точку М 0 перпендикулярно к плоскости (α). Ее уравнение:
, проходящую через точку М 0 перпендикулярно к плоскости (α). Ее уравнение: 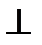 (α), то верно, что
(α), то верно, что 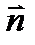
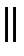
 . Тогда можем записать, что
. Тогда можем записать, что 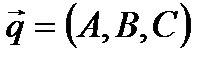 и уравнение прямой примет вид:
и уравнение прямой примет вид: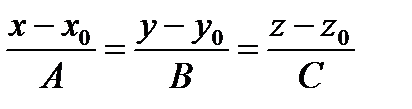 или в параметрическом виде
или в параметрическом виде 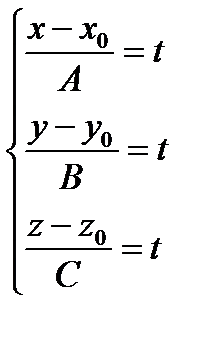 .
.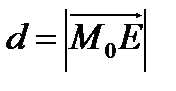 .
.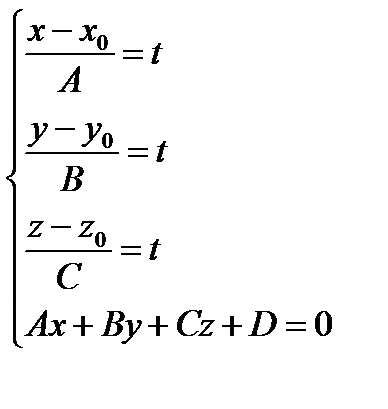 . Перепишем ее в виде
. Перепишем ее в виде 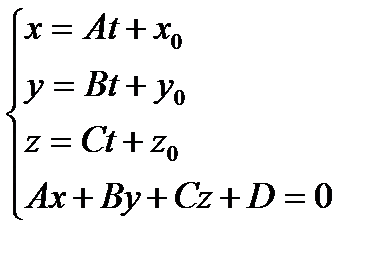 .
.

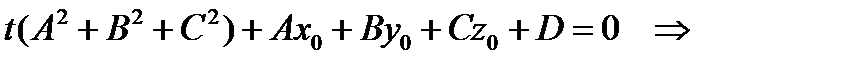
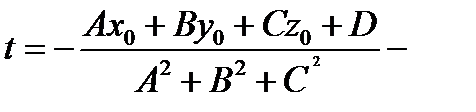 число, пусть t = t 0.
число, пусть t = t 0. ,
,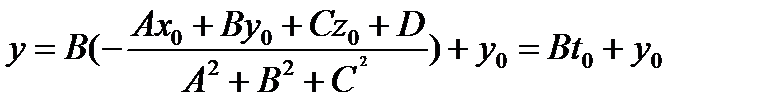 ,
,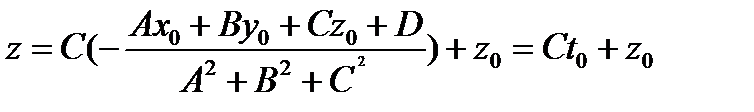 .
.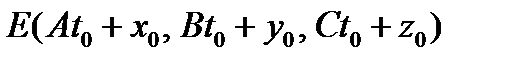 . Тогда координаты вектора
. Тогда координаты вектора 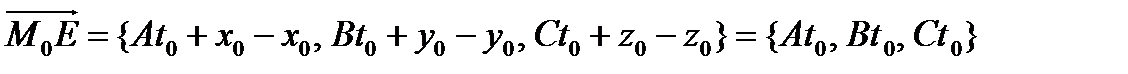 . Найдем
. Найдем  = (подставим вместо t 0 его значение) =
= (подставим вместо t 0 его значение) = 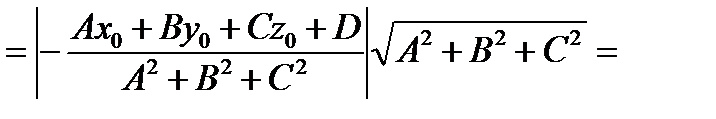
 .
. – расстояние от точки
– расстояние от точки 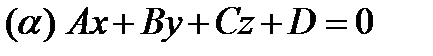 (2)
(2) α
α
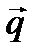
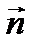
 . Следовательно, координаты направляющего
. Следовательно, координаты направляющего
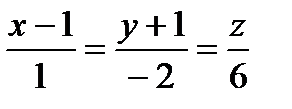 и плоскости
и плоскости 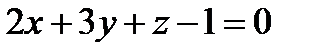 .
.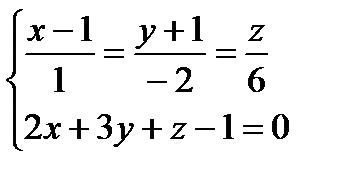 .
.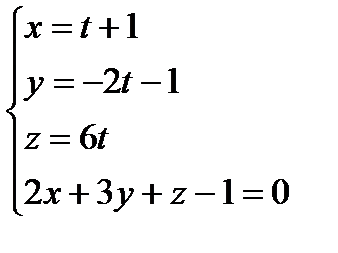
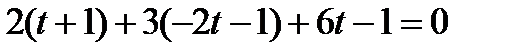
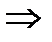
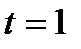 ,
,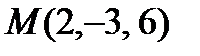 .
.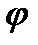 между прямой в:
между прямой в:  и плоскостью
и плоскостью  .
. ,
, 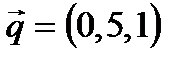 . Угол между прямой и плоскостью находится по формуле:
. Угол между прямой и плоскостью находится по формуле: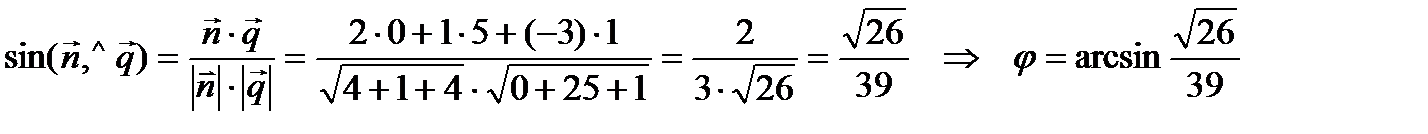 .
.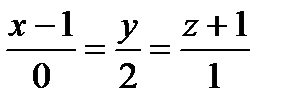 на плоскость
на плоскость 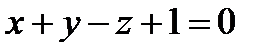 .
.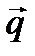 α
α
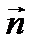
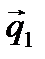 А
А
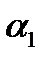 , походящей через прямую l перпендикулярно плоскости
, походящей через прямую l перпендикулярно плоскости  . Нормальный вектор
. Нормальный вектор  .
.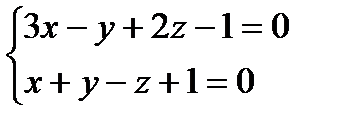 .
. 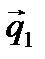 .
.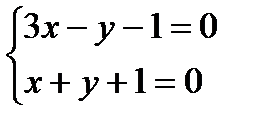 , методом Гаусса получим, что
, методом Гаусса получим, что найдем по формуле:
найдем по формуле: 
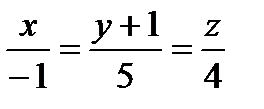 .
.


