
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Растяжение – сжатие стержней . Продольная сила.Содержание книги Поиск на нашем сайте
Растяжение – вид деформации, при котором в поперечном сечении стержня возникает внутренняя продольная сила N, при этом длина увеличивается, а ширина уменьшается.
Для определения продольной внутренней силы N используют метод сечений. Условимся считать эту силу положительной (т.е. присвоим знак «+»), если она растягивает стержень, и отрицательной – если сжимает – правило знаков. Для определения N в произвольном сечении x стержня а) рассмотрим равновесие верхней отсеченной части б). Составляем уравнение равновесия -F+N=0 F=N Знак «+» показывает, что стержень растянут. Эпюра продольных сил. Для суждения о прочности стержня нужно знать продольную силу в любой точке.
Участок – некоторая длина стержня, на котором отсутствует изменение площади или сил. Пример. Пусть стержень ОАВ нагружен силами в сечении
Напряжения. Сила N, приложенная в центре тяжести произвольного сечения стержня является равнодействующей внутренних сил, действующих на бесконечно малой площади dA поперечного сечения площади А и
В пределах действия закона Гука (
При сжатии стержня напряжение имеют лишь другой (отрицательный) знак (нормальная сила направлена в тело стержня). Деформация. Стержень постоянного сечения площадью А под действием осевых растягивающих сил удлиняется на величину Относительное удлинение – удлинение отнесенное к первоначальной длине стержня
При растяжении (сжатии) возникает не только продольная, но и поперечная деформация стержня Отношение поперечной деформации к продольной
|
|||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 103; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.42.59 (0.006 с.) |

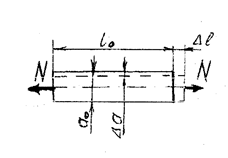 В условиях растяжения будет находиться стержень под действием осевых сил на краях (а). Равнодействующая системы равна F.
В условиях растяжения будет находиться стержень под действием осевых сил на краях (а). Равнодействующая системы равна F.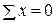 , подставляя значения получим
, подставляя значения получим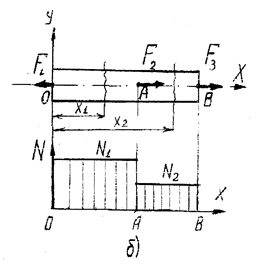 График (эпюру) изменения внутренних сил стоит на линии проведенной параллельно оси стержня. Каждая ордината эпюры равна N.
График (эпюру) изменения внутренних сил стоит на линии проведенной параллельно оси стержня. Каждая ордината эпюры равна N.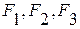 и имеет 2 участка ОА и АВ, на них выбраны сечения на расстоянии
и имеет 2 участка ОА и АВ, на них выбраны сечения на расстоянии 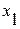 и
и 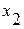 от начала координат. В сечении
от начала координат. В сечении 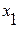 продольная сила
продольная сила 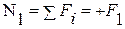
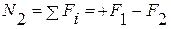
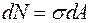 . Тогда,
. Тогда,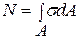
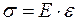 ) плоские поперечные сечения стержня при деформации смещаются параллельно начальному положению, оставаясь плоскими (гипотеза плоских сечений), тогда норм. напряжение во всех точках сечения одинаково, т.е.
) плоские поперечные сечения стержня при деформации смещаются параллельно начальному положению, оставаясь плоскими (гипотеза плоских сечений), тогда норм. напряжение во всех точках сечения одинаково, т.е. 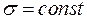 (гипотеза Бернулли) и тогда
(гипотеза Бернулли) и тогда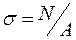
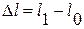 , где
, где 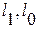 - длины стержня в деформированном и не деформированном состоянии. Это приращение длины называется полным или абсолютным удлинением.
- длины стержня в деформированном и не деформированном состоянии. Это приращение длины называется полным или абсолютным удлинением.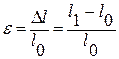 назыв. линейной деформацией. Измеряется ε в %.
назыв. линейной деформацией. Измеряется ε в %.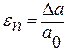 , где а – поперечный размер.
, где а – поперечный размер.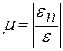 взятое по абсолютной величине, называется коэффициентом Пуассона.
взятое по абсолютной величине, называется коэффициентом Пуассона.


