
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление несобственного интеграла 2-го рода. ⇐ ПредыдущаяСтр 2 из 2
Случай функции с особой точкой
Таким образом, Примеры.
Рассмотрим интегралы
Рассмотрим случай интеграла с особой точкой в левом конце отрезка:
Случай
Аналогично рассматривается интеграл с особой точкой в правом конце отрезка. Таким образом
Исследование несобственных интегралов 2-го рода на сходимость. Признаки сходимости: 1. Признак сравнения: пусть a. Если b. Если 2. Предельный признак сравнения. Пусть для Тогда 3. Если сходится Примеры. 1.
При
2.
При
Замечание: если
(для первого и второго интегралов в правой части особой точкой является
Пример.
Примеры несобственных интегралов с несколькими особыми точками 1. Исходный интеграл сходится, если сходятся оба интеграла в правой части: a.
b.
(несобственный интеграл 2-го рода a. b. Значит,
a. При b. При Таким образом исходный интеграл расходится. Абсолютная и условная сходимость несобственных интегралов. Рассмотрим несобственный интеграл Опр. Несобственный интеграл Опр. Несобственный интеграл Пример.
Вычисление площадей плоских фигур в декартовых и полярных координатах.
Найдем площадь фигуры, ограниченной линиями Рассмотрим площадь
Сложим по
Т.е.
где Из (1.9.1) получаем:
Замечания: 1.
Рис. 19 2.
Рис. 20
3.
Рис. 21
|
|||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 23; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.31.209 (0.015 с.) |


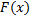 – первообразная для
– первообразная для 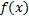
 сходится
сходится 
 конечный предел первообразной
конечный предел первообразной 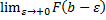 .
.
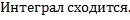

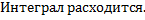



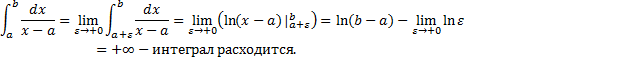
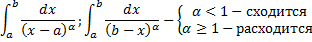
 имеет при
имеет при 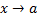 порядок роста
порядок роста 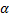 относительно
относительно 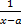 ).
).

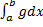 сходится, то
сходится, то  также сходится.
также сходится.
 и
и 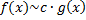 при
при 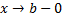 , т.е.
, т.е.  .
.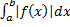 , то сходится и
, то сходится и 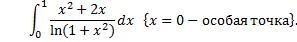
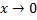
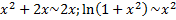 ,
,

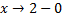


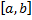 кроме точки
кроме точки  и
и  , тогда
, тогда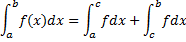
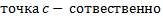 правый или левый конец отрезка).
правый или левый конец отрезка). сходится
сходится 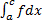 и
и 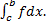

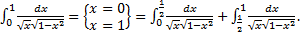
 .
.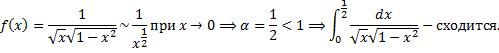
 .
.

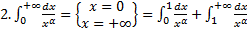 .
. + несобственный интеграл 1-го рода
+ несобственный интеграл 1-го рода  ).
). – сходится при
– сходится при 
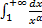 – сходится при
– сходится при 
 расходится для любого
расходится для любого  .
.
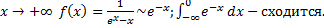
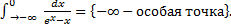
 .
.
 называется абсолютно сходящимся, если сходится интеграл
называется абсолютно сходящимся, если сходится интеграл 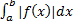 .
.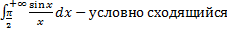 ( без доказательства, см. рис. 17).
( без доказательства, см. рис. 17).


 Вычисление площадей плоских фигур в декартовых координатах
Вычисление площадей плоских фигур в декартовых координатах непрерывна на
непрерывна на  Пусть
Пусть  – разбиение отрезка
– разбиение отрезка 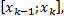
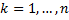 ;
; 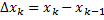 ;
; 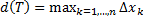 .
.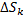 части фигуры, удовлетворяющей условию
части фигуры, удовлетворяющей условию  . Пусть
. Пусть 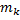 и
и 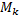 – соответственно наименьшее и наибольшее значения функции
– соответственно наименьшее и наибольшее значения функции 
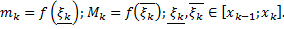
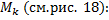


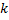 от
от 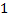 до
до 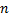 :
: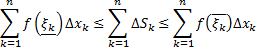

 – интегральные суммы, соответствующие разбиению
– интегральные суммы, соответствующие разбиению  и
и 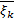 соответственно (нижняя и верхняя интегральные суммы Дарбу); при
соответственно (нижняя и верхняя интегральные суммы Дарбу); при 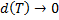


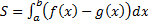 (см. рис. 19.)
(см. рис. 19.)
 (см. рис. 20).
(см. рис. 20).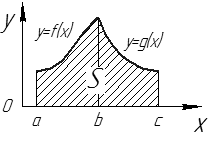
 (см. рис. 21).
(см. рис. 21).



