
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Олимпиада по математике тусур, 2019. Найти все действительные решения уравнения:.Содержание книги
Поиск на нашем сайте
Курс задача 2 Найти все действительные решения уравнения: Решение. Преобразуем, сведя к виду: Тогда Если
Ответ. 2 и 3. Олимпиада по математике ТУСУР, 2019 Курс задача 3 Прямая а прямая Найти параметр Решение. Из строения знаменателей дробей этих канонических уравенений видно, что все направляющие векторы прямых совпадают. Найдём уравнение плоскости
Итак, второй направляющий вектор плосокости: Теперь через точку
Нормаль к плоскости При
Ответ.
Олимпиада по математике ТУСУР, 2019 Курс задача 4 На графике
Решение.
Найдём экстремум этой величины по
При этом Теперь найдём
Олимпиада по математике ТУСУР, 2019 Курс задача 5 Два космических аппарата взлетают вертикально с одинаковой скоростью из разных точек на планете, которая является шаром радиуса
Решение. На чертеже,
Расстояние
Ответ.
Олимпиада по математике ТУСУР, 2019 Курс задача 6 Пусть наклон оси планеты - угол
Решение.
Сферический угол DBC зависит от широты местности и равен По теореме синусов для сферического треугольника верно равенство: (синус угла, соотв. дуге, пропорционален синусу противолежащего угла). В частности, в нашем случае Для решения достаточно лишь первой пропорции.
Для сведения. Возможно и другое решение. Повернём сферу, так, чтобы пусть Солнца во время равноденствия занимал горизонтальную окружность максимального радиуса, а во время солнцестояния - на угол
Примечание. 1. Например, для Земли
|
||||||||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 117; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.154.248 (0.007 с.) |

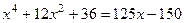 .
. .
. 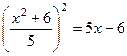 , то есть
, то есть 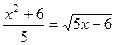 .
.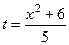 то
то 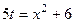 ,
, 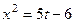 ,
, 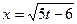 . Таким образом, в равенстве
. Таким образом, в равенстве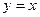 . Значит, нам достаточно решить уравнение
. Значит, нам достаточно решить уравнение 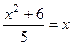 .
.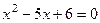 ,
, 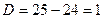 , корни
, корни 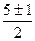 , то есть 2 и 3.
, то есть 2 и 3.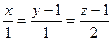 является проекцией прямой
является проекцией прямой 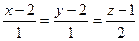 на плоскость
на плоскость 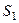 ,
,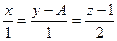 является проекцией этой же прямой на плоскость
является проекцией этой же прямой на плоскость 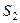 .
.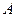 , при котором плоскости
, при котором плоскости 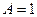 частный случай для плоскости
частный случай для плоскости 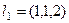 .
Точка
.
Точка 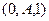 принадлежит прямой, являющейся проекцией.
Точка
принадлежит прямой, являющейся проекцией.
Точка 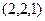 принадлежит той прямой, которая проецируется.
Вектор
принадлежит той прямой, которая проецируется.
Вектор  соединяет эти точки. Тогда плоскость, содержащая обе прямые, и проецируемую, и её проекцию (на чертеже эта плоскость расположена вертикально) имеет два образующих вектора:
соединяет эти точки. Тогда плоскость, содержащая обе прямые, и проецируемую, и её проекцию (на чертеже эта плоскость расположена вертикально) имеет два образующих вектора: 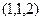 и
и 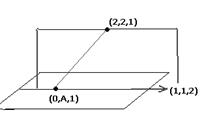
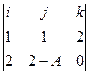 =
= 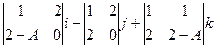 =
= 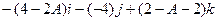 =
=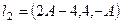 .
. проведём плоскость.
проведём плоскость.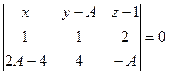
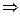

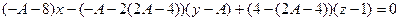
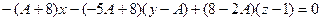
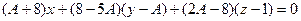
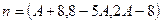 .
.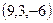 , можно сократить в 3 раза и рассматривать вектор
, можно сократить в 3 раза и рассматривать вектор 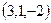 . Осталось узнать, при каком
. Осталось узнать, при каком 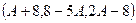 и
и 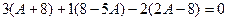
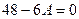
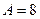 .
.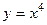 при произвольном
при произвольном 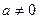 могут быть взяты 3 точки с абсциссами 0,
могут быть взяты 3 точки с абсциссами 0, 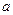 ,
, 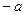 , через них проведена окружность. Найти минимально возможный диаметр окружностей, построенных таким способом.
, через них проведена окружность. Найти минимально возможный диаметр окружностей, построенных таким способом. . Тогда расстояние от точки
. Тогда расстояние от точки 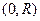 до точек
до точек 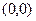 ,
,  и
и 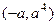 равно
равно 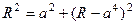

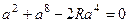
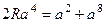
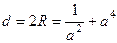 .
.
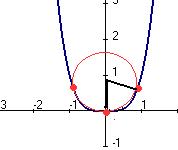
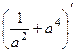 =
= 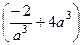 = 0
= 0 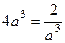
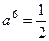
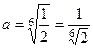 .
.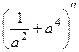 =
= 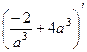 =
= 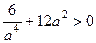 , поэтому минимум, а не максимум.
, поэтому минимум, а не максимум.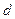 .
. 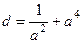 =
= 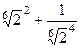 =
= 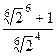 =
=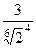 =
= 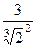 =
=  . Ответ.
. Ответ. 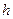 и стали находиться в пределах прямой видимости друг друга. Каково расстояние между ними в этот момент времени?
и стали находиться в пределах прямой видимости друг друга. Каково расстояние между ними в этот момент времени?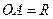 ,
, 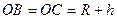 . Два аппарата находятся в точках
. Два аппарата находятся в точках  и
и 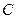 .
.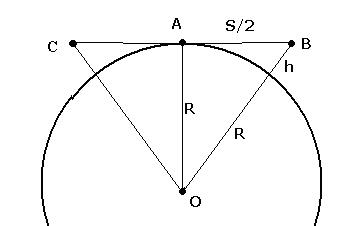
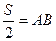 , это половина искомого расстояния. По теореме Пифагора,
, это половина искомого расстояния. По теореме Пифагора,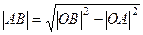 =
= 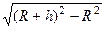 =
= 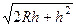 . Тогда
. Тогда 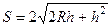 =
= 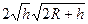 .
.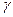 ,
, 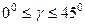 . Найти широту
. Найти широту 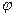 (в северном полушарии), на которой точка восхода Солнца в день солнцестояния отклоняется от востока ровно на
(в северном полушарии), на которой точка восхода Солнца в день солнцестояния отклоняется от востока ровно на 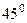 , т.е. например, восход в день зимнего солнцестояния на юго-востоке.
, т.е. например, восход в день зимнего солнцестояния на юго-востоке.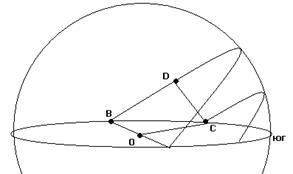
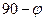 (на экваторе солнце восходит вертикально, ближе к полюсу почти горизонтально). Угол BDC=900 по построению, это перпендикуляр из точки С на дугу BD.
(на экваторе солнце восходит вертикально, ближе к полюсу почти горизонтально). Угол BDC=900 по построению, это перпендикуляр из точки С на дугу BD.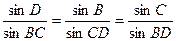
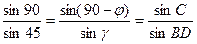 .
.

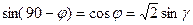
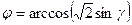 . Ответ.
. Ответ. 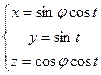 Надо, чтобы при
Надо, чтобы при 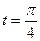 достигалось
достигалось 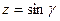 .
.
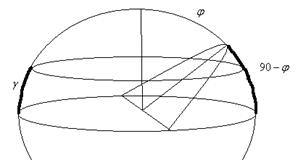
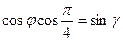
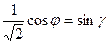
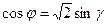
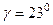 ,
, 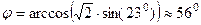 , т.е. явление наблюдается на широте Томска. Если было бы
, т.е. явление наблюдается на широте Томска. Если было бы 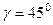 то
то 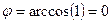 , т.е. на экваторе.
, т.е. на экваторе.


