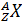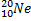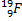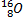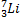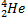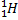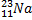Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методические указания к выполнению расчётно-графических работ (ргр)Содержание книги
Поиск на нашем сайте
Содержание
Предисловие Выполнение расчётно - графических работ предусмотрено учебными планами для студентов естественно-технических направлений и специальностей, обучающихся в МГТУ. Настоящие учебно- методические материалы включают шесть РГР, которые в соответствии с рабочими программами по дисциплине физика выполняются в следующем порядке: I курс, I семестр - РГР №1 «Физические основы механики», РГР №2 «Основы молекулярной физики и термодинамики»; I курс, II семестр - РГР №3 «Электростатика. Постоянный электрический ток»; РГР №4 «Электромагнетизм»; II курс, III семестр - РГР №5 «Колебания и волны. Оптика», РГР №6 «Основы квантовой физики. Физика атомного ядра и элементарных частиц».
Содержание расчётно-графических работ РГР №1 «Физические основы механики» Кинематика материальной точки 1. Движение материальной точки задано уравнениями: x = At 2 + B, м; y = Ct 2 1). модули скорости и ускорения точки в момент времени t 2). путь, пройдённый точкой за промежуток времени t 1 = F, c до t 2 = K, c; 3). среднюю скорость точки в промежуток времени t 1 = F, c до t 2 = K, c; Траекторию движения точки. 5). построить графики зависимости скорости, ускорения и пути, пройдённого точкой, от времени;
Числовые значения параметров задачи
2. Радиус-вектор материальной точки относительно начала координат изменяется со временем по закону: 1). получить уравнение траектории точки; 2). построить график траектории точки в промежуток времени от t 0 = 0 до t = 5 c; 3). определить модуль скорости точки в начале координат (x 0, y 0); 4). определить модули тангенциального, нормального и полного ускорений точки в начале координат (x 0 = 0, y 0 = 0); 5). определить радиус кривизны траектории точки в начале координат (x 0, y 0). Числовые значения параметров задачи
3. Твёрдое тело вращается вокруг неподвижной оси Z по закону: Динамика материальной точки 4. Имеется длинный тонкий однородный стержень массой М и длиной l. Материальная частица массой m (m 1). напряжённость 2). потенциалы 3). скорость, ускорение и значение кинетической энергии материальной частицы в точке В; 4). работу, совершённую силами гравитационного поля при перемещении материальной частицы из точки А (x o = l) в точку В (x 1 = b); 5).построить графики зависимости напряжённости и потенциала гравитационного поля от расстояния: Примечание: при решении задания учесть, что напряжённость G и потенциал
Числовые значения параметров задачи
Рис. 1. 5. На обод маховика в форме однородного сплошного диска массой m 1 и радиусом R намотана лёгкая нить, к концу которой прикреплён груз массой m 2. Уравнение вращения маховика: 1). тангенциальное ускорение и линейную скорость, нормальное и полное ускорения точек обода маховика; время опускания груза до пола; кинетическую энергию груза в момент удара о пол; 2). угловую скорость и угловое ускорение маховика; 3). силу натяжения нити с грузом; работу силы натяжения по опусканию груза на пол; Основы молекулярной физики 1. В закрытом резервуаре объёмом V находится газ Х. Начальное состояние газа (состояние 1) характеризуется термодинамическими параметрами: масса газа m 1, давление газа Р 1, температура газа Т 1. После того, как в резервуар впустили некоторое количество такого же газа, его состояние (состояние 2) стало характеризоваться следующими термодинамическими параметрами: масса газа m 2, давление газа Р 2, температура газа Т 2. Затем газ изохорно перевели в состояние 3 с термодинамическими параметрами: Р 3и Т 3 = Т 1. Считая газ идеальным, а значения термодинамических параметров V; m 1; Т 1; m 2 и Т 2 известными, найти: 1). значения термодинамических параметров газа в состоянии 1: P 1; в состоянии 2: Р 2 и в состоянии 3: Р 3; массу m 0 молекулы газа, количество молей 2). наиболее вероятную 3). молярные С v, С р и удельные с v, c p теплоёмкости газа, показатель адиабаты 4). среднюю длину свободного пробега < l > молекул газа в состояниях 1 и 2, динамическую вязкость 5). изобразить термодинамическую диаграмму рассматриваемого изохорного процесса в координатах (P, V), (P, T) и (V, T). Числовые значения параметров задачи
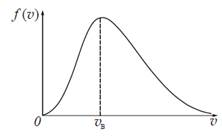
2. Газ Х нагревают от температуры Т 1 до температуры Т 2. Полагая, что функция Максвелла имеет вид f ( 1). используя закон, выражающий распределение молекул идеального газа по скоростям f ( 1.1). вывести формулы средней арифметической < 1.2). рассчитать для каждой из указанных температур значения функции Максвелла при скоростях: а) 1.3). по полученным данным построить график функции f ( 2). используя закон, выражающий распределение молекул идеального газа по скоростям f ( 2.1). получит функцию распределения молекул газа по значениям кинетической энергии поступательного движения 2.2). используя функцию распределения молекул газа по энергиям 3). найти закон, выражающий распределение молекул идеального газа по относительным скоростям f (u, T), где u = 4). для указанных температур определить долю молекул, скорость которых лежит в интервале от 5). ответить на следующие вопросы: а). что собой представляет абсцисса максимума графика функции f (
Рис. 3. б). от чего зависит положение максимума кривой (рис. 3); в). чему численно равна площадь, ограниченная всей кривой (рис. 3); г). в какую сторону вдоль оси абсцисс сместится максимум графика функции f ( д). в какую сторону вдоль оси абсцисс сместится максимум графика функции f ( е). как изменится площадь под кривой (рис. 3) с увеличением числа молекул газа? Газ Х считать идеальным; независимо от характера процесса начальное и конечное состояния газа считать равновесными. Числовые значения параметров задачи
3. 1). построить график цикла и определить: 2).изменение внутренней энергии газа в каждом из рассматриваемых термодинамических процессов и в целом за цикл; 3). работу газа в рассматриваемых термодинамических процессах и в целом за цикл; Электростатика РГР №4 «Электромагнетизм» 1. Электрон в водородоподобном ионе 1). силу I эквивалентного кругового тока при движении электрона вокруг ядра атома; 2). магнитный момент Pm эквивалентного кругового тока; орбитальный механический момент Le электрона; гиромагнитное отношение g орбитальных моментов (отношение числового значения орбитального магнитного момента Pm электрона к числовому значению его орбитального механического момента Le); 3). магнитную индукцию В 1 поля, создаваемого электроном в центре круговой орбиты; 4). изменение Δ 5). изменение магнитного момента электрона Δ Pm, обусловленное изменением его угловой скорости Δ
Числовые значения параметров задачи
2. По квадратной проволочной рамке со стороной а и сопротивлением R течёт электрический ток силой I. 1.1. Определить: 1). напряжённость Н 1 и индукцию В 1 магнитного поля в центре рамки;
2). магнитный момент Pm рамки с током; Рассматриваемая рамка помещена в однородное магнитное поле с индукцией В 2. Нормаль к плоскости рамки составляет с направлением магнитного поля угол Определить: 3). магнитный поток Ф m, пронизывающий рамку; 4). вращающий момент М, действующий на рамку; работу А, которую необходимо затратить для поворота рамки относительно оси, проходящей через середину её противоположных сторон, на угол 5). заряд Q, который пройдет по рамке при изменении угла между нормалью к рамке и линиями магнитной индукции от 0 до Рис. 3. Содержание
Предисловие Выполнение расчётно - графических работ предусмотрено учебными планами для студентов естественно-технических направлений и специальностей, обучающихся в МГТУ. Настоящие учебно- методические материалы включают шесть РГР, которые в соответствии с рабочими программами по дисциплине физика выполняются в следующем порядке: I курс, I семестр - РГР №1 «Физические основы механики», РГР №2 «Основы молекулярной физики и термодинамики»; I курс, II семестр - РГР №3 «Электростатика. Постоянный электрический ток»; РГР №4 «Электромагнетизм»; II курс, III семестр - РГР №5 «Колебания и волны. Оптика», РГР №6 «Основы квантовой физики. Физика атомного ядра и элементарных частиц».
Методические указания к выполнению РАСЧЁТНО-ГРАФИЧЕСКИХ РАБОТ (РГР)
I. При выполнении РГР студенту необходимо руководствоваться следующим: 1. РГР выполняются в 12-ти листовой тетради, на обложке которой приводятся сведения по образцу:
2. Номер варианта задания соответствует порядковому номеру фамилии студента в журнале учебной группы. 3. РГР выполняются чернилами (шариковой ручкой). Для замечаний преподавателя оставляются поля. Условия заданий записываются полностью. Каждое задание должна начинаться с новой страницы. 4. Решения должны сопровождаться исчерпывающими, но краткими объяснениями, раскрывающими физический смысл употребляемых формул и законов. 5. Задания решать в общем виде, т.е. выражать искомую величину через буквенные обозначения величин, заданных в условии задания. Сопоставить размерности левой и правой частей полученной формулы. 6. Подставить в рабочую формулу все величины, выраженные в СИ. Произвести вычисления и получить численное значение искомой величины. Полученное значение записать в ответ. Приближенные числа в ответе записывать в нормальной форме: первая значащая цифра ставится в разряд единиц, а остальные - в десятичные разряды после запятой и полученное число умножается на 10 п, где п — целое положительное или отрицательное число. Например, число 0,0516 в нормальной форме имеет вид 5,16 • 10 -2; число 2170 - 2,17 • 103. Ответ округлять до второй цифры после запятой. 7. В конце работы указать учебники и учебные пособия, которые использовались при решении задач, в т.ч. интернет – ресурс. 8. Работы, оформленные без соблюдения указанных правил не проверяются. 9. При защите РГР необходимо дать устное объяснение решенных заданий и используемых при решении законов. 10. Готовые РГР предоставляются на проверку преподавателю не менее чем за 7 дней до начала зачётно - экзаменационной сессии. II. Критерии и шкала оценивания РГР в соответствии с бально-рейтинговой системой: Каждая расчётно-графическая работа содержит по 5 заданий, включающих по 5 пунктов. Выполнение каждого пункта оценивается от 0 до 2-х баллов согласно критериям, представленным в таблице 1. Таблица 1
Количество баллов, полученные за задания, суммируются. Полученное суммарное значение баллов являются оценкой студента за РГР по БРС. Таблица 2 Перевод баллов в БРС за выполнение РГР в традиционную шкалу оценивания
Содержание расчётно-графических работ
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 229; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.51.35 (0.015 с.) |

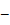 D, м; Z = 0. Определить:
D, м; Z = 0. Определить: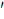 = E, c;
= E, c;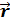 = b t
= b t 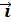 + c
+ c 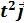 .
.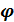 = at
= at 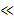 М) в начальный момент времени находится на оси стержня на расстоянии x o = l от одного из его концов (точка А на рис. 1) и имеет начальную скорость, равную нулю (
М) в начальный момент времени находится на оси стержня на расстоянии x o = l от одного из его концов (точка А на рис. 1) и имеет начальную скорость, равную нулю ( 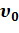 = 0). Определить:
= 0). Определить: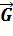 гравитационного поля и силу (модуль F и вектор
гравитационного поля и силу (модуль F и вектор 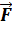 ), действующую на материальную частицу в точке А;
), действующую на материальную частицу в точке А;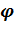 гравитационного поля в точках А (x o = l) и B (x 1 = b) и значения её потенциальной энергии в этих точках;
гравитационного поля в точках А (x o = l) и B (x 1 = b) и значения её потенциальной энергии в этих точках;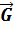 (
( 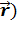 и
и 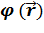 .
.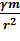 ;
; 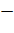
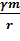 , где
, где 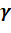 = 6,67
= 6,67  10-11
10-11 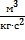 - гравитационная постоянная.
- гравитационная постоянная.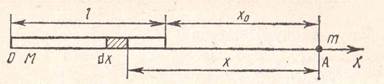
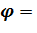
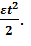 До начала вращения маховика высота груза над полом составляла h (рис. 2). Определить:
До начала вращения маховика высота груза над полом составляла h (рис. 2). Определить: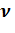 газа, общее число N и концентрацию n молекул газа и плотности
газа, общее число N и концентрацию n молекул газа и плотности 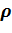 газа в состояниях 1 и 2;
газа в состояниях 1 и 2;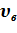 , среднюю <
, среднюю < 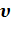 >, среднюю квадратичную <
>, среднюю квадратичную < 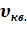 > скорости молекул газа в состояниях 1 и 2; среднюю кинетическую энергии поступательного <
> скорости молекул газа в состояниях 1 и 2; среднюю кинетическую энергии поступательного < 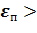 , вращательного <
, вращательного < 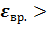 движения молекул газа и среднее значение их полной кинетической энергии <
движения молекул газа и среднее значение их полной кинетической энергии < 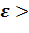 в состояниях 1 и 2;
в состояниях 1 и 2;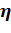 и коэффициент теплопроводности
и коэффициент теплопроводности 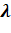 газа;
газа;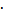 1, кг
1, кг
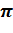 (
( 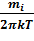 )3/2
)3/2 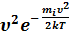 :
: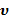 , T):
, T):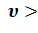 , средней квадратичной <
, средней квадратичной < 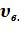 скоростей и определить их числовые значения для температур Т 1 и Т 2;
скоростей и определить их числовые значения для температур Т 1 и Т 2;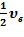 б).
б). 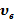 в).
в). 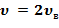 ;
;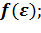
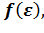 вывести формулы средней кинетической энергии <
вывести формулы средней кинетической энергии < 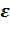 > молекул и наиболее вероятное значение энергии
> молекул и наиболее вероятное значение энергии 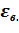 молекул и рассчитать их числовые значения для температур Т 1 и Т 2;
молекул и рассчитать их числовые значения для температур Т 1 и Т 2;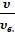 ;
;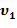 до
до 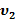 ;
;
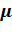 и таким же числом молекул;
и таким же числом молекул;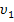 , м/с
, м/с
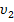 , м/с
, м/с
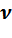 молей газа Х, занимающего объём V 1 и находящегося под давлением Р 1, подвергается изохорному нагреванию до температуры Т 2 = 2 Т 1. После этого газ подвергли изотермическому расширению до начального давления, а затем он в результате изобарного сжатия возвращён в первоначальное состояние.
молей газа Х, занимающего объём V 1 и находящегося под давлением Р 1, подвергается изохорному нагреванию до температуры Т 2 = 2 Т 1. После этого газ подвергли изотермическому расширению до начального давления, а затем он в результате изобарного сжатия возвращён в первоначальное состояние.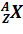 движется по круговой орбите, радиус которой определяется соотношением
движется по круговой орбите, радиус которой определяется соотношением 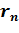 =
= 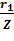 n 2, где r 1 = 0,53
n 2, где r 1 = 0,53 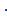 10-31 кг, е = 1,6
10-31 кг, е = 1,6 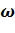 угловой скорости электрона при помещении атома в однородное магнитное поле с индукцией В 2, перпендикулярной плоскости орбиты (рис. 24), учитывая, что Δ
угловой скорости электрона при помещении атома в однородное магнитное поле с индукцией В 2, перпендикулярной плоскости орбиты (рис. 24), учитывая, что Δ 
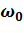 , где
, где 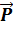 m в обоих случаях.
m в обоих случаях.