
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Корреляционный анализ качественных показателей месторожденияСодержание книги
Поиск на нашем сайте
Выявление закономерностей размещения компонентов по данным эксплуатационного опробования и установление корреляции между компонентами позволяет производить оконтуривание залежи, подсчитывать запасы, прогнозировать геометрию размещения на другие участки, сокращать затраты на производство и рационально планировать горные работы. Данные измерений, опробования залежей графически представляют по линии в виде гистограмм и кумулят. Для построения этих графиков производится группировка значений показателей содержания меди (
где Затем значения исследуемых показателей Подсчитывается число
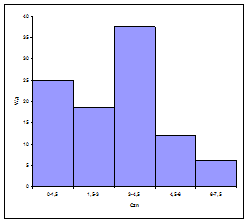
Строятся графики по содержанию меди и цинка – гистограммы и кумуляты, характеризующие вероятное распределение значений показателей. Для построения гистограмм на оси абсцисс отмечаются границы интервалов (классов) и строятся прямоугольники с основаниями, равными длине интервалов, и высотами, равными частостям Производится статистическое оценивание средних значений и расчет величины условного значения класса
где
Вычисляются показатели изменчивости величин - условный момент первого порядка
- условный момент второго порядка
- среднее значение показателя
- среднее квадратическое отклонение (стандарт) значений показателя
- коэффициент вариации значений показателя
Коэффициент вариации количественно выражает степень статистической изменчивости (варьируемости) показателей статистической совокупности. Производится исследование взаимосвязи между объемным содержанием меди и объемным содержанием цинка методом корреляционного анализа сгруппированных данных и заполняется специальный формуляр – корреляционная таблица. Для оценки тесноты связи используется коэффициент корреляции, который рассчитывается по формуле
где
По результатам расчетов строится график зависимости между показателями
Точками абсцисс являются средние значения объемного содержания цинка в классовых промежутках, а ординатами соответствующие средние значения объемного содержания меди. Исходные данные по скважинам для корреляционного анализа содержаний по горизонту 480м представлены в таблице 6.10
Таблица 6.10 – Исходные данные
Из таблицы 6.10: Классовый промежуток по содержанию меди
Значение классового промежутка округляем в большую сторону для удобства дальнейших вычислений - Классовый промежуток по содержанию цинка
Значение классового промежутка округляется до Вычисление величин дискретных
Таблица 6.11 – Обработка значений содержания меди
Таблица 6.12 – Обработка значений содержания цинка
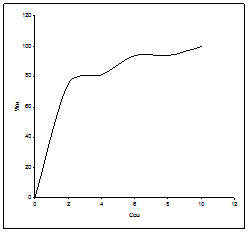
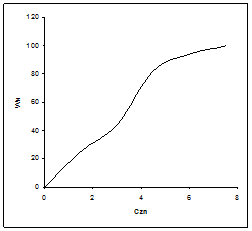
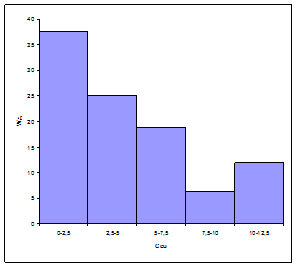
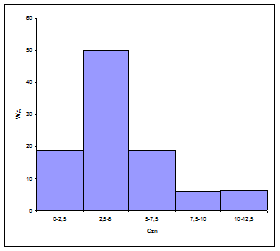
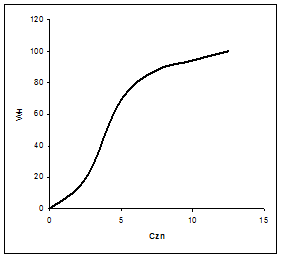
Гистограмма и кумулята, характеризующие вероятное распределение значений показателей, представлены на рисунках 6.15 и 6.16
По объемному содержанию меди за нулевой класс принимается средний классовый промежуток 4 – 6. Среднее значение показателя в нулевом классе
Среднее значение показателя
Следовательно, величина условного значения класса 0 – 2 равна
Аналогично расчет ведется для каждого классового промежутка. Полученные данные условных значений классов сводятся в таблицу 6.13
Таблица 6.13 – Расчет статистических оценок объемного содержания меди
Аналогичные расчеты производятся по объемному содержанию цинка. За нулевой класс принимается средний классовый промежуток 3 – 4,5. Среднее значение показателя в нулевом классе
Среднее значение показателя
Следовательно, величина условного значения класса 0 – 1,5 равна
Полученные данные условных значений классов сводятся в таблицу 6.14
Таблица 6.14 – Расчет статистических оценок объемного содержания цинка
Полученные результаты определения статистических оценок показателей
Таблица 6.15 – Определение статистических оценок показателей
Исследуемая взаимосвязь между объемным содержанием меди и объемным содержанием цинка методом корреляционного анализа представлена в таблице 6.16. Полученный коэффициент корреляции
где
График зависимости между показателями
Рисунок 6.17 – Зависимость объемного содержания меди от объемного содержания цинка
Таблица 6.16 – Корреляционная таблица
Исходные данные по скважинам для корреляционного анализа содержаний по горизонту 500м представлены в таблице 6.17
Таблица 6.17 – Исходные данные
Из таблицы 6.17: Классовый промежуток по содержанию меди
Округленное значение классового промежутка – Классовый промежуток по содержанию цинка
Округленное значение классового промежутка – Вычисление величин дискретных
Таблица 6.18 – Обработка значений содержания меди
Таблица 6.19 – Обработка значений содержания цинка
Гистограмма и кумулята, характеризующие вероятное распределение значений показателей, представлены на рисунках 6.18и 6.19
По объемному содержанию меди за нулевой класс принимается средний классовый промежуток 5 – 7,5. Среднее значение показателя в нулевом классе
Среднее значение показателя
Следовательно, величина условного значения класса 0 – 2,5 равна
Полученные данные условных значений классов сводятся в таблицу 6.20
Таблица 6.20 – Расчет статистических оценок объемного содержания меди
Аналогичные расчеты производятся по объемному содержанию цинка. За нулевой класс принимается средний классовый промежуток 5 – 7,5. Среднее значение показателя в нулевом классе
Среднее значение показателя
Следовательно, величина условного значения класса 0 – 2,5 равна
Полученные данные условных значений классов сводятся в таблицу 6.21
Таблица 6.21 – Расчет статистических оценок объемного содержания цинка
Полученные результаты определения статистических оценок показателей
Таблица 6.22 – Определение статистических оценок показателей
Исследуемая взаимосвязь между объемным содержанием меди и объемным содержанием цинка методом корреляционного анализа представлена в таблице 6.23 Полученный коэффициент корреляции
где
График зависимости между показателями
Рисунок 6.20 – Зависимость объемного содержания меди от объемного содержания цинка
Таблица 6.23 – Корреляционная таблица
Исходные данные по скважинам для корреляционного анализа содержаний по вертикальному разрезу 31290 представлены в таблице 6.24
Таблица 6.24 – Исходные данные
Из таблицы 6.24: Классовый промежуток по содержанию меди
Округленное значение классового промежутка - Классовый промежуток по содержанию цинка
Значение классового промежутка округляется до Вычисление величин дискретных
Таблица 6.25 – Обработка значений содержания меди
Таблица 6.26 – Обработка значений содержания цинка
Гистограмма и кумулята, характеризующие вероятное распределение значений показателей, представлены на рисунках 6.21 и 6.22
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 105; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.201.46 (0.008 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

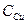 ) и содержания цинка (
) и содержания цинка (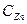 ). При группировке значений показателей определяется классовый промежуток
). При группировке значений показателей определяется классовый промежуток 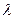 по содержанию меди (
по содержанию меди (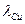 ) и содержанию цинка (
) и содержанию цинка (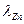 )
)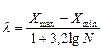 (6.2)
(6.2)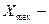 максимальное значение показателя в данных разведки;
максимальное значение показателя в данных разведки; 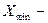 минимальное значение показателя в данных разведки;
минимальное значение показателя в данных разведки;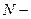 количество данных разведки.
количество данных разведки. равных интервалов (классов) в соответствии с величиной классового промежутка.
равных интервалов (классов) в соответствии с величиной классового промежутка.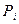 (частота) значений показателей объемного содержания меди и цинка, попавших в каждый интервал. После этого производится последовательное суммирование частот
(частота) значений показателей объемного содержания меди и цинка, попавших в каждый интервал. После этого производится последовательное суммирование частот 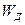 и накопленных
и накопленных  частости по формулам
частости по формулам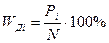 (6.3)
(6.3)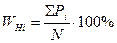 (6.4)
(6.4)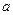 , которая определяется по формуле
, которая определяется по формуле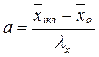 , (6.5)
, (6.5)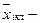 среднее значение показателя в классовом промежутке;
среднее значение показателя в классовом промежутке;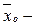 среднее значение показателя в нулевом классе, за нулевой класс принимается средний классовый промежуток;
среднее значение показателя в нулевом классе, за нулевой класс принимается средний классовый промежуток;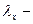 величина классового промежутка.
величина классового промежутка.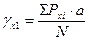 , (6.6)
, (6.6)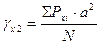 , (6.7)
, (6.7)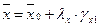 , (6.8)
, (6.8)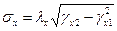 , (6.9)
, (6.9)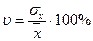 . (6.10)
. (6.10)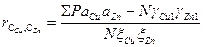 , (6.11)
, (6.11)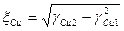 ;
;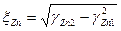 .
.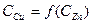 , вычисленная по формуле
, вычисленная по формуле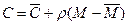 (6.12)
(6.12)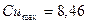 ;
; 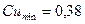 ;
;  ;
; 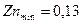 ;
; 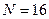 .
.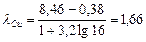
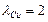 .
.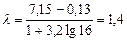
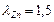 .
.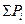
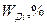
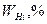
 а
а
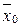 вычисляется путем сложения всех показателей, входящих в данный классовый промежуток и делением на их количество:
вычисляется путем сложения всех показателей, входящих в данный классовый промежуток и делением на их количество: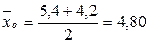
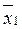 в классовом промежутке 0 – 2 определяется по формуле
в классовом промежутке 0 – 2 определяется по формуле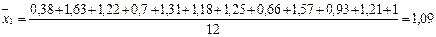
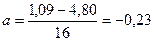
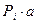

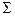
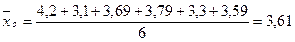
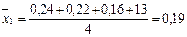
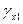
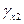
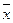
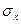
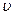
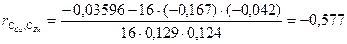 ,
,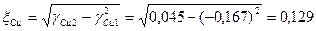 ;
;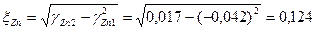 .
.
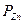
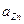
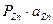
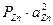

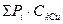
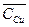
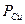
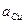
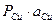
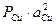
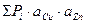
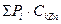
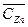
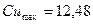 ;
; 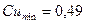 ;
; 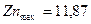 ;
; 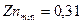 ;
; 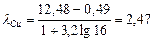
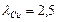 .
.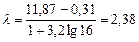
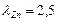 .
. а
а
 б
б
 а
а
 б
б
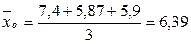
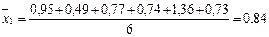
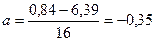
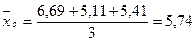
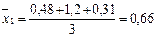
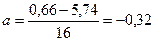
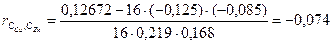
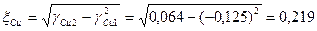 ;
; .
.
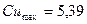 ;
; 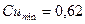 ;
; 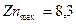 ;
; 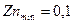 ;
; 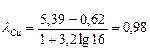
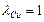 .
.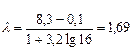
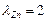 .
.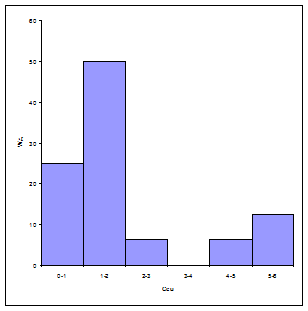 а
а
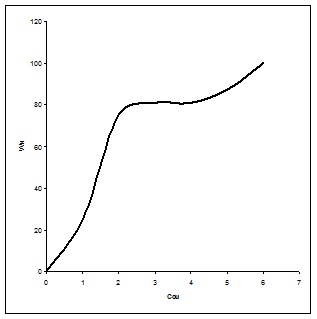 б
б



