
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение байесовского классификатора при классификации документов вузаСодержание книги
Поиск на нашем сайте
Как отмечают многие отечественные [5, 6] и зарубежные [7, 8, 9] авторы, байесовский классификатор является одним из самых простых и эффективных вероятностных методов классификации документов. Пусть имеется множество классов
где Следует отметить, что в формуле (1) знаменатель P (d) можно опустить, так как его значение не зависит от класса c, а значит, не влияет на нахождение наибольшей вероятности Применение байесовского классификатора к задаче классификации текстовых документов предполагает использование машинных методов обучения с учителем. Следовательно, для нахождения значения
где Чтобы оценить вероятность
где вероятность
где Так как целью классификации является нахождение для документа самого вероятного для него класса, то задача байесовского классификатора состоит в нахождении самого вероятного класса c, который рассчитывается по формуле:
Многие авторы [1, 3, 5, 6] среди преимуществ байесовского классификатора отмечают простую программную реализацию и быстроту работы, однако они же отмечают и недостатки метода, к которым относится низкое качество классификации и неспособность учитывать зависимость результата классификации от сочетания признаков. Отмечается [22], что байесовский классификатор может быть рекомендован для небольших размеров выборки из-за присущей ему регуляризации, что делает его менее склонным к чрезмерному приспособлению. Таким образом, байесовский классификатор можно использовать для распознавания документов с «сильными» ключевыми словами и прямыми отношениями между текстовыми признаками и соответствующими классами, например, для простых форм обнаружения рекламного контента. Однако в документах вуза порой сложно выделить ключевые слова, например, в предложениях о сотрудничестве: такие документы слабо структурированы, содержат много информации, слабо поддающейся анализу. Поэтому для документов вуза с неочевидными ключевыми словами и связями между текстовыми признаками и соответствующими классами при использовании байесовского классификатора ожидается ухудшение качества классификации документов.
|
||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 86; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

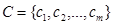 документов. Согласно теореме Байеса вероятность того, что документ принадлежит классу
документов. Согласно теореме Байеса вероятность того, что документ принадлежит классу 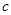 , имеет вид [4]:
, имеет вид [4]: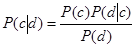 , (1)
, (1)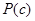 – вероятность того, что документ отнесен к классу c;
– вероятность того, что документ отнесен к классу c; 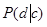 – вероятность встретить документ среди документов класса c; P (d) – вероятность того, что документ можно представить в виде вектора
– вероятность встретить документ среди документов класса c; P (d) – вероятность того, что документ можно представить в виде вектора 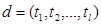 ,
, 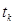 – терм из документа, l – количество термов в документе.
– терм из документа, l – количество термов в документе.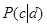 .
.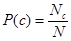 , (2)
, (2)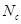 – количество документов в обучающем множестве из класса c; N – общее количество документов в обучающем множестве.
– количество документов в обучающем множестве из класса c; N – общее количество документов в обучающем множестве.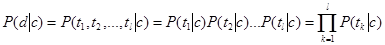 , (3)
, (3)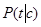 рассчитывается по формуле:
рассчитывается по формуле: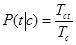 , (4)
, (4)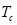 – общее количество термов в документах класса c;
– общее количество термов в документах класса c; 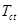 – количество вхождений терма t во всех документах класса c.
– количество вхождений терма t во всех документах класса c.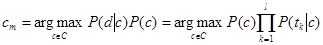 . (5)
. (5)


