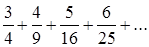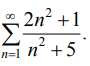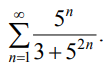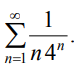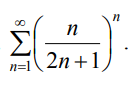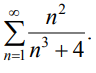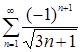Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 10.2. Дифференциальные уравнения высших порядковСодержание книги
Поиск на нашем сайте
Понятие дифференциального уравнения 2-го порядка и его частного и общего решения. Линейное дифференциальное уравнение второго порядка: общее и частное решение. Решение линейных дифференциальных уравнений второго порядка с постоянными коэффициентами.
Литература: 1. Сборник задач и упражнений по высшей математике для студентов экономических специальностей: в 2 ч. / Л.Н.Гайшун, Н.В.Денисенко, А.В.Марков (и др.). – Минск: БГЭУ, 2014. – Ч.2. – 270 с. 2. Шилкина, Е. И. Высшая математика: Часть 2. Учеб.-практ. пособие / Е. И. Шилкина, М. П. Дымков, В. А. Рабцевич. – Мн.: БГЭУ, 2014. – 167 с.
Задачи для самостоятельного решения: 10.2.1. Проинтегрировать дифференциальное уравнение y´´ = 10.2.2. Проинтегрировать дифференциальные уравнения, найти указанные частные решения и построить их. а) y´ = б) y´´ = 2; y(0) = 1; y´(0) = − 2; в) y´´´ = 6; y(0) = 1; y´(0) = 3; y´´(0) = 6.
Задания на межсессионную аттестацию 5.2.1. Написать первые пять членов последовательности 5.2.2. Написать формулу общего члена последовательности
5.2.3. Доказать, пользуясь определением, что число а является пределом последовательности 5.3.1. Доказать, пользуясь определением предела, что
5.3.2. Найти предел функции a) b) c) d) e)
6.1.8. Исходя из определения производной, найти производную функции y = 6.1.9. Найти первую производную следующих функций: 4) y = 5) y = 6) y = 6.1.10. Найти производную сложной функции
y =
6.1.11. Найти производную неявной функции
6.1.12. Найти дифференциалы первого, второго и третьего порядков функции y = 6.1.13. Найти приближенное значение 6.1.14. Найти предел, используя правило Лопиталя
6.2.7. Найти интервалы монотонности функции y = 6.2.8. Найти экстремумы функции y = x· 6.2.9. Найти наибольшее и наименьшее значение функции y = 6.2.10. Найти интервалы выпуклости и точки перегиба функции x 6.2.11. Найти асимптоты кривой y = 6.2.12. Исследовать функцию y = 7.1.1. Вычислить значения частных производных функции u = 7.1.2. Вычислить 7.1.3. Дана функция z =
7.2.1. Исследовать на экстремум функцию двух переменных z = 7.2.2. Методом Лангранжа найти условный экстремум функции z = 8 –
Задания на сессионную аттестацию 8.1.1. Взять неопределенные интегралы а) б) в)
8.1.2. Проинтегрировать методом замены переменной и внесения под знак дифференциала а) б) в) г) д) 8.1.3. Проинтегрировать по частям а) б) в) г) 8.1.4. Проинтегрировать дроби а) б) 8.2.1. Взять определенные интегралы
и) 8.2.2. Вычислить методом подстановки
8.2.3. Вычислить с помощью универсальной тригонометрической подстановки
8.2.4. Вычислить интегрированием по частям
9.2.1. Разложить в ряд Маклорена
9.2.2. Разложить в ряд Тейлора
9.2.3. Вычислить, взяв три члена соответствующего ряда Маклорена и оценить погрешность ε
9.2.4. Разложить функцию в ряд Фурье периодическую (с периодом Т = 2π) функцию f(x), заданную на отрезке [-π; π]. Постройте график данной функции при
10.1.1. Доказать, что решением дифференциального уравнения y´´´ = 10.1.2. Доказать, что функция y = 10.1.3. Установить, является ли функция x² − y² − Cx = 0 общим интегралом дифференциального уравнения 2xyy´ + x² − y² = 0. 10.1.4. Показать, что функция y = x² + C является решением дифференциального уравнения y´ = 2x. Построить семейство интегральных кривых и выделить интегральную кривую, проходящую через точку (2; 3). 10.1.5. Решить дифференциальное уравнение с разделяющимися переменными, найти частное решение
9.1.1. Найти а) б) в)
9.1.2. Исследовать сходимость ряда, используя следствие из необходимого признака сходимости
9.1.3. Исследовать сходимость ряда с помощью признаков сравнения
9.1.4. Исследовать сходимость ряда с помощью признака Даламбера.
9.1.5. Исследовать сходимость ряда по признаку Коши.
9.1.6. Исследовать сходимость ряда с помощью интегрального признака
9.1.7. Выяснить, сходится ряд абсолютно или условно
10.2.1. Проинтегрировать дифференциальное уравнение y´´ = 10.2.2. Проинтегрировать дифференциальные уравнения, найти указанные частные решения и построить их. а) y´ = б) y´´ = 2; y(0) = 1; y´(0) = − 2; в) y´´´ = 6; y(0) = 1; y´(0) = 3; y´´(0) = 6.
Рефераты
Темы рефератов
1. Особые решения дифференциальных уравнений. 2. Ряд Фибоначчи и его приложения. 3. Золотое сечение. 4. Ряд и интеграл Фурье. 5. Математика и жизнь. 6. Дифференциальные уравнения и их приложения. 7. Кратные интегралы и их приложения. 8. Математика и музыка. 9. Интуиция и математика. 10. Приложения рядов к приближенным вычислениям. 11. Причины введения в математику элементов математического анализа. 12. Комплексные числа и жизнь. 13. История введения комплексных чисел. 14. Нужна ли нам теория вероятностей? 15. Статистика как раздел математики. 16. Теория игр. 17. Фракталы и их приложения. 18. Бифуркации и их значения. 19. Несобственные кратные интегралы. 20. Интегралы Коши, Римана, Лебега. 21. Параметрические интегралы. 22. Диофантов язык и десятая проблема Гильберта. 23. Продуктивность и креативность в математике. 24. Конструктивная математика. 25. Топологические пространства.
Требования к оформлению реферата
Объём реферата 20 страниц машинописного текста, шрифт Times New Roman 14, интервал 1,5, выравнивание по ширине, сквозная нумерация страниц, сквозная нумерация рисунков, сквозная нумерация формул, обязательно список литературы – минимум три источника.
|
||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 140; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.97.63 (0.006 с.) |

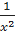 . Найти частное решение, удовлетворяющее начальным условиям: y(1) = 0, y´(1) = 1.
. Найти частное решение, удовлетворяющее начальным условиям: y(1) = 0, y´(1) = 1.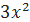 ; y(0) = 2;
; y(0) = 2;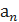 =
= 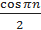 .
.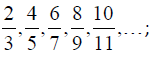
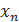 , если
, если  =
= 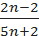 , a =
, a = 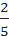 .
.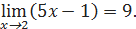
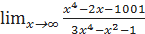 ;
;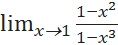 ;
;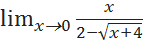 ;
;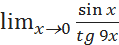 ;
;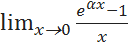 .
.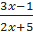 .
.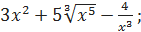
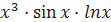 ;
;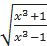 .
.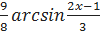 .
.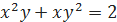 .
.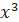 ·lnx.
·lnx.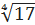 с точностью до двух знаков после запятой.
с точностью до двух знаков после запятой.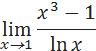
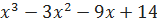 .
.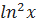 .
.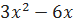 на отрезке
на отрезке 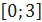 .
.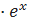 .
.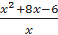 .
.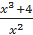 и построить ее график.
и построить ее график.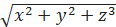 – x·y·z в точке М(2; –2; 1).
– x·y·z в точке М(2; –2; 1).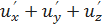 в точке
в точке 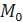 (1, 1, 1), если u = ln(1 + x +
(1, 1, 1), если u = ln(1 + x + 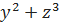 ).
).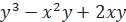 , точка
, точка 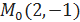 и вектор
и вектор 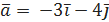 . Требуется найти производную функцию z в точке
. Требуется найти производную функцию z в точке 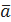 и градиент функции в данной точке.
и градиент функции в данной точке.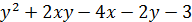 .
.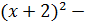
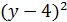 , если ее аргументы связаны уравнением x + 3y = 0.
, если ее аргументы связаны уравнением x + 3y = 0.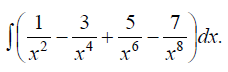
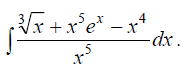
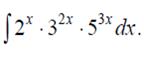
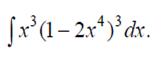
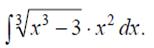
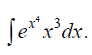
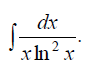
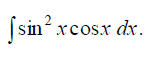
 ;
;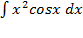 ;
;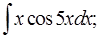
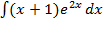 .
.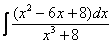
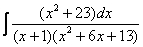
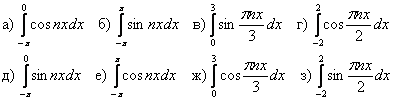
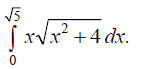
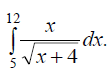
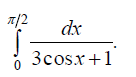
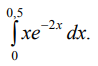
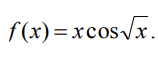

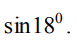
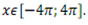
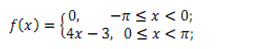
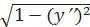 является функция y = − sin x + 2x + C.
является функция y = − sin x + 2x + C.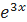 является решением дифференциального уравнения y´´´ − 3y´ − 18y = 0.
является решением дифференциального уравнения y´´´ − 3y´ − 18y = 0.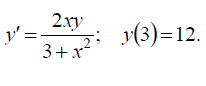
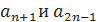 члены ряда:
члены ряда: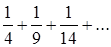 ;
; 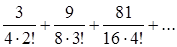 ;
;