
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 5. Введение в математический анализ (ii семестр)Содержание книги
Поиск на нашем сайте
Высшая математика, МЗР-1
Содержание дисциплины
РАЗДЕЛ 5. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ (II СЕМЕСТР) Тема 5.2. Числовые последовательности Понятие числовой последовательности и ее предела. Общие свойства сходящихся последовательностей. Бесконечно малые и бесконечно большие последовательности. Существование предела монотонной ограниченной последовательности. Предельный переход при арифметических операциях над пределами. Число е, натуральные логарифмы.
Литература: Высшая математика. Практикум, Ч. 1 / А. В. Конюх, С. В. Майоровская, О. Н. Поддубная, В. А. Рабцевич. – Минск: [б. и.], 2014. – 274 с.
Задачи для самостоятельного решения: 5.2.1. Написать первые пять членов последовательности 5.2.2. Написать формулу общего члена последовательности
5.2.3. Доказать, пользуясь определением, что число а является пределом последовательности
Тема 5.3. Предел и непрерывность функции Определение предела функции в точке. Односторонние пределы функции одной переменной. Бесконечно малые и бесконечно большие функции, их сравнение. Свойства сходящихся в точке функций: ограниченность функции в окрестности точки схождения, действия над сходящимися функциями. Эквивалентные функции, их использование при определении предела отношения функций. Первый и второй замечательные пределы. Таблица важнейших пределов. Определение пределов степенно-показательных функций. Непрерывность функции. Определение и классификация точек разрыва. Кусочно-непрерывные функции.
Литература: Высшая математика. Практикум, Ч. 1 / А. В. Конюх, С. В. Майоровская, О. Н. Поддубная, В. А. Рабцевич. – Минск: [б. и.], 2014. – 274 с.
Задачи для самостоятельного решения: 5.3.1. Доказать, пользуясь определением предела, что
5.3.2. Найти предел функции a) b) c) d) e)
РАЗДЕЛ 6. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ (II СЕМЕСТР)
РАЗДЕЛ 7. ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ (II СЕМЕСТР)
РАЗДЕЛ 8. ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ (II СЕМЕСТР)
РАЗДЕЛ 9. РЯДЫ
Тема 9.1. Числовые ряды Определение числового ряда и его суммы. Прогрессии. Необходимое условия сходимости, критерий Коши сходимости числового ряда. Гармонический ряд, его расходимость. Достаточные условия сходимости рядов с положительными членами. Признак Даламбера. Радикальный интегральный признак Коши. Знакопеременные числовые ряды, абсолютная и условная сходимость. Знакочередующиеся ряды, признак сходимости.
Литература: 1. Сборник задач и упражнений по высшей математике для студентов экономических специальностей: в 2 ч. / Л.Н.Гайшун, Н.В.Денисенко, А.В.Марков (и др.). – Минск: БГЭУ, 2014. – Ч.2. – 270 с. 2. Шилкина, Е. И. Высшая математика: Часть 2. Учеб.-практ. пособие / Е. И. Шилкина, М. П. Дымков, В. А. Рабцевич. – Мн.: БГЭУ, 2014. – 167 с.
Задачи для самостоятельного решения: 9.1.1. Найти а) б) в)
9.1.2. Исследовать сходимость ряда, используя следствие из необходимого признака сходимости
9.1.3. Исследовать сходимость ряда с помощью признаков сравнения
9.1.4. Исследовать сходимость ряда с помощью признака Даламбера.
9.1.5. Исследовать сходимость ряда по признаку Коши.
9.1.6. Исследовать сходимость ряда с помощью интегрального признака
9.1.7. Выяснить, сходится ряд абсолютно или условно
Задания на межсессионную аттестацию 5.2.1. Написать первые пять членов последовательности 5.2.2. Написать формулу общего члена последовательности
5.2.3. Доказать, пользуясь определением, что число а является пределом последовательности 5.3.1. Доказать, пользуясь определением предела, что
5.3.2. Найти предел функции a) b) c) d) e)
6.1.8. Исходя из определения производной, найти производную функции y = 6.1.9. Найти первую производную следующих функций: 4) y = 5) y = 6) y = 6.1.10. Найти производную сложной функции
y =
6.1.11. Найти производную неявной функции
6.1.12. Найти дифференциалы первого, второго и третьего порядков функции y = 6.1.13. Найти приближенное значение 6.1.14. Найти предел, используя правило Лопиталя
6.2.7. Найти интервалы монотонности функции y = 6.2.8. Найти экстремумы функции y = x· 6.2.9. Найти наибольшее и наименьшее значение функции y = 6.2.10. Найти интервалы выпуклости и точки перегиба функции x 6.2.11. Найти асимптоты кривой y = 6.2.12. Исследовать функцию y = 7.1.1. Вычислить значения частных производных функции u = 7.1.2. Вычислить 7.1.3. Дана функция z = 7.2.1. Исследовать на экстремум функцию двух переменных z = 7.2.2. Методом Лангранжа найти условный экстремум функции z = 8 –
Задания на сессионную аттестацию 8.1.1. Взять неопределенные интегралы а) б) в)
8.1.2. Проинтегрировать методом замены переменной и внесения под знак дифференциала а) б) в) г) д) 8.1.3. Проинтегрировать по частям а) б) в) г) 8.1.4. Проинтегрировать дроби а) б) 8.2.1. Взять определенные интегралы
и) 8.2.2. Вычислить методом подстановки
8.2.3. Вычислить с помощью универсальной тригонометрической подстановки
8.2.4. Вычислить интегрированием по частям
9.2.1. Разложить в ряд Маклорена
9.2.2. Разложить в ряд Тейлора
9.2.3. Вычислить, взяв три члена соответствующего ряда Маклорена и оценить погрешность ε
9.2.4. Разложить функцию в ряд Фурье периодическую (с периодом Т = 2π) функцию f(x), заданную на отрезке [-π; π]. Постройте график данной функции при
10.1.1. Доказать, что решением дифференциального уравнения y´´´ = 10.1.2. Доказать, что функция y = 10.1.3. Установить, является ли функция x² − y² − Cx = 0 общим интегралом дифференциального уравнения 2xyy´ + x² − y² = 0. 10.1.4. Показать, что функция y = x² + C является решением дифференциального уравнения y´ = 2x. Построить семейство интегральных кривых и выделить интегральную кривую, проходящую через точку (2; 3). 10.1.5. Решить дифференциальное уравнение с разделяющимися переменными, найти частное решение
9.1.1. Найти а) б) в)
9.1.2. Исследовать сходимость ряда, используя следствие из необходимого признака сходимости
9.1.3. Исследовать сходимость ряда с помощью признаков сравнения
9.1.4. Исследовать сходимость ряда с помощью признака Даламбера.
9.1.5. Исследовать сходимость ряда по признаку Коши.
9.1.6. Исследовать сходимость ряда с помощью интегрального признака
9.1.7. Выяснить, сходится ряд абсолютно или условно
10.2.1. Проинтегрировать дифференциальное уравнение y´´ = 10.2.2. Проинтегрировать дифференциальные уравнения, найти указанные частные решения и построить их. а) y´ = б) y´´ = 2; y(0) = 1; y´(0) = − 2; в) y´´´ = 6; y(0) = 1; y´(0) = 3; y´´(0) = 6.
Рефераты
Темы рефератов
1. Особые решения дифференциальных уравнений. 2. Ряд Фибоначчи и его приложения. 3. Золотое сечение. 4. Ряд и интеграл Фурье. 5. Математика и жизнь. 6. Дифференциальные уравнения и их приложения. 7. Кратные интегралы и их приложения. 8. Математика и музыка. 9. Интуиция и математика. 10. Приложения рядов к приближенным вычислениям. 11. Причины введения в математику элементов математического анализа. 12. Комплексные числа и жизнь. 13. История введения комплексных чисел. 14. Нужна ли нам теория вероятностей? 15. Статистика как раздел математики. 16. Теория игр. 17. Фракталы и их приложения. 18. Бифуркации и их значения. 19. Несобственные кратные интегралы. 20. Интегралы Коши, Римана, Лебега. 21. Параметрические интегралы. 22. Диофантов язык и десятая проблема Гильберта. 23. Продуктивность и креативность в математике. 24. Конструктивная математика. 25. Топологические пространства.
Требования к оформлению реферата
Объём реферата 20 страниц машинописного текста, шрифт Times New Roman 14, интервал 1,5, выравнивание по ширине, сквозная нумерация страниц, сквозная нумерация рисунков, сквозная нумерация формул, обязательно список литературы – минимум три источника.
МИНИСТЕРСТВО КУЛЬТУРЫ, СПОРТА И МОЛОДЕЖИ ГОУК ЛНР «ЛУГАНСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ РЕФЕРАТ
Иванов а Иванн а Иванов ича
Преподаватель: Ищенко Н. С. «______»__________20_____г. ___________________________ (подпись)
Студент ____________________________ (Ф.И.О., подпись) «______» ____________ 20____ г.
Луганск 202_ Вопросы к экзамену 1. Понятие числовой последовательности и ее предела. 2. Общие свойства сходящихся последовательностей. 3. Бесконечно малые и бесконечно большие последовательности. 4. Существование предела монотонной ограниченной последовательности. 5. Предельный переход при арифметических операциях над пределами. 6. Число е, натуральные логарифмы. 7. Определение предела функции в точке. 8. Односторонние пределы функции одной переменной. 9. Бесконечно малые и бесконечно большие функции, их сравнение. 10. Свойства сходящихся в точке функций: ограниченность функции в окрестности точки схождения, действия над сходящимися функциями. 11. Эквивалентные функции, их использование при определении предела отношения функций. 12. Первый и второй замечательные пределы. 13. Таблица важнейших пределов. 14. Определение пределов степенно-показательных функций. 15. Непрерывность функции. 16. Определение и классификация точек разрыва. 17. Кусочно-непрерывные функции. 18. Дифференциальное исчисление функций одной переменной 19. Понятие производной функции, геометрический смысл производной. 20. Таблица производных. 21. Основные методы вычисления производных. 22. Производная сложной и неявной функции. 23. Дифференциал функции. 24. Производные высших порядков. 25. Понятие неопределенных выражений. 26. Раскрытие неопределенностей. 27. Правило Лопиталя для раскрытия неопределенностей. 28. Формула Тейлора. 29. Признаки возрастания и убывания функции. 30. Точки локального экстремума. 31. Достаточные условия экстремума функции, выражающиеся через первую и вторую производные функции. 32. Наибольшее и наименьшее значения функции на промежутке. 33. Выпуклость кривой. 34. Точки перегиба. 35. Асимптоты графика функции и их определение. 36. Общая схема исследования функции и построение ее графика. 37. Понятие функции нескольких переменных. 38. Частные производные и техника дифференцирования функции двух независимых переменных. 39. Дифференциал функции. 40. Производная по направлению. 41. Градиент функции. 42. Понятие об эмпирических формулах. 43. Метод наименьших квадратов (МНК). 44. Понятие условного экстремума функции многих переменных. 45. Метод неопределенных множителей Лагранжа решения задач на условный экстремум. 46. Понятие первообразной функции и неопределенного интеграла. 47. Свойства неопределенного интеграла. 48. Табличные интегралы. 49. Методы интегрирования: заменой переменных, по частям. 50. Линейность интегрирования. 51. Интегрирование рациональных, иррациональных и тригонометрических функций, рационализирующие подстановки. 52. Определение определенного интеграла. 53. Геометрический смысл определенного интеграла. 54. Формула Ньютона-Лейбница. 55. Свойства определенного интеграла: перестановка границ интегрирования, аддитивность относительно границ интегрирования, линейность интегрирования. 56. Интегрирование заменой переменной и по частям в определенном интеграле. 57. Решение геометрических задач с помощью определенных интегралов. 58. Понятие о несобственных интегралах. 59. Интеграл по бесконечному промежутку. 60. Понятия о кратных интегралах. 61. Определение кратного интеграла. 62. Свойства кратного интеграла и интегрирование функций многих переменных. 63. Приведение кратного интеграла к повторным интегралам. 64. Понятие о несобственных интегралах. 65. Интеграл по бесконечному промежутку. 66. Понятия о кратных интегралах. 67. Определение кратного интеграла. 68. Свойства кратного интеграла и интегрирование функций многих переменных. 69. Приведение кратного интеграла к повторным интегралам. 70. Определение числового ряда и его суммы. 71. Прогрессии. 72. Необходимое условия сходимости, критерий Коши сходимости числового ряда. 73. Гармонический ряд, его расходимость. 74. Достаточные условия сходимости рядов с положительными членами. 75. Признак Даламбера. 76. Радикальный интегральный признак Коши. 77. Знакопеременные числовые ряды, абсолютная и условная сходимость. 78. Знакочередующиеся ряды, признак сходимости. 79. Понятие функциональной последовательности и функционального ярда. 80. Определение степенного ряда, теорема Абеля о его сходимости. 81. Радиус и интервал сходимости сходящегося степенного ряда, формулы вычисления. 82. Ряды и элементарные функции. 83. Ряд Маклорена. 84. Некоторые применения степенных рядов. 85. Обычное дифференциальное уравнение первого порядка, задача Коши. 86. Теорема о существовании и единственности решения дифференциального уравнения первого порядка. 87. Частное и общее решение. 88. Уравнения с разделенными и разделяющимися переменными. 89. Дифференциальные уравнения, сводимые к уравнениям с разделяющимися переменными. 90. Линейные дифференциальные уравнения первого порядка. 91. Понятие дифференциального уравнения 2-го порядка и его частного и общего решения. 92. Линейное дифференциальное уравнение второго порядка: общее и частное решение. 93. Решение линейных дифференциальных уравнений второго порядка с постоянными коэффициентами. Основная литература
1. Агарева, О. Ю. Математическая логика и теория алгоритмов: учеб. пособие / О. Ю. Агарева, Ю. В. Селиванов. – М.: МАТИ, 2011. – 80 с. 2. Баврин, И. И. Курс высшей математики: учебник / И. И. Баврин. –2-е изд., перераб. и доп. –М.: ВЛАДОС, 2004. –561 с. 3. Берман, Г. Н. Сборник зада по курсу математического анализа: учеб. пособие / Г. Н. Берман. –СПб: Лань, 2016. – 492 с. 4. Воронкін, О. С. Вища математика: Методичні вказівки та індивідуальні завдання з дисципліни “Вища математика” для студентів спеціалізації 6.020204 “Звукорежисура” усіх форм навчання / О. С. Воронкін, П. С. Солодовник. –Луганськ: ЛДАКМ, 2013. –75 с. 5. Выгодский, М. Я. Справочник по высшей математике / М. Я. Выгодский. – М.: АСТ: Астрель, 2006. – 991 с. 6. Высшая математика для экономистов: учебник для вузов / Н. Ш. Кремер, Б. А. Путко, И. М. Тришин и др. –2-е изд., перераб. и доп. –М.: ЮНИТИ, 2004. –471 с. 7. Высшая математика. Практикум, Ч. 1 / А. В. Конюх, С. В. Майоровская, О. Н. Поддубная, В. А. Рабцевич. –Минск: [б. и.], 2014. –274 с. 8. Высшая математика: учеб. пособие / Г. Л. Луканкин и др.; под ред. Г. Н. Яковлева. –М.: Просвещение, 1988. –431 с. 9. Гусак, А. А. Основы высшей математики: пособие для студ. вузов / А. А. Гусак, Е. А. Бричкова. – Минск: ТетраСистемс, 2012. –208 с. 10. Данко, П. Е. Высшая математика в упражнениях и задачах. В. 2 ч.: учеб. пособие, Ч. 1 / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова. –6-е изд. –М.: ОНИКС 21 век, 2003. 11. Данко. П. Е. Высшая математика в упражнениях и задачах. В. 2 ч.: учеб. пособие, Ч. 2 / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова. –6-е изд. –М.: ОНИКС 21 век, 2003. – 416 с. 12. Деменева, Н. В. Комплексные числа: учебное пособие / Н. В. Деменева. – Пермь: Прокростъ, 2017. – 112 с. 13. Демидович, В. П. Краткий курс высшей математики: учеб. пособие / Б. П. Демидович, В. А. Кудрявцев. –М.: АСТ, 2001. –656 с. 14. Епихин, В. Е. Комплексные числа: метод. разработка / В. Е. Епихин. –М.: МГУ, 2008. –16 с. 15. Зюзьков, В. М. Математическая логика и теория алгоритмов: учебное пособие / В. М. Зюзьков. – Томск: Эль Контент, 2015. – 236 с. 16. Кастрица, О. А. Высшая математика: примеры, задачи, упражнения: учеб. пособие для вузов / О. А. Кастрица. – М.: ЮНИТИДАНА, 2002. – 543 с. 17. Клименко Ю. И. Высшая математика для экономистов: теория, примеры, задачи: учебник / Ю. И. Клименко. –М.: Экзамен, 2005. –736 с. 18. Красс, М. С. Математика для экономических специальностей / М. С. Красс, Б. П. Чупрынов. –СПб.: Питер, 2005. –464 с. 19. Краткий курс высшей математики: учебник / под общ. ред. проф. К. В. Балдина. –2-е изд. –М.: Дашков и К, 2015. –510 с. 20. Кундышева, Е. С. Математика: учебник / Е. С. Кундышева. – Москва: Дашков и Кº, 2011. – 561 с. 21. Литова, Г. Г. Основы векторной алгебры: учеб.-метод.пособие / Г. Г. Литова, Д. Ю. Ханукаева. –М.: РГУ нефти и газа им. И. М. Губкина, 2009. – 90 с. 22. Малыхин, В. И. Высшая математика: учебное пособие / В. И. Малыхин. – М.: Инфра-М, 2009. –365 с. 23. Натансон, Н. П. Краткий курс высшей математики/ Н. П. Натансон. – СПб.: Лань, 2001. – 736 с. 24. Общий курс высшей математики для экономистов:: учебник / под ред. В. И. Ермакова. –М.: Инфра-М, 1999. –656 с. 25. Пискунов, Н. С. Дифференциальные и интегральные исчисления: учеб. пособие для втузов. Т. 1 / Н. С. Пискунов. –13-е изд. –М.: Наука, 1985. –432 с. 26. Пискунов, Н. С. Дифференциальные и интегральные исчисления: учеб. пособие для втузов. Т. 2 / Н. С. Пискунов. –13-е изд. –М.: Наука, 1985. –560 с. 27. Умнов, А. Е. Аналитическая геометрия и линейная алгебра: учеб. пособие / А. Е. Умнов. –3-е изд., испр. и доп. –М.: МФТИ, 2011. –544 с. 28. Фихтенгольц, Г. М. Курс дифференциальные уравнения и операционное исчисление. Т. 1 / Г. М. Фихтенгольц. –Изд. 5-е, стереотип. –М.: ГИФМЛ, 1962. –607 с. 29. Шилкина, Е. И. Высшая математика: Часть 2. Учеб.-практ. пособие / Е. И. Шилкина, М. П. Дымков, В. А. Рабцевич. – Мн.: БГЭУ, 2014. – 167 с. 30. Шипачев, В. С. Основы высшей математики: учебное пособие для вузов / В. С. Шипачев; под ред. А. Н. Тихонова. –М.: Высшая школа, 1994. – 479 с.
Высшая математика, МЗР-1
Содержание дисциплины
РАЗДЕЛ 5. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ (II СЕМЕСТР)
|
||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 160; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.250.143 (0.014 с.) |

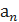 =
= 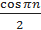 .
.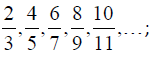
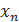 , если
, если  =
= 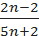 , a =
, a = 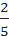 .
.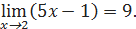
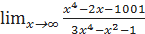 ;
;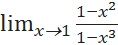 ;
;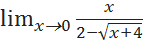 ;
;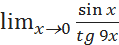 ;
;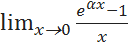 .
.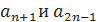 члены ряда:
члены ряда: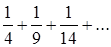 ;
; 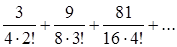 ;
; 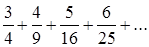
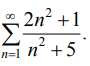
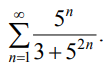
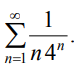
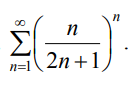
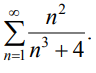
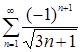
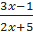 .
.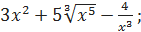
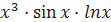 ;
;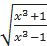 .
.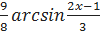 .
.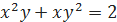 .
.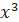 ·lnx.
·lnx.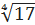 с точностью до двух знаков после запятой.
с точностью до двух знаков после запятой.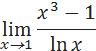
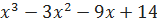 .
.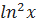 .
.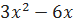 на отрезке
на отрезке 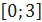 .
.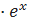 .
.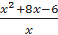 .
.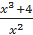 и построить ее график.
и построить ее график.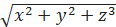 – x·y·z в точке М(2; –2; 1).
– x·y·z в точке М(2; –2; 1).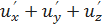 в точке
в точке 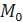 (1, 1, 1), если u = ln(1 + x +
(1, 1, 1), если u = ln(1 + x + 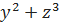 ).
).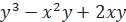 , точка
, точка 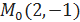 и вектор
и вектор 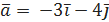 . Требуется найти производную функцию z в точке
. Требуется найти производную функцию z в точке 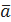 и градиент функции в данной точке.
и градиент функции в данной точке.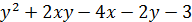 .
.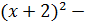
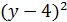 , если ее аргументы связаны уравнением x + 3y = 0.
, если ее аргументы связаны уравнением x + 3y = 0.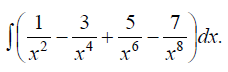
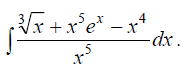
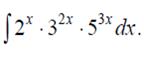
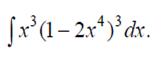
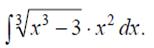
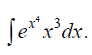
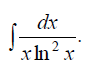
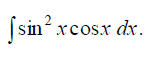
 ;
;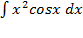 ;
;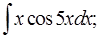
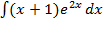 .
.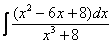
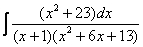
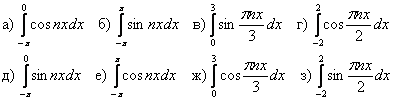
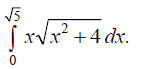
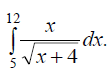
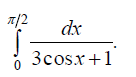
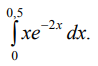
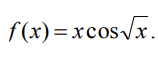

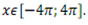
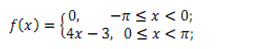
 является функция y = − sin x + 2x + C.
является функция y = − sin x + 2x + C.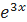 является решением дифференциального уравнения y´´´ − 3y´ − 18y = 0.
является решением дифференциального уравнения y´´´ − 3y´ − 18y = 0.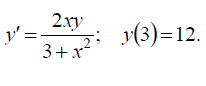
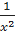 . Найти частное решение, удовлетворяющее начальным условиям: y(1) = 0, y´(1) = 1.
. Найти частное решение, удовлетворяющее начальным условиям: y(1) = 0, y´(1) = 1.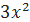 ; y(0) = 2;
; y(0) = 2;


