
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные формулы комбинаторикиСодержание книги Поиск на нашем сайте
Комбинаторика – раздел математики, изучающий вопросы о том, сколько комбинаций определённого типа можно составить из данных предметов (элементов). Определение 1. Размещениями из n различных элементов по m элементов ( Пример. Из трёх элементов a, b, c можно составить следующие размещения по два элемента: ab, ac, bc, ba, ca, cb. Число различных размещений без повторений из n элементов по m элементов определяется по формуле:
Размещения с повторениями (n различных элементов, элементы могут повторяться):
Пример. Возьмем буквы Б, А, Р. Какие размещения из этих букв, взятых по две, можно получить? Сколько таких наборов получиться, если: 1) буквы в наборе не повторяются; 2) буквы могут повторяться? 1) Получатся следующие наборы: БА, БР, АР, АБ, РБ, РА.
2) Получатся наборы: ББ, БА, БР, АА, АБ, АР, РР, РБ, РА.
Определение 2. Перестановками из n различных элементов называют размещения из этих n элементов по n. Перестановки можно считать частным случаем размещений при m= n. Тогда число всех перестановок без повторений из n элементов вычисляется по формуле:
Перестановки с повторениями (k различных элементов, где элементы могут повторяться
Пример. Возьмем буквы Б, А, Р. Какие перестановки из этих букв можно получить? Сколько таких наборов получится, если: 1) буквы в наборе не повторяются; 2) буква А повторяется два раза? 1) Получатся наборы: БАР, БРА, АРБ, АБР, РАБ, РБА.
2) Получатся наборы: БАРА, БРАА, БААР, ААРБ, ААБР, АБАР, АРАБ, АРБА, АБРА, РАБА, РААБ, РБАА.
Определение 3. Сочетаниями из n различных элементов по m элементов называются комбинации, составленные из данных n элементов по m элементов, которые отличаются хотя бы одним элементом. Отметим разницу между сочетаниями и размещениями: в первых не учитывается порядок элементов. Число сочетаний без повторений из n различных элементов по m элементов вычисляется по формуле:
Пример. В лабораторной клетке содержат трёх белых и трёх коричневых мышей. Найдите число способов выбора двух мышей, если они могут быть любого цвета. m=2, n =6, тогда Сочетания с повторениями (n элементов, взятых по m, где элементы могут повторяться):
Пример. Возьмем плоды: банан (Б), ананас (А) и репа(Р).Какие сочетания из этих плодов, взятых по два, можно получить? Сколько таких наборов получится, если: 1) плоды в наборе не повторяются; 2) можно брать по два одинаковых плода? 1) Получатся наборы: БА («банан, ананас» и «ананас, банан» – один и тот же набор), АР и РБ.
2) Получатся наборы: ББ, БА, БР, АА, АР, РР.
Задачи 1. В ящике 15 белых, 12 красных и 14 синих шаров. Вынули один шар. Определить вероятность того, что вынутый шар красный. 2. В денежно-вещевой лотерее на серию из 1000 билетов приходится 3 денежных и 8 вещевых выигрышей. Какова вероятность какого-либо выигрыша на один лотерейный билет? 3. Бросается один раз игральная кость. Какова вероятность того, что выпадет 1 или 5 очков? 4. В ящике 8 белых и 4 синих шара. Вынули сразу 2 шара. Определить вероятность того, что все шары синие? 5. В коробке 20 ламп - 18 исправных и 2 бракованных. Из коробки вынимают 3 лампы. Какова вероятность того, что все они исправные? 6. Бросается один раз игральная кость. Какова вероятность того, что выпадет 1 или 5 очков? 7. Сколько различных слов можно получить перестановками всех букв в слове ЖУК? 8. Сколько различных слов можно получить перестановками всех букв в слове МАТЕМАТИКА? 9. Сколькими способами из 5 шаров можно выбрать 2? 10. Сколькими способами из 10 студентов можно выбрать 3 делегатов на конференцию? Свойства вероятности
|
||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 202; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.123.41 (0.008 с.) |

 ) называют комбинации, составленные из данных n элементов по m элементов, которые отличаются либо самими элементами, либо порядком элементов.
) называют комбинации, составленные из данных n элементов по m элементов, которые отличаются либо самими элементами, либо порядком элементов.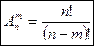 .
. .
.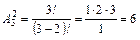 .
.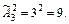
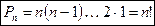
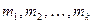 раз и
раз и 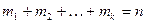 , где n – общее количество элементов):
, где n – общее количество элементов):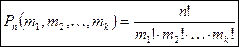 .
.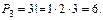

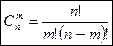 .
.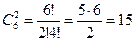 .
.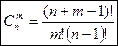 .
. .
.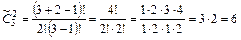 .
.


