
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Устойчивость сжатых стержней
Упругие сжатые стержни в зависимости сжимающих напряжений могут оказаться в устойчивом, неустойчивом и безразличном состоянии равновесия. Если сжатый стержень после снятия дополнительного внешнего воздействия, вызвавшего отклонение прямолинейного стержня от исходного положения, возвратится в первоначальное неискривленное состояние, то такое состояние стержня называется устойчивым. Устойчивое состояние равновесия стержня – это состояние сжатого стержня, сохраняющее его первоначальную геометрическую форму, после устранения причины, отклонившей его из этого состояния, называется устойчивым. Если после снятия дополнительного воздействия стержень остается в деформированном слегка изогнутом состоянии, т.е. не возвращается в исходное состояния, то его состояние неустойчивое по отношению в первоначальному неискривленному состоянию. Неустойчивое состояние равновесия стержня – это состояние сжатого стержня, не охраняющее его первоначальную геометрическую форму, после устранения причины, отклонившей его из этого состояния, называется неустойчивым. Если при этом изогнутый стержень вернуть в первоначальное неизогнутое состояние, то он и в этом состоянии будет находиться в равновесии, т.е. при такой нагрузке наблюдается раздвоение форм равновесия и неискривленная форма может перейти в искривленную. Прямолинейная форма становится неустойчивой. Прямолинейная форма равновесия будет устойчивой только в том случае, когда сжимающая сила меньше некоторого определенного значения, которое называется критическим. Критическая сила сжатого стержня - нагрузка, под действием которой стержень может находиться в безразличном состоянии равновесия. Теоретически критических сил может быть бесконечное множество, если прочность материала неограниченна. Однако практическое значение имеет, главным образом, первая наименьшая критическая сила, под действием которой стержень может находиться в равновесии как в прямолинейном, так и в слегка изогнутом состоянии, что соответствует потере устойчивости стержня. Потеря устойчивости сжатого стержня - это изменение первоначальной прямолинейной формы равновесия сжатого стержня. Критическое состояние и критическую нагрузку следует считать разрушающими, так как в этом состоянии к напряжениям сжатия добавляются изгибные напряжения, которые могут оказаться большими даже при небольших искривлениях стержня и стержень может разрушиться. Разрушающая нагрузка при потере устойчивости стержня - это сжимающая нагрузка, равная критической силе.
Для вычисления перемещений в стержне при потере устойчивости прямолинейной формы нужно исходить из точного дифференциального уравнения изогнутой оси
но для вычисления значения критической силы достаточно использовать приближенное дифференциальное уравнение, когда влиянием углов поворота
Формула Эйлера
Для вывода формулы критической силы (формулы Эйлера) рассматривается сжатый стержень в безразличном слегка изогнутом состоянии. Безразличное состояние равновесия стержня, возникающее при критической силе – это такое состояние, когда сжатый стержень может сохранять прямолинейную недеформированную или слегка изогнутую форму. Используем приближенное дифференциальное уравнение изогнутой оси стержня Однако этот процесс можно сократить, если использовать уже подготовленное уравнение изогнутой оси стержня в начальных параметрах. Остается лишь подчинить это уравнение условиям закрепления стержня на опорах. Это условия, отвечающие определенным известным значениям силовых или деформационных параметров на концах стержня. Из этих условий можно получить систему однородных уравнений, определитель которой приравнивается нулю. Такая система уравнений, описывающих условия закрепления стержня на опорах, однородная, т.е. правая часть равна нулю. В тривиальном решении неизвестные силовые и деформационные факторы будут равны нулю, что не отвечает потере устойчивости, т.е. потере первоначальной прямолинейной формы равновесия. Чтобы получить ненулевое решение нужно главный определитель приравнять нулю. При этом числитель и знаменатель при определении неизвестных параметров будут равны нулю, что дает неопределенное, но ненулевое решение.
Такой определитель приводится к трансцендентному уравнению. Трансцендентное уравнение имеет вид уравнения не представляющего алгебраические функции из букв и цифр, связанных алгебраическими действиями. Собственные числа этого уравнения позволяют найти параметр k, а затем по (11.2) найти критическую силу Собственные числа - это корни трансцендентного уравнения, при которых функция принимает нулевое значение.
Согласно (11.6) уравнение изогнутой оси стержня принимает вид
В этом уравнении остается один неизвестный начальный параметр θ0 (кроме уже использованных), соответственно чему осталось одно граничное условие при z = l y =0.Обратим внимание на то, что здесь нельзя брать условие симметрии изогнутого стержня, так как при этом останутся неучтенными кососимметричные формы изгиба стержня. Таким образом, из условия шарнирного закрепления стержня на правой опоре находим, что
и уравнение изогнутой оси
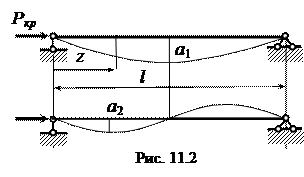
При n =1 получаем наименьшее значение критической силы
которой соответствует изгиб стержня по синусоиде с одной полуволной (рис. 11.2). При n =2 критическая сила в четыре раза больше первой, а стержень изгибается по синусоиде с двумя полуволнами. Так можно получить бесконечное множество критических состояний. Но изгиб стержня по синусоиде с n -ным количеством полуволн (минуя предшествующие) может произойти при особах условиях загружения (например, при воздействии взрывной волны), а при статическом нагружении каждой последовательно возрастающей критической силе соответствует n -ное и (n -1)-е состояние равновесия. Так, при первой критической силе возможны прямолинейная форма равновесия и форма изгиба по одной полуволне. Поскольку при незначительном превышении критической силы происходит стремительное возрастание прогибов, когда возникают большие изгибные напряжения, то в инженерной практике для сжатых стержней критическую силу (даже первую) допускать нельзя. Поэтому за критическую принимают первую наименьшую силу, которую считают разрушающей. По этой силе устанавливается пас устойчивости сжатого стержня.
Поскольку в этом уравнении два неизвестных параметра y 0 и θ0, то нужно рассмотреть два условия при z = l y = θ = 0. Из этих условий получим два однородных уравнения:
Чтобы иметь ненулевые значения начальных параметров y 0 и θ0 , определитель этой системы приравниваем нулю. Отсюда получаем
По уравнению изогнутой оси из условия z = l y =0 находим Здесь и дальше ограничимся только первой критической силой и ей соответствующего уравнения изогнутой оси.
Если на верхнем конце стержня установить шарнирную опору (рис. 11.3 б), то согласно 11.6 получим:
Здесь наличие реакции А очевидно из суммы моментов всех сил относительно заделки, где возникает опорный момент, а направление ее может быть какое угодно (как влево, так и вправо). Из условия защемления на нижнем конце стержня при z = l y =θ=0 получаем систему уравнений
определитель которой приравниваем нулю:
Отсюда получаем трансцендентное уравнение
На основании уравнения изогнутой оси стержня (11.9) из условия, при z = l y =0, можно выразить θ0 через А. Тогда уравнение изогнутой оси стержня (11.9) примет следующий вид: Положение сечения с наибольшим прогибом найдем, приравнивая угол поворота Рассмотрим стержень, жестко защемленный с двух сторон (рис. 11.3 в), при чем верхняя заделка является вертикально подвижной. Согласно (11.6) получаем:
Из условия при z = l y =θ=0 получаем систему однородных уравнений, определитель которой приравниваем нулю:
Отсюда получаем трансцендентное уравнение
Все формулы критической силы при различных условиях закрепления можно представить в виде
где μ – коэффициент приведения длины, указывающий, какая часть действительной длины стержня изгибается по синусоиде с одной полуволной аналогично основному случаю (рис.11.2). Поскольку
Знаменатель этой формулы для каждого конкретного случая находится из трансцендентного уравнения. Если это уравнение дает несколько корней, то для вычисления наименьшей критической силы нужно брать наименьший корень kl, чтобы коэффициент приведения длины (11.13) был наибольшим, а критическая сила наименьшей. Один из корней уравнения (11.12) получим, положив
На основании уравнения изогнутой оси (11.12) из условия защемления, т.е. при z = l y =0, можно выразить М 0 через А, и тогда уравнение изогнутой оси стержня примет следующий вид
Вторая критическая сила с коэффициентом приведения длины μ=0,35 соответствует кососимметричной форме изгиба и проявляется она после первой формы, что практического значения не имеет. В случае свободно смещающейся заделки (рис. 11.4 г) уравнения изогнутой оси и углов поворота имеют следующий вид:
Из условий
|
||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 101; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.129.100 (0.02 с.) |
 ,
,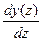 пренебрегают.
пренебрегают.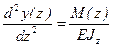 , а его решение подчиним условиям закрепления стержня на опорах.
, а его решение подчиним условиям закрепления стержня на опорах.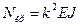 .
. Рассмотрим простейший случай стержня шарнирно закрепленного на опорах (основной случай), рис. 11.2. В этом случае на опоре (при z =0)
Рассмотрим простейший случай стержня шарнирно закрепленного на опорах (основной случай), рис. 11.2. В этом случае на опоре (при z =0) 
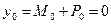 .
.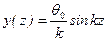 .
.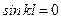 . Это значит, что
. Это значит, что  , а, следовательно, из (11.2) найдем критическую силу
, а, следовательно, из (11.2) найдем критическую силу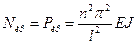 , n = 1, 2, 3,
, n = 1, 2, 3, 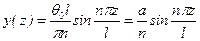 .
.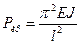 , (11.7)
, (11.7)
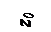
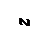
 Если стержень жестко защемлен с одной стороны, а с другой свободный (рис.11.3, а), то при выборе начала координат на свободнном конце стержня
Если стержень жестко защемлен с одной стороны, а с другой свободный (рис.11.3, а), то при выборе начала координат на свободнном конце стержня  . Следовательно, согласно (11.6) получим
. Следовательно, согласно (11.6) получим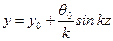 .
.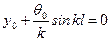 ,
,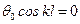 .
.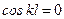 , т.е.
, т.е. 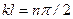 , n =1, 3, … Следовательно, критическая сила и уравнение изогнутой оси стержня будут следующими:
, n =1, 3, … Следовательно, критическая сила и уравнение изогнутой оси стержня будут следующими: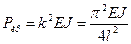 , (11.8)
, (11.8)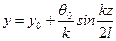 .
.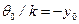 , Следовательно,
, Следовательно, 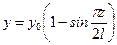 , что соответствует форме изгиба, показанной на рис. 11.3 а.
, что соответствует форме изгиба, показанной на рис. 11.3 а.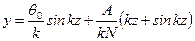 , (11.9)
, (11.9)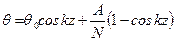 .
.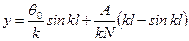 , (11.10)
, (11.10)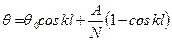 ,
,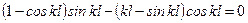 .
.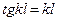 , откуда находим первый корень
, откуда находим первый корень 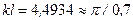 . Значит, согласно (11.2)
. Значит, согласно (11.2)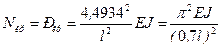 . (11.11)
. (11.11)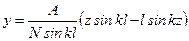 .
.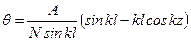 нулю. Из этих условий найдем
нулю. Из этих условий найдем 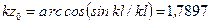 , т.е. z 0=0,3983 l. В этом сечении возникает прогиб
, т.е. z 0=0,3983 l. В этом сечении возникает прогиб  . Точка перегиба на изогнутой оси будет там, где кривизна
. Точка перегиба на изогнутой оси будет там, где кривизна 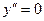 , т.е. при
, т.е. при 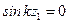 . Отсюда находим длину участка стержня до точки перегиба z 1 =0,7 l.
. Отсюда находим длину участка стержня до точки перегиба z 1 =0,7 l.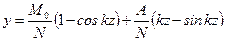 , (11.12)
, (11.12)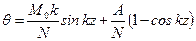 .
.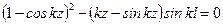 .
.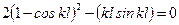 или
или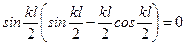 . (11.13)
. (11.13)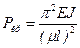 , (11.14)
, (11.14)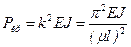 , то коэффициент приведения длины можно находить по формуле
, то коэффициент приведения длины можно находить по формуле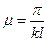 . (11.15)
. (11.15)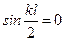 , что соответствует значению
, что соответствует значению 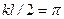 . Второй корень найдем, положив
. Второй корень найдем, положив  , откуда находим
, откуда находим 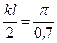 . По меньшему значению корня kl =2π определяем коэффициент приведения длины μ=0,5, чему соответствует критическая сила
. По меньшему значению корня kl =2π определяем коэффициент приведения длины μ=0,5, чему соответствует критическая сила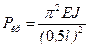 . (11.16)
. (11.16)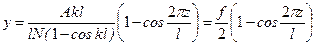 .
.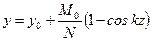 ,
, 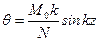 .
.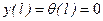 получим kl =π, т.е. μ=1. Критическая сила такая же, как в основном случае.
получим kl =π, т.е. μ=1. Критическая сила такая же, как в основном случае.


