
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изгиб с кручением. Расчет круглого вала
Одновременное действие изгиба с кручением не является характерным случаем сложного сопротивления для строительных конструкций. Это более типично для различных деталей машин, например: коленчатый вал, который воспринимает крутящий момент в сочетании с изгибом, или оси моторных вагонов и т.д. Совместное действие изгиба и кручения является наиболее характерным случаем загружения круглого вала. Рассмотрим вал, подвергающийся изгибу в 2-х плоскостях под воздействием сил Рх и Ру, и кручению под воздействием крутящего момента Мкр. Под действием указанных нагрузок в опасном сечении вала возникнут (рис. 10.11): - нормальные напряжения от изгиба в вертикальной и горизонтальной плоскости: σz(Mx) = - касательные напряжения: τкр(M кр) Для упрощения анализа рассматриваемого воздействия и в силу симметричности рассматриваемого сечения относительно осей х и у (Wx = Wy = W и момент сопротивления при изгибе). Определим максимальные нормальные напряжения от действия результирующего изгибающего момента Мр σmax =
Определим эквивалентный расчетный момент по III теории прочности:
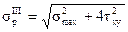
Учитывая, что Wx = Wy = W = W ρ / 2 получим:
Аналогично по IV теории прочности с учетом необходимых преобразований найдем
Далее условие прочности можно записать, как σрасч =
отсюда W тр ≥ а диаметр вала
МОДУЛЬ 11. ПРОДОЛЬНО-ПОПЕРЕЧНЫЙ ИЗГИБ И УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ
Продольно-поперечный изгиб
Из самого названия напряженно-деформированного состояния следует, что стержень загружен не только поперечной, но и продольной нагрузкой, рис. 11.1.
Следовательно, продольно-поперечный изгиб – это вид деформации, когда на стержень одновременно действует продольная и поперечная нагрузка. Поперечная нагрузка вызывает изгиб стержня, а продольная – в основном сжатие. Можно ли в этом случае вычислять напряжения по принципу суперпозиции
В случае весьма жестких стержней напряжения, вычисленные по формуле (11.1), будут достаточно достоверными, но в случае гибких стержней (с небольшой изгибной жестокостью) применение формулы (11.1) приведет к большой погрешности. Принцип суперпозиции при продольно-поперечном изгибе не применим, так как продольная сила Для вычисления действительных напряжений дополнительный изгибающий момент нужно вычислять с учетам действительных прогибов, вызванных одновременный воздействием как поперечной так и продольной нагрузок. Задача сводится к вычислению этих перемещений, т.е. к определению уравнения изогнутой оси стержня. Наиболее эффективно при этом использовать метод начальных параметров. Рассмотрим балку под действием продольной силы
Обозначив через
получим
Решение этого уравнения представим в виде
Разыскивая частное решение y * в виде полинома y *= a + bz и подставляя его в исходное уравнение (11.3), способом неопределенных коэффициентов находим
При этом уравнение (11.3) примет следующий вид
Отсюда дифференцированием можно получить уравнение углов поворота
Выразим постоянные интегрирования А и В через начальные параметры из условий, что при z =0, y = y 0,
Если бы к балке была приложена только сила P 0, то уравнение изогнутой оси (11.3) имело бы вид
В случае загружения балки лишь одним моментом M 0
Здесь
Отсюда следует, что к поперечной нагрузке можно применять принцип суперпозиции, но при каждом загружении нужно учитывать продольную силу.
|
||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 154; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.238.76 (0.007 с.) |
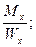 σz(My) =
σz(My) = 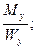
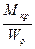 .
. (10.16)
(10.16)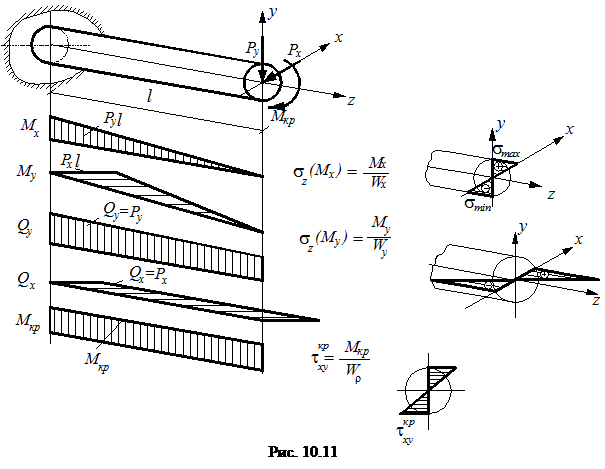
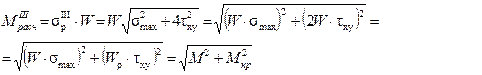 (10.17)
(10.17)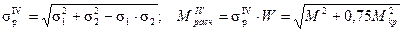 (10.18)
(10.18)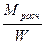 ≤ R (10.19)
≤ R (10.19)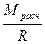
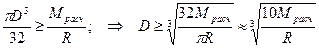 (10.20)
(10.20)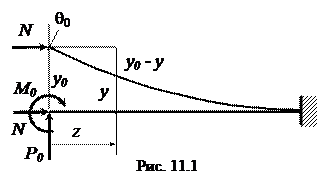
 (11.1)
(11.1)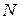 в изогнутом стержне вызывает дополнительный изгиб Принцип суперпозиции – принцип независимости и сложения действия сил, заключающийся в том, что силовые фактор, напряжения и перемещения, т.е. все, кроме работы и потенциальной энергии, можно вычислять от каждой нагрузки отдельно и результаты складывать.
в изогнутом стержне вызывает дополнительный изгиб Принцип суперпозиции – принцип независимости и сложения действия сил, заключающийся в том, что силовые фактор, напряжения и перемещения, т.е. все, кроме работы и потенциальной энергии, можно вычислять от каждой нагрузки отдельно и результаты складывать.
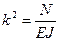 (11.2)
(11.2)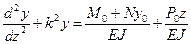 (11.3)
(11.3)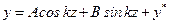
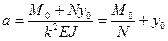 ,
, 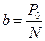 .
.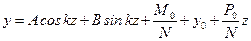 (11.4)
(11.4)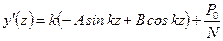 , (11.5)
, (11.5)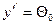 . Из этих условий находим
. Из этих условий находим 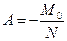 ,
, 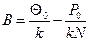 или
или 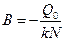 . Подставляя в уравнение (11.5) постоянные А и В, получим
. Подставляя в уравнение (11.5) постоянные А и В, получим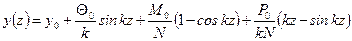 . (11.6)
. (11.6)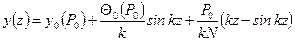 .
.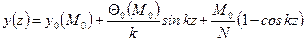 .
.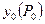 ,
, 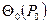 ,
, 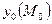 ,
, 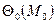 - начальные параметры при отдельном загружении балки нагрузками
- начальные параметры при отдельном загружении балки нагрузками 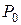 и
и 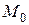 соответственно.
соответственно.


