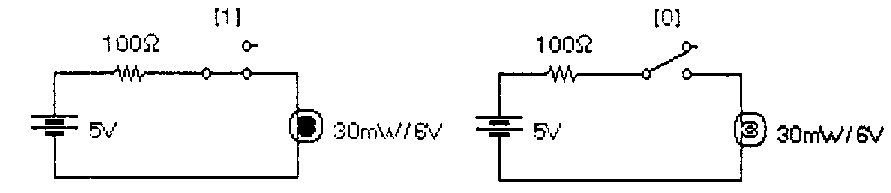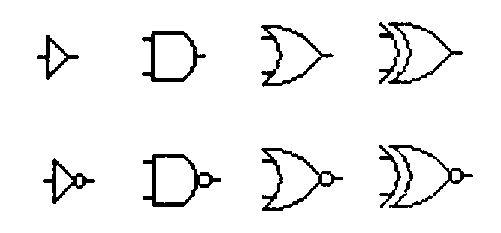Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
М. В. Виноградов, Е. М. СамойловаСодержание книги
Поиск на нашем сайте
МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Саратовский государственный технический университет Имени Гагарина Ю.А.»
М.В.Виноградов, Е.М.Самойлова
ЦИФРОВыЕ системы УПРАВЛЕНИя
Учебное пособие по курсам «Схемотехника систем управления» «Схемотехника микропроцессорных структур» «Системы автоматизации и управления» «Проектирование систем автоматизации и управления» для студентов направлений 15.03.04, 15.04.04
Саратов 2019 УДК 681.5, 681.3 ББК 32.96-04 И 26
Одобрено редакционно-издательским советом Саратовского государственного технического университета имени Гагарина Ю.А.
Виноградов М.В., Самойлова Е.М. И 26 Цифровые системы управления: учеб. пособие / М.В. Виноградов, Е.М. Самойлова, Саратов: Сарат. гос. техн. ун-т, 2019. 120 с. ISBN 978-5-7433-2829-1
Рассматриваются методы и примеры проектирования логических схем, а на их основе и последовательностных цифровых систем управления. Представлены различные аппаратные средства и программное обеспечение для проектирования, моделирования и реализации схем современных цифровых систем управления. Пособие поможет овладеть методами и техникой проектирования не только отдельных логических схем, но и больших функционально законченных систем машиностроительного производства. Пособие предназначено для студентов направлений 15.03.04, 15.04.04 изучающих дисциплины «Схемотехника систем управления», «Схемотехника микропроцессорных структур», «Системы автоматизации и управления» «Проектирование систем автоматизации и управления»
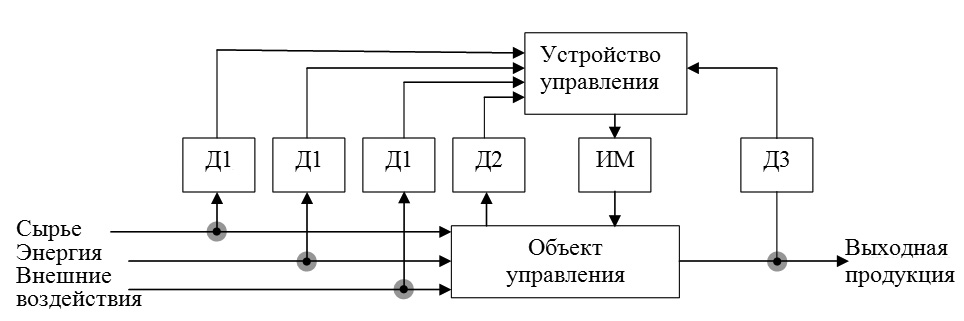
© Саратовский государственный технический университет, 2019 © Виноградов М.В., ISBN 978-5-7433-2829-1 Самойлова Е.М., 2019 ВВЕДЕНИЕ Продолжается чрезвычайно быстрый рост производства средств цифровой техники, которые проникают во все сферы человеческой деятельности – от космических исследований и автоматизации промышленного производства до медицины и повседневного быта в виде автоматизированных и автоматических систем сбора и обработки информации, управления и контроля. Вследствие этого повышается интерес все более широкого круга специалистов самых различных отраслей знаний к цифровой технике, ее потенциальным возможностям. В таких условиях естественно возникает необходимость в пособии по методам и технике проектирования цифровых устройств на базе современных достижений технологии производства средств вычислительной техники, не требующем от читателя специальной подготовки в теории переключательных (логических) функций. Спроектированное устройство минимизируется по количеству элементов для повышения его надежности и снижения стоимости. Одной из задач настоящего пособия является рассмотрение основного этапа разработки цифровых устройств — их логического проектирования на базе современных интегральных схем. Это поможет овладеть методами и техникой проектирования не только отдельных логических схем, но и больших функционально законченных систем. Рассмотрены также варианты проектирования асинхронных последовательностных схем. Отличительной особенностью логического проектирования является использование теоретических положений Булевой алгебры, графов переходов и техники моделирования схем с использованием программ Electronics Workbench (EWB) и OWEN Logic. С начала 70-х годов прошлого столетия разработчики систем управления имеют принципиально новые технические средства – микропроцессоры для управления и микро – ЭВМ для отладки процесса управления. С их появлением стало возможным привлекать современные средства автоматики и вычислительной техники к решению обычных (не уникальных) технических задач. Современные устройства цифровой электроники проникают во все сферы нашей жизни: электронные часы, электронные замки в подъездах, ЭВМ, ЧПУ и т.д. Основу всех этих устройств составляют цифровые схемы логических цепей, регистров, счетчиков, таймеров, коммутаторов, дешифраторов, сумматоров, преобразователей и т.п. Понимание физических принципов работы этих схем и методов конструирования сложных систем на их основе является необходимым условием надежной работы средств автоматизации. Появление микропроцессорных БИС позволяет уменьшить стоимость микро – ЭВМ, сравнимых по своим параметрам с ранее созданными ЭВМ на 3…4 порядка, габаритные размеры на 4 порядка, потребляемую мощность в 105 раз это дает возможность увеличить при тех же затратах производство ЭВМ в сотни и тысячи раз перевести устройства на базе микропроцессоров из разряда специальных в обыденные: кухонные таймеры, роботы, станки, линии и т.д. Специалист, использующий ЭВМ в своей повседневной деятельности должен иметь правильное представление о ее возможностях и построении. Он должен понимать, каким образом ЭВМ управляет оборудованием, как она собирает и обрабатывает информацию, какие возможности ЭВМ можно использовать для повышения производительности труда. Надо уметь создать схему, обеспечивающую связь ЭВМ с управляемым объектом. Замена дискретных устройств ЧПУ на микропроцессор позволило создать системы, в которых программа меняется без участия человека – оператора. Управление – это процесс воздействия на объект с целью привести его в желаемое состояние или положение (из кибернетики). Объектом управления – называется объект, нуждающийся в специально организованном управляющем воздействии для успешного взаимодействия с другими объектами или внешней средой. Чтобы появилась возможность управлять объектом, необходимо наличие набора правил, позволяющих достигать поставленной цели управления в различных ситуациях, т.е. алгоритма управления и устройства управления – способного создавать управляющее воздействие в соответствии с алгоритмом. Система управления – это совокупность объекта управления и устройства управления, взаимодействие которых приводит к выполнению поставленной цели управления. Все технологические процессы на производстве являются объектами управления. Управление техпроцессом, оборудованием, транспортом – это выполнение алгоритма управления. Технологические процессы делятся по характеру на непрерывные, периодические и дискретные. Непрерывным – является техпроцесс, в котором конечный продукт вырабатывается лишь тогда, когда поступает сырье, энергия, расходные материалы и т.д. В периодическом процессе за сравнительно короткий промежуток времени (часов, дней) вырабатывается ограниченное количество продукции. Сырье и полуфабрикаты вводятся строго заданными дозами и в строго заданной последовательности. Операции обработки регламентированы. Конечная продукция появляется только после выполнения всех условий и операций. Примеры: выплавка стали в кислородных конверторах, выпечка хлеба, полевые работы и т.п. Дискретные техпроцессы характерны для машиностроения, приборостроения, легкой промышленности и отличаются наличием множества компонентов, качество которых необходимо контролировать, чтобы конечный продукт отвечал заданным стандартам. Например, сборка. Целью управления технологическим процессом является поддержание в заданных пределах всех условий, необходимых для получения выходной продукции заданного качества и в требуемых количествах (рис.1.1). Управление должно также обеспечивать максимальную экономическую эффективность и минимальное отрицательное воздействие на окружающую среду.
Рис.1.1. Обобщенная схема управления: Д1…Д3 – датчики – приборы, воспринимающие изменение параметров
Изменение внешних условий должно вызывать компенсирующее изменение соответствующих параметров технологического процесса для сохранения постоянного уровня качества конечного продукта. При ручном управлении человек принимает информацию, перерабатывает ее, принимает решение и выполняет регулировочные действия. Если отдельные операции поручить специальным устройствам, процесс управления будет автоматизированным, т.к. человек будет принимать окончательное решение. С передачей всех функций человека автоматическому управляющему устройству получим полностью автоматическую систему управления. Набор датчиков исполнительных механизмов, АЦП и ЦАП, устройства, передающие по одиночным проводам дискретные сигналы типа «включить-выключить» и т.п. образуют систему связи УЭВМ с объектом управления. Во многих автоматических системах управления используется принцип отрицательной обратной связи, когда регулируемое значение того или иного параметра (скорости резания) сравнивается с заданным значением. В зависимости от вида оборудования микро – ЭВМ может использовать различные принципы числового программного управления оборудованием. Большинство динамических объектов работают непрерывно (в непрерывном времени). Их входные и выходные сигналы также существуют непрерывно. Используются термины аналоговые сигналы, аналоговые регуляторы и т.п. С появлением высоконадежных микропроцессоров и микро ЭВМ вместо аналоговых регуляторов стали применять цифровые. Микро ЭВМ работает при этом в режиме прямого цифрового регулирования (ПЦР). Особенностью этого режима является необходимость сопряжения непрерывного процесса в объекте управления с дискретным характером работы микропроцессора. Переход от непрерывных сигналов к дискретным и обратно решается применением АЦП и ЦАП. ЭВМ воспринимает и выдает информацию порциями, т.к. для каждой операции нужен квант времени, а для хранения каждой цифры – ячейка памяти. Даже с увеличением скорости до бесконечности возникнут проблемы с объемом памяти. Кроме того, обработать в реальном масштабе времени большой объем памяти машине не хватит быстродействия. Поэтому в системах цифрового регулирования машина с помощью АЦП отбирает себе для работы лишь отдельные отсчеты сигнала. При этом часть информации об исходном сигнале теряется, причем тем больше, чем меньше частота отсчетов. Таким образом, при разработке схемы цифрового регулирования должны учитываться не только динамические свойства объекта, но и используемая частота отсчетов. В системах цифрового регулирования интерфейс между микро ЭВМ и объектом управления обязательно содержит блоки АЦП и ЦАП. Вне зависимости от характера технологического процесса можно выделить типовые связи с ОУ (объектом управления): вывод и ввод релейных сигналов (или цифровых кодов), вывод и ввод аналоговых сигналов.
Методы синтеза схем управления Действие автоматического устройства можно описать функциональными зависимостями между входными и выходными величинами. При решении задач программного и логического управления приходится синтезировать схемы, описываемые уравнениями трех видов - обыкновенными невременными Булевыми функциями, которые характеризуют работу различных комбинационных схем:
- временными Булевыми функциями, характеризующими поведение схем, работа которых зависит от дискретного времени:
- рекуррентными Булевыми функциями, отражающими поведение схем с обратной связью или конечных автоматов:
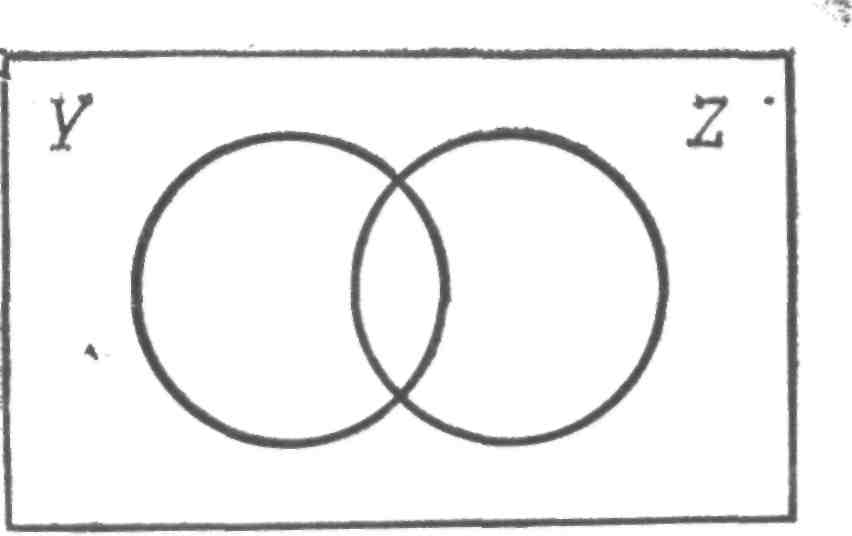
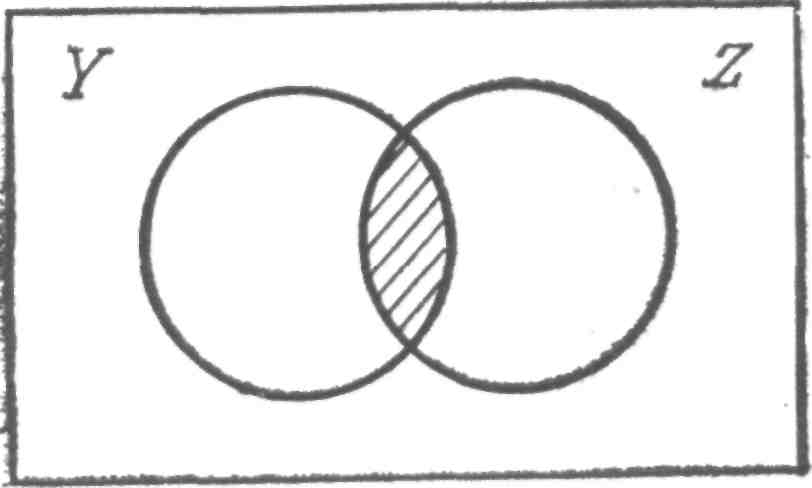
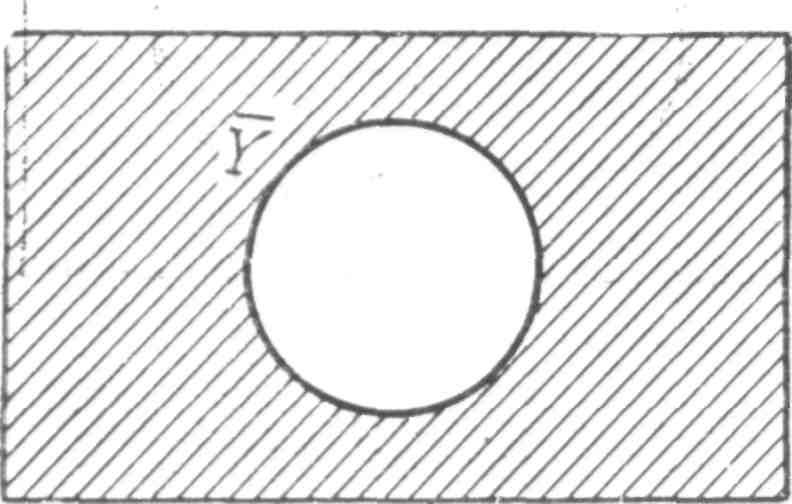
F 30 = a F 3 =0 при t < 0 Xi (i =1, 2, 3, …, n) – двоичные аргументы, принимающие значения «0» или «1»; t – дискретное время, принимающее любые целочисленные значения в интервале 0 £ t £ S -1 r = 1, 2,…, t k = 0, 1, 2, …, t F 30 – начальное значение функции F 3 t при t = 0. Синтез схем, описываемых функциями F 2 и F 3 сложнее, чем функцией F 1, поэтому иногда специальными математическими методами, например, заменой переменных функцию F 2 можно свести к системе функций вида F1. В некоторых простых случаях функции F 3 можно также свести к системе функций F 1 с добавлением соотношения, описывающего многократный элемент задержки. При построении комбинационных схем систем управления приходится решать задачу минимизации исходной Булевой функции. Используются чаще всего приложения Булевой алгебры и карты Карно. В алгебре переключательных схем имеются по существу всего три основные операции. Другие операции могут быть построены как их комбинации. Чтобы проиллюстрировать смысл этих основных операций, рассмотрим прямоугольник, представляющий множество всех элементов, к которым эти операции применимы. Подмножество точек прямоугольника может быть изображено кругом внутри него. Два подмножества Y и Z представляются в виде двух кругов внутри одного и того же прямоугольника (рис. 1.2). Исходя из такого изображения, называемого диаграммой Венна, может быть определена операция И, обозначаемая также символом ×. Заштрихованная область на рис. 1.3 представляет объединение подмножеств, описываемое выражением Y×Z, и является графической иллюстрацией определения операции И.
Рис. 1.2 Множества и подмножества Рис. 1.3 Изображение операции И, Y × Z Операция И относится к основным операциям алгебры логики, поскольку обеспечивает выбор определенной минимальной области. Под минимальной областью здесь понимается множество точек с определенным сочетанием состояний принадлежности этих точек множествам Y и Z и их дополнениям `Y и `Z. Минимальные области являются графическими аналогами понятия минитерма. Заштрихованная область на рис. 1.4 представляет действие операции ИЛИ, которая обозначается символом +. Не следует удивляться использованию знака +. На любой клавиатуре, как и в любом типографском наборе литер, имеется достаточное количество знаков для выражения основных операций. Использование знака + для обозначения логической операции ИЛИ является в данном случае результатом договоренности.
Рис. 1.4 Изображение операции ИЛИ, Y + Z Рис. 1.5 Изображение области `Y
Операция ИЛИ применяется для выделения максимальной области внутри прямоугольника, если исключается предельный случай охвата всей площади. Операции × и + ограничены в своих возможностях выделять подмножества. В связи с этим вводится также основная операция НЕ (рис. 1.5). Действие операции НЕ на подмножество Y представлено на этом рисунке заштрихованной областью. Операция НЕ обозначается чертой над символом. Заштрихованная область на рис. 1.5 обозначается как `Y и читается «не Y». Эта операция позволяет распространить действие операций И и ИЛИ на другие подмножества [11]. Булева алгебра Булева алгебра основана Джорджем Булем (1815-1864 гг) и является с середины 30-х годов прошлого столетия основой для анализа цифровых логических схем. Булевой алгеброй называется непустое множество A с двумя бинарными операциями логического умножения Формальное описание работы схемы в виде Булева выражения позволяет построить логическую схему устройства, реализующего заданный алгоритм. Однако сложность минимизации, отсутствие наглядности и возможности контроля всех возможных вариантов реализации алгоритма привело к использованию таблиц истинности и карт Карно для формального описания работы комбинационных логических схем.
Таблица 2.1 Сводная таблица равносильностей Булевой алгебры
2.2 И спользование таблиц истинности Таблицы истинности могут быть однозначно сопоставлены вербальным алгоритмам и приводившимся выше диаграммам. Если принадлежность произвольной точки прямоугольника множеству Y (или Z) считать «истиной» (с обозначением Т или 1), а противоположный случай – «ложью» (F или 0), то таблица истинности для операции И (конъюнкция) может быть изображена в виде табл. 2.2. Таблица истинности для операции ИЛИ (дизъюнкция) приведена в табл. 2.3.
Таблица 2.2 Таблица 2.3 Таблица истинности для операции И Таблица истинности для операции ИЛИ
В этих таблицах представлены четыре различные комбинации случаев принадлежности (или непринадлежности) точки множествам Y и Z. Таблица истинности – наиболее полный формальный метод описания того, как работает логическая схема. Однако, описание работы схем с помощью таблиц истинности не только громоздко, но и, являясь первой ступенью синтеза любого цифрового устройства, не содержит описания его работы в минимальной форме, необходимой для облегчения анализа возможностей интегральных схем для конкретных приложений. Для дальнейшего анализа и синтеза логической схемы необходимо преобразовать информацию в форме таблицы истинности в Булево выражение. Для записи в дизъюнктивно нормальной форме выделяются те комбинации переменных строки, которые дают логическую «1» на выходе. Аналогичным образом можно построить таблицу истинности по Булеву выражению. Таблица истинности и Булево выражение по разному описывают принцип действия одной и той же логической схемы. Например, если имеется три датчика А, В и С, а включение электродвигателя или другого исполнительного устройства происходит при срабатывании датчиков В и С или датчика А, то формальное описание данного вербального условия работы можно представить в виде таблицы истинности для трех переменных (рис. 2.1), которому соответствует Булево выражение в нормально-дизъюнктивной форме
Рис.2.1. Таблица истинности для Булева выражения
Необходимо учитывать все возможные комбинации входов, которые дают логическую единицу в таблице истинности. Например, минимизированное Булево выражение
Рис.2.2. Таблица истинности для Булева выражения
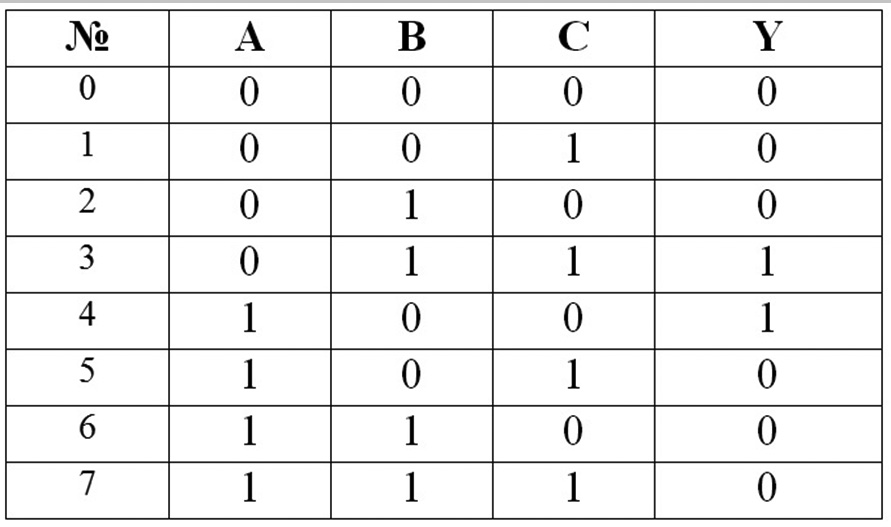
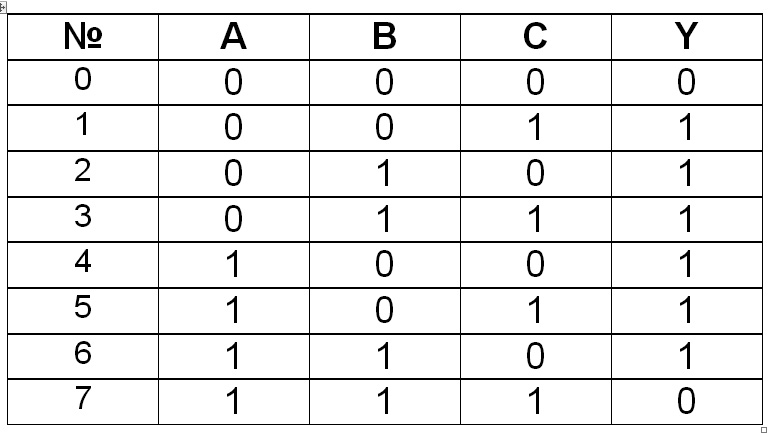
В другом примере требуется обеспечить управление исполнительным элементом Y так, чтобы он срабатывал при наличии сигналов от любых одного или двух из трех датчиков А, В, С. В данном случае формализация словесного алгоритма в виде таблицы истинности представлена на рис.2.3.
Рис.2.3. Формальное описание работы схемы по вербальному описанию
Формальное описание в виде исходного Булева выражения в нормально-дизъюнктивной форме
Рис.2.4. Исходная логическая схема для реализации вербального алгоритма
Используя равносильности Булевой алгебры можно минимизировать исходную функцию Y исх ,
Логическая схема для реализации вербального алгоритма в соответствии с минимизированным Булевым выражением
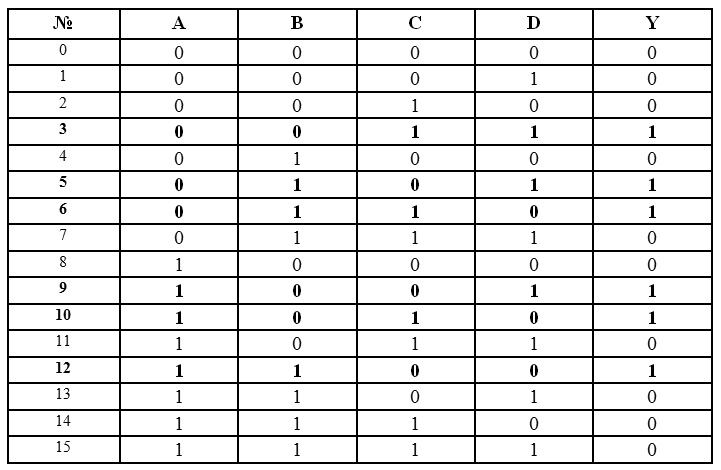
Рис.2.5. Минимизированная логическая схема для реализации вербального алгоритма Если пронумеровать строки таблицы истинности в соответствии с десятичным значением соответствующих двоичных кодов, то можно записать условие работы схемы в виде набора номеров строк, где выходная функция принимает значение 1. Например, функция, записанная в виде Y=∑ (3, 5, 6, 9, 10, 12), может быть представлена соответствующей таблицей истинности (рис.2.6).
Рис.2.6. Таблица истинности
Формальное описание в виде исходного Булева выражения в нормально-дизъюнктивной форме будет иметь вид:
Полученное Булево выражение может быть минимизировано с использованием свойств и аксиом Булевой алгебры и реализовано в виде логической схемы.
2.3 Преобразование входных величин с помощью карт Карно Несмотря на то, что Булевы выражения и таблицы истинности используются для описания функционирования интегральных схем, ни один из этих способов изображения нельзя признать плодотворным при освоении современных методов логического конструирования. Карта Карно́ - графический способ минимизации переключательных (булевых) функций, обеспечивающий относительную простоту работы с большими выражениями и устранение потенциальных гонок. Представляет собой операции попарного неполного склеивания и элементарного поглощения. Карты Карно рассматриваются как перестроенная соответствующим образом таблица истинности функции. Карты Карно можно рассматривать как определенную плоскую развертку n-мерного Булева куба. Карты Карно были изобретены в 1952 Эдвардом В. Вейчем и усовершенствованы в 1953 Морисом Карно, физиком из «Bell Labs», и были призваны помочь упростить цифровые электронные схемы. В карту Карно булевы переменные передаются из таблицы истинности и упорядочиваются с помощью кода Грея, в котором каждое следующее число отличается от предыдущего только одним разрядом. Другими словами в картах Карно при смещении на одну строку по вертикали или на один столбец по горизонтали изменяется лишь одна входная переменная за один шаг. Это исключает так называемые «гонки» или состязания, наблюдаемые при одновременном изменении двух и более входных переменных (рис.2.7).
Рис.2.7. Соответствие номеров строк таблицы истинности и клеток Карты Карно
Таблица истинности для четырех входных переменных имеет 16 возможных комбинаций. На основании следствий алгебры логики упростить Булево выражение не просто. Карты Карно эту задачу значительно облегчают. Например, приведенное ниже исходное Булево выражение в дизъюнктивно нормальной форме можно представить в виде карты Карно, где очевидна возможность минимизации исходного Булева выражения путем объединения рядом стоящих единиц в группы по две и четыре (рис.2.8).
Рис.2.8. Матрица Карно
Шесть единиц нанесены на карту в соответствии шести членам в исходном Булевом выражении. Рядом стоящие единицы объединены в группы из 2х и 4х единиц. Члены, дополняющие друг друга внутри контура, исключаются. Объединив оставшиеся члены функцией ИЛИ, получим минимизированное выражение в дизъюнктивной нормальной форме (ДНФ) (сумма произведений). Количество групп, объединенных контурами определяет число членов минимизированного Булева выражения:
Таблица истинности (рис.2.9) для обоих вариантов одинаковая.
Рис.2.9. Таблица истинности для булева выражения
Логические схемы, составленные в соответствии с исходным и упрощенным выражением будут выполнять одинаковые логические функции, однако, количество элементов меньше, соответственно меньше стоимость, вес, объем, выше надежность. Чем больше размеры объединяющих контуров, тем больше переменных можно опустить. Карту Карно можно как бы «свернуть» в цилиндр с вертикальной осью или с горизонтальной осью или образовать шар, объединяя угловые единицы. Карты Карно рассматриваются как перестроенная соответствующим образом таблица истинности. Карта Карно рассматривается как поверхность фигуры под названием тор. Единичному значению функции соответствуют p-клетки карты Карно. Две соседние p-клетки на карте Карно дают импликанту первого ранга. Например, клетки 1100 и 1101 отличаются только значением переменной x4, следовательно, они дают импликанту Х1, Х2, `Х3. Две соседние импликанты первого ранга образуют импликанту второго ранга. На карте Карно (рис.2.10) соседние клетки образуют две импликанты первого ранга и одну импликанту второго ранга. Минимизированное Булево выражение будет иметь вид Y = Х1, Х2, `Х3 + `Х1, Х2, Х3+ `Х1, `Х4
Рис.2.10.Карта Карно для четырех переменных
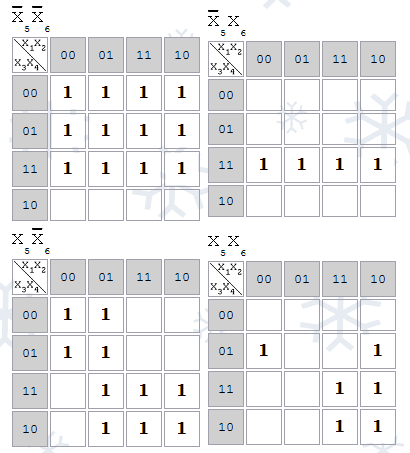
Если функция имеет 5 переменных, то рисуются две карты Карно: для x5=0 и для x5=1. Если 6 переменных - 4 карты так, чтобы в соседних картах соседние клетки имели одинаковые координаты (Рис.2.11). Соседние p-клетки, соответствующие импликанте образуют компактную группу. Количество p-клеток в компактной группе является степенью двойки. Задача минимизации переключательной функции с помощью карт Карно заключается в нахождении импликант высшего ранга (соответствующих компактным группам наибольшей размерности), покрывающих p-клетки функции наилучшим образом.
Рис.2.11. Варианты карт Карно
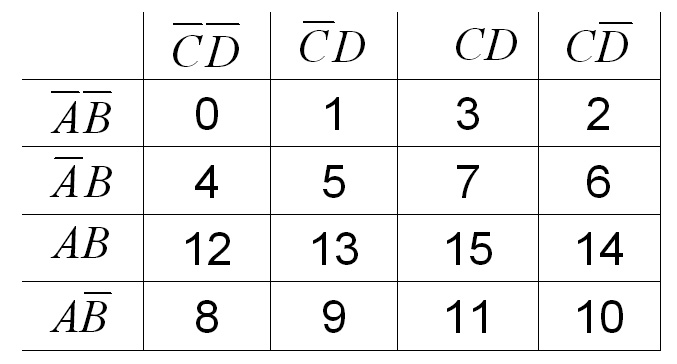
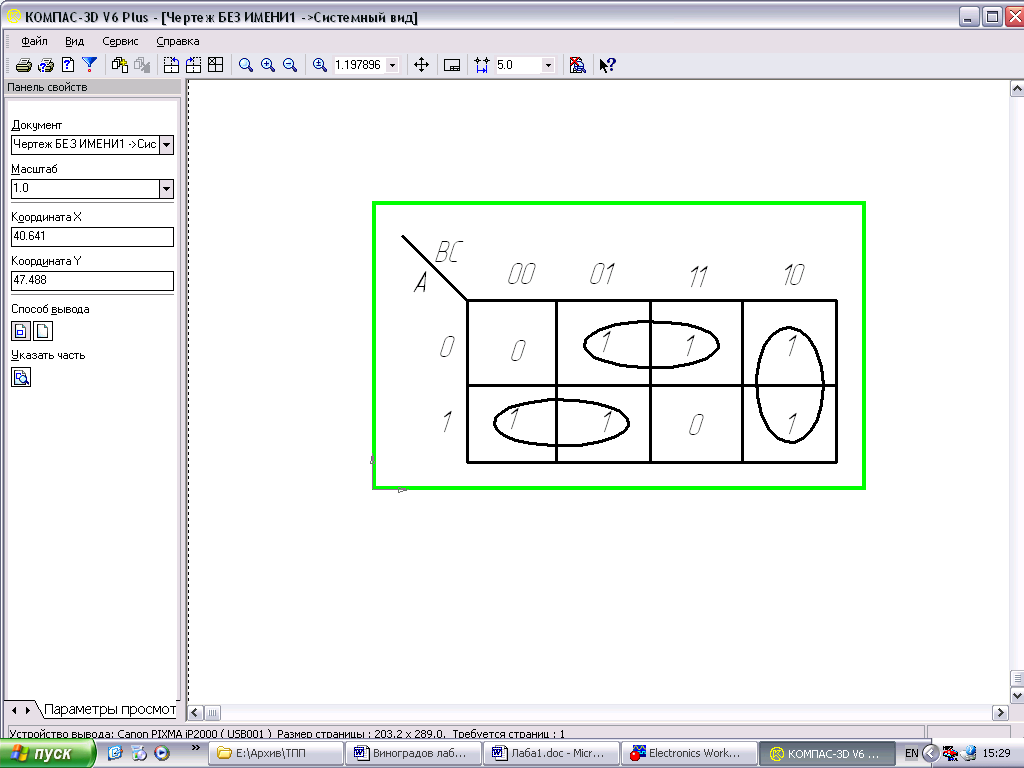
Если на картах Карно выделить все компактные группы наибольшей размерности, то получим минимизированное Булево выражение в дизъюнктивно-нормальной форме (ДНФ). Минимизировать исходное Булево выражение и логическую схему (рис 2.4) гораздо удобнее с помощью карты Карно (Рис.2.12).
Рис.2.12. Карта Карно по таблице истинности (рис.2.3)
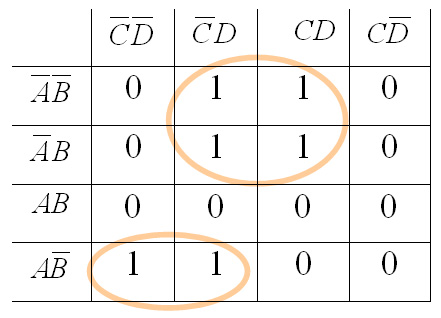
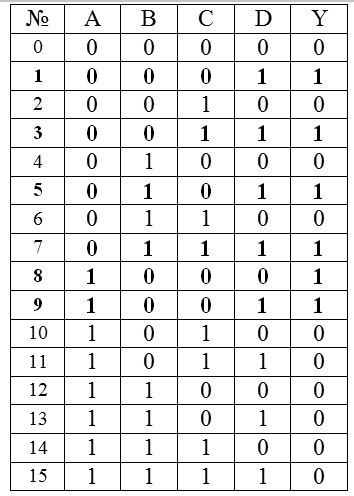
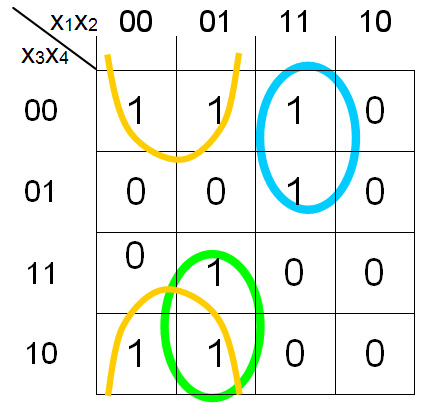
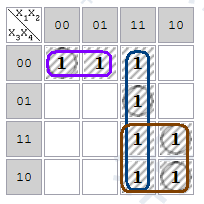
Нетрудно убедиться, что в результате выделения всех компактных групп наибольшей размерности получим минимизированное Булево выражение В качестве примера рассмотрим минимизацию функции 4-х переменных методом карт Карно, где две компактные группы размера 4 и одна компактная группа размера 2 (рис.2.13).
Рис.2.13. Пример карты Карно
Минимизированное Булево выражение в данном случае будет иметь вид Y = `Х1 Ù`Х3 Ù`Х4 Ú Х1Ù Х2 Ú Х1, Ù Х3
Логические элементы
Известно, что математической основой цифровых вычислительных устройств является двоичная арифметика, в которой используются всего два числа - 0 и 1. Выбор двоичной системы счисления диктовался требованиями простоты технической реализации самых сложных задач с использованием всего одного базового элемента – ключа, который имеет два состояния: включен (замкнут) или выключен (разомкнут). Если первое состояние ключа принять за условную (логическую) единицу, то второе будет отражать условный (логический) ноль или наоборот. На рис. 2.14 показаны ключи 1 и 0, управляемые клавишами 1 и 0 соответственно, и вспомогательные устройства в виде гальванической батареи 5 В с внутренним сопротивлением 100 Ом и лампы накаливания на 6 B с мощностью 300 мВт, которые позволяют судить о состоянии ключа: если он находится в положении 1, лама горит (рис. 2.9, а), или не горит, если он находится в положении 0 (рис. 2.14 б). Возможно другое расположение ключей по отношению к вспомогательным устройствам, показанное на рис. 2.15. В этих схемах состояние индикаторов нуля или единицы противоположно показанному на рис. 2.14. При нажатии на клавишу 1 индикатор фиксирует состояние 0 (рис. 2.14, а) и наоборот (рис. 2.14, б). Следовательно: схемы на рис. 2.15 по выходному сигналу (состоянию индикаторных лампочек) обратны (инверсны) по отношению к схемам на рис. 2.14. Поэтому такие ключи называют инверторами.
а) б) Рис. 2.14. Схемы электромеханических имитаторов логической единицы (а) и нуля (б)
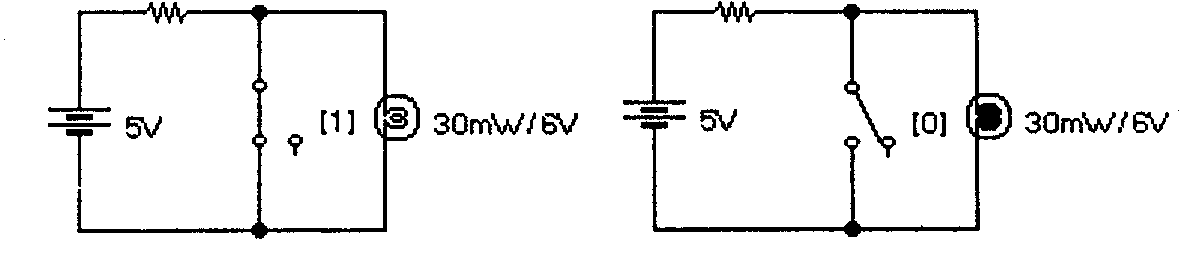
а) б) Рис. 2.15. Электромеханические имитаторы логической единицы (а) и нуля (б) в инверсном режиме
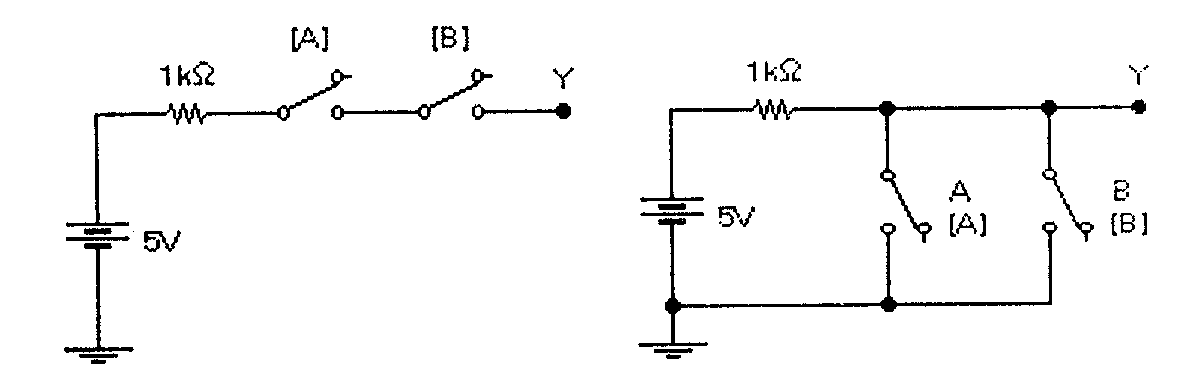
Поскольку в цифровых системах содержится огромное количество ключей (только в одном микропроцессоре их несколько миллионов) и они не могут сообщать друг другу о своем состоянии миганием лампочек, то для взаимного обмена информацией используются электрические сигналы. При этом ключи, как правило, применяются в инверсном режиме в соответствии со схемами на рис. 2.16.
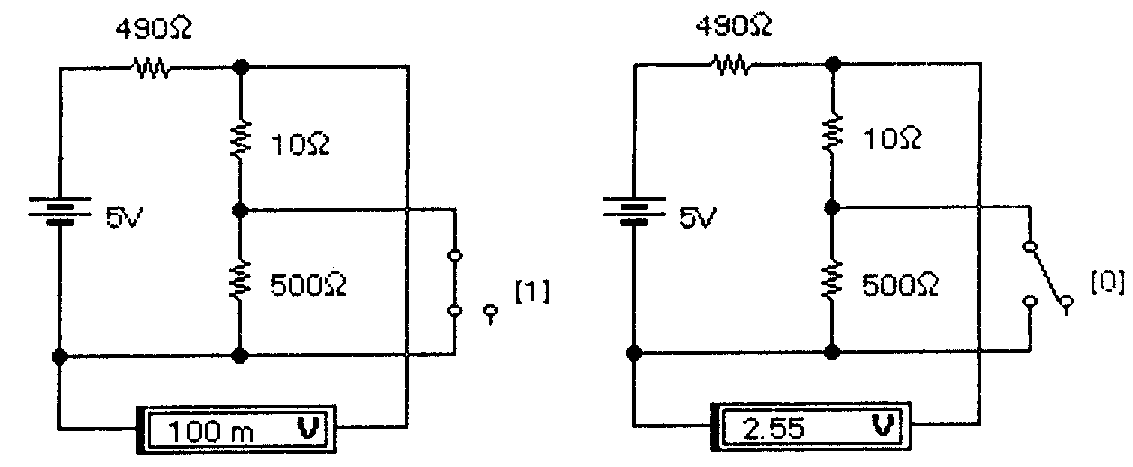
а) б) Рис. 2.16. Электромеханические имитаторы логической "1" (а) и "0" (б) в инверсном режиме с индикаторами выходного напряжения
На рис.2.16 сопротивление 490 Ом имитирует внутреннее сопротивление нагрузки ключа (аналог коллекторного сопротивления в транзисторном ключе), сопротивление 10 Ом — сопротивление замкнутого электронного ключа, сопротивление 500 0м — сопротивление разомкнутого ключа с учетом внешней нагрузки. Как видно из рис. 2.16, наличие на выходе логического нуля (инверсия 1) индицируется напряжением 100 мВ (в практических конструкциях может быть и больше), а наличие логической единицы — напряжением 2,55 В (нормируется на уровне 2,4 В). Электронные ключи проектируются таким образом, чтобы при наихудших сочетаниях входных и выходных параметров ключи могли различать сигналы логической единицы и нуля. В цифровой технике практические аналоги рассмотренных схем принято называть логическими элементами. При этом в зависимости от выполняемых функций каждый элемент имеет свое название и соответствующее графическое обозначение. На рис. 2.17 показаны обозначения базовых логических элементов, принятые в программе EWB.
а) б) в) г) Рис. 2.17. Графические обозначения буферного логического элемента (а), элементов И (AND) (б), ИЛИ (OR) (в), исключающее ИЛИ (XOR) (г) и их инверсные варианты в нижнем ряду (NOT, NAND, NOR, XNOR соответственно)
Электромеханические аналоги двухвходовых элементов И, И-НЕ показаны на рис. 2.18.
а) б) Рис. 2.18. Электромеханические имитаторы
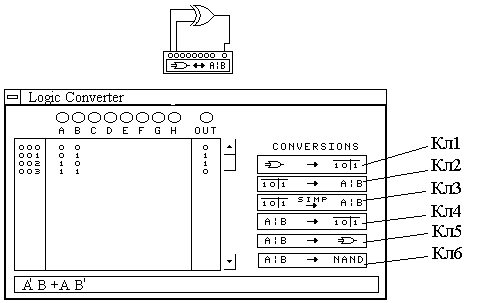
Исследования логических схем целесообразно проводить с помощью имеющегося в программе EWB логического преобразователя. В качестве примера на рис. 2.19 приведена схема для исследования элемента Исключающее ИЛИ. Подключение исследуемого элемента к логическому преобразователю показано на рисунке. Очевидно, что при наличии двух входов возможны только четыре комбинации входных сигналов, что отображается на экране преобразователя в виде таблицы истинности, которая генерируется после нажатия клавиши Кл1.
Рис. 2.19. Исследование логического элемента Исключающее ИЛИ с помощью логического преобразователя
Для получения Булева выражения исследуемого элемента необходимо нажать клавишу Кл2. Это выражение приводится на дополнительном дисплее, расположенном в нижней части лицевой панели, в виде двух слагаемых, соответствующих выходному сигналу ИСТИНА (сигнал логической единицы на выходе OUT). Сопоставление полученного выражения с таблицей истинности убеждает нас в том, что таких комбинаций действительно две, ес
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 166; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.44.207 (0.012 с.) |

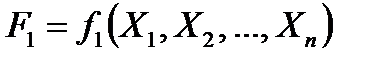 ;
;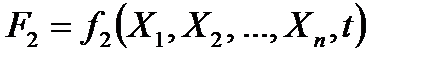 ;
;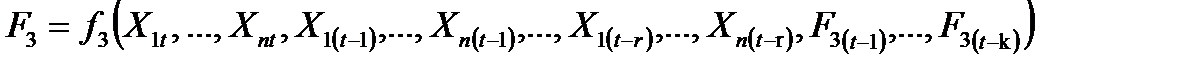

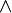 (конъюнкция) и логического сложения
(конъюнкция) и логического сложения 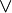 (дизъюнкция), унарной операцией
(дизъюнкция), унарной операцией  (отрицание) и двумя выделенными элементами: 0 (Ложь) и 1 (Истина). Основные равносильности Булевой алгебры представлены в табл.2.1. Использование следствий законов алгебры логики позволяет сократить (минимизировать) логические выражения.
(отрицание) и двумя выделенными элементами: 0 (Ложь) и 1 (Истина). Основные равносильности Булевой алгебры представлены в табл.2.1. Использование следствий законов алгебры логики позволяет сократить (минимизировать) логические выражения.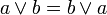
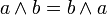
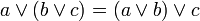
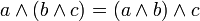
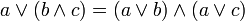 дизъюнкция относительно конъюнкции
дизъюнкция относительно конъюнкции 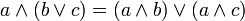
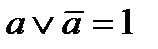
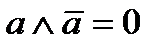
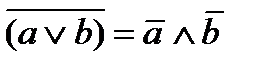
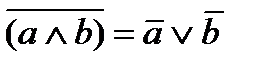
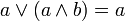
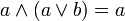
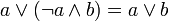
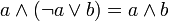
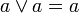
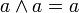
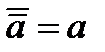

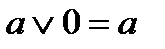
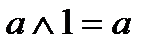
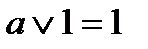
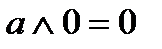
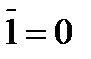 дополнение 1 есть 0
дополнение 1 есть 0 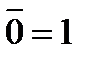
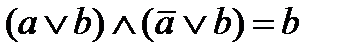
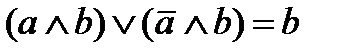
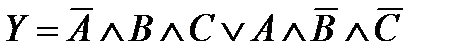
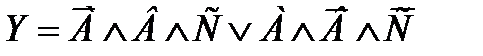
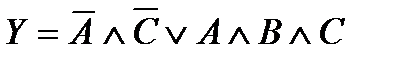 дает не две, а три логических единицы для выходной функции Y в таблице истинности рис. 2.2.
дает не две, а три логических единицы для выходной функции Y в таблице истинности рис. 2.2.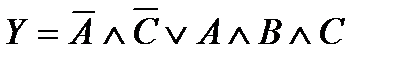
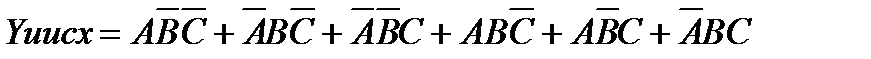 . Логическая схема для реализации вербального алгоритма в соответствии с исходным Булевым выражением будет иметь вид (рис.2.4).
. Логическая схема для реализации вербального алгоритма в соответствии с исходным Булевым выражением будет иметь вид (рис.2.4).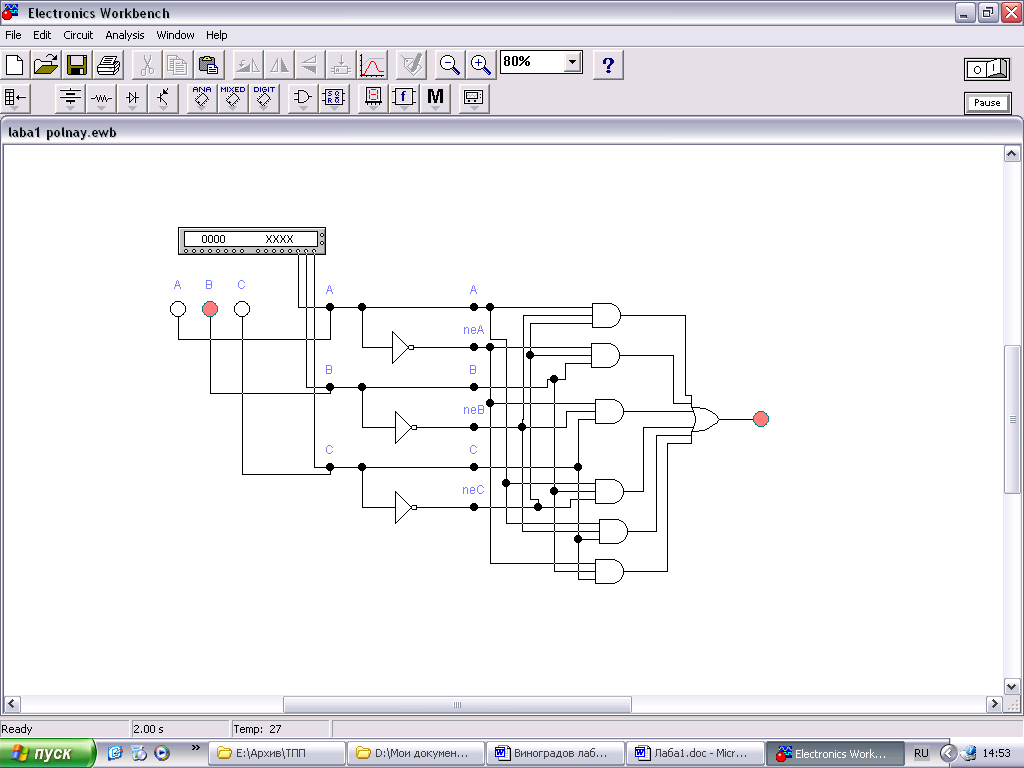
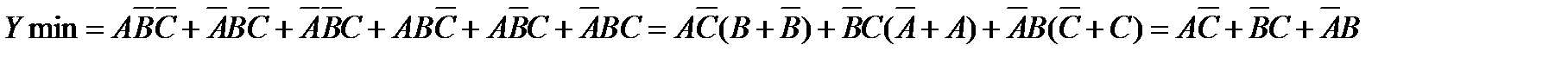
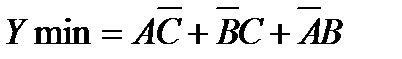 будет иметь вид (рис.2.5). Минимизированная схема работает аналогично исходной, но при этом дешевле и имеет более высокую надежность.
будет иметь вид (рис.2.5). Минимизированная схема работает аналогично исходной, но при этом дешевле и имеет более высокую надежность.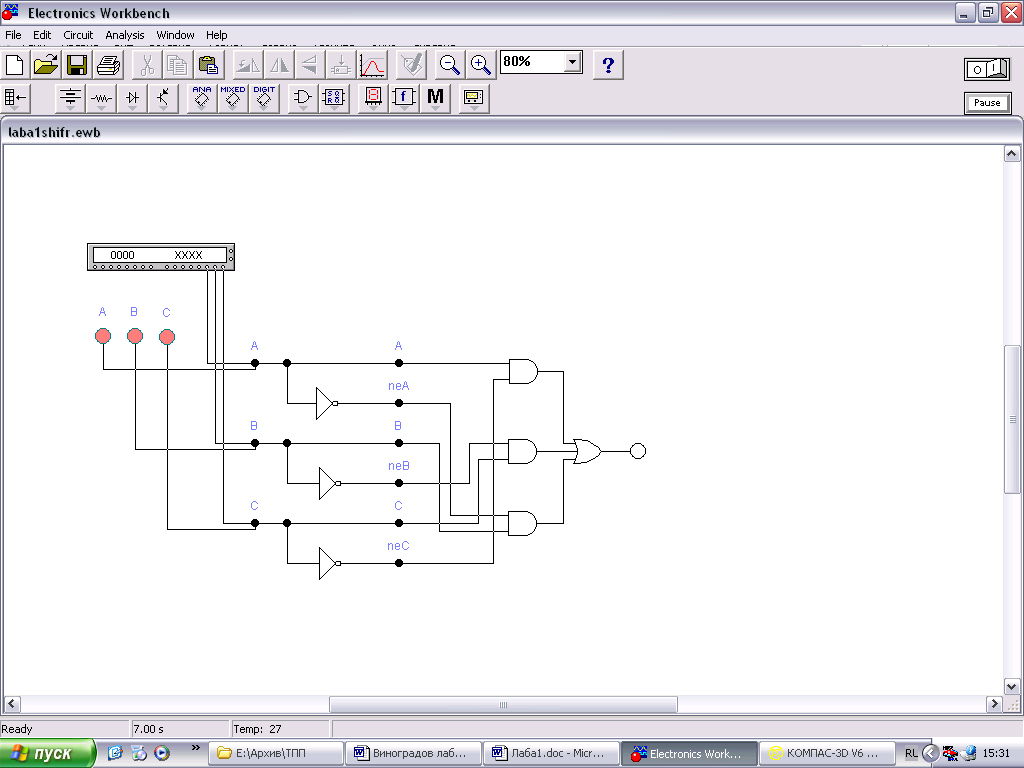
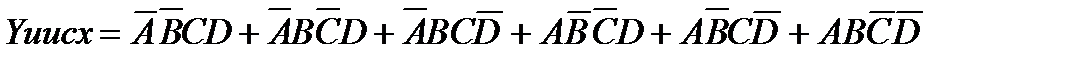 .
.
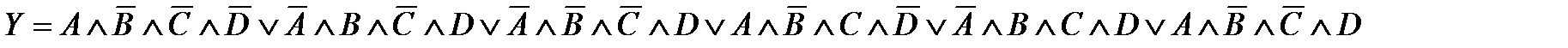
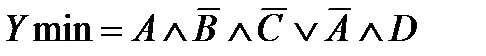
 `
`