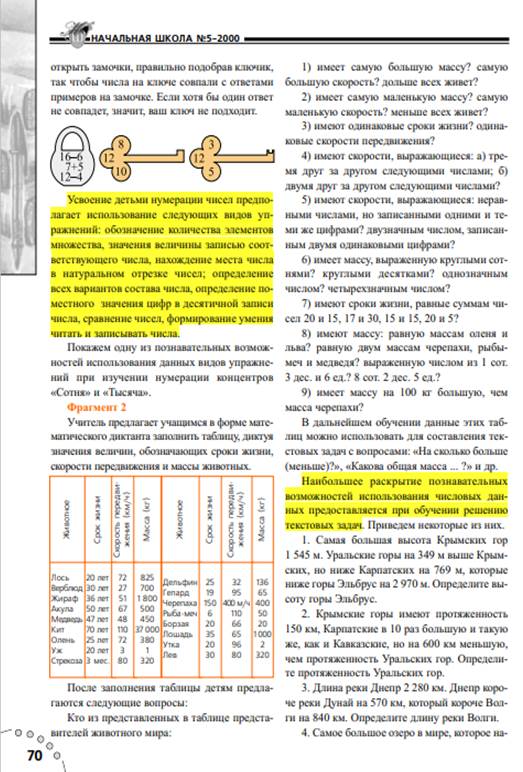
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
К вопросу об изучении величин в начальной школеСтр 1 из 7Следующая ⇒
Статьи Статья 1. «ПЕРСПЕКТИВЫ ИЗУЧЕНИЯ ВЕЛИЧИН И СПОСОБОВ ИХ ИЗМЕРЕНИЯ В РАЗВИТИИ РЕБЁНКА НАЧАЛЬНЫХ КЛАССОВ» https://skachatvs.com/1307418/perspektivy-izucheniya-velichin-i-sposobov-ikh-izmereniya-v-razvitii Аннотация: статья посвящена одному из основных понятий математики – величина. Представлены теоретические основы изучения величин и их измерений в начальной школе. Для учителя предложены рекомендации для организации работы. Ключевые слова: величина, измерение, единица величины, измерительные навыки, разноуровневая дифференциация, изучение темы «величины» в начальной школе Изучение величин на уроках математики в начальных классах имеет большое значение в плане развития младших школьников. Задания с величинами развивают у учащихся пространственные представления, наблюдательность, тактильные и зрительные восприятия и ощущения, вооружают их практическими умениями и навыками, которые в дальнейшем широко применяются в жизни. Знакомство с величинами в начальной школе и их зависимостями помогает созданию у детей целостных представлений об окружающем мире, является основой для дальнейшего изучения математики. Вопросами теории и методики изучения величин в начальной школе занимались такие ученые психологи, как Л. В. Занков, В. В. Давыдов, Н. А. Менчинская, И. И. Якиманская; ученые-методисты – П. С. Исаков, А. М. Пышкало, Н. Б. Истомина, Г. А Корнеева, Л. П. Стойлова и др. Величиной называется особое свойство реальных объектов или явлений, их особенность заключается в том, что данное свойство можно измерить [7]. Как отмечает В.С. Мухина [6], усвоение сенсорных эталонов является одной из сторон развития ориентировки ребенка в свойствах предметов, другой стороной, непрерывно связанной с первой, предстает совершенствование действия восприятия. Формирование у детей младшего школьного возраста представлений о величине является одним из главных разделов формирования элементарных математических представлений. Данное понятие возникло в глубокой древности и на протяжении истории развития человечества подвергалось ряду обобщений и конкретизации. Многие авторы отмечают, что величина включает в себя объем, скорость, массу, число, протяженность и так далее [2]. То есть, понятие величина является обобщенным понятием для класса других математических категорий, связанных между собой определенными признаками и свойствами.
Осознание величины является необходимым компонентом познания человеком объективной действительности, совершенствуется их пространственная ориентировка, содержательнее становится их восприятие; вместе с тем развивается мышление детей, поскольку его объектом становятся новые качества и отношения. Петрова В.Ф. характеризует величину предмета, как его относительную характеристику, подчеркивающую протяженность отдельных частей и определяющая его место среди предметов однородных [8]. Основные задачи изучения величин следующие: – познавательные; – образовательные; – воспитательные; – развивающие [5]. В начальных классах учащиеся знакомятся с такими видами величин, которые определяются только числовым значением, которое рассматривается как отношение одной величины к другой, выполняющей функции мерки. К ним относятся длина, масса, объем (емкость), время и площадь. В профессиональной речи учителя слово «величина» употребляется как минимум в двух значениях: – под понятием «величина» понимается свойство предмета или объекта в разных состояниях, которое можно измерить: ширина, длина, высота, объем, время, скорость, расстояние и др. В данном значении термин «величина» является родовым понятием, к которому как видовые относятся длина, высота, ширина, объем, время и другие; – слово «величина» применяется как количественная характеристика свойства предмета, которая выражается в единицах измерения. В данном значении «величина» используется для выражения числового значения величины как свойства предметов [2]. При знакомстве с величинами важно, чтобы у учащихся сложилось определенное представление о том, что такое величина и как можно ее измерять. Также значительным является связь представления ребенка о величинах с предметами и явлениями окружающего мира и также важно, чтобы, как и понятие числа, понятие «величина» приобрело для него практическую значимость [1]. Изучение практически всех величин в начальном курсе математике изучается по единому алгоритму.
Сначала учитель обращается к опыту ребенка по освоению данной величины, затем происходит сравнение однородных величин с использованием разных методов и приемов, далее учитель знакомит с единицей измерения величины и соответствующим измерительным прибором. Выполняются задания на формирование измерительных умений и навыков, решаются задачи на сложение и вычитание однородных величин, выраженных в единицах одного наименования. На последующих уроках обучающиеся знакомятся с новыми единицами величины, переводят мелкие величины в более крупные и наоборот, складывают и вычитают составные величины. Если изучены арифметические действия второй ступени, то умножают и делят величины на число. В процессе обучения у детей должно сложиться представление о величине как о некотором свойстве предметов и явлений, которое связано с измерениями. В методико-математической литературе, используемой при подготовке учителей начальных классов, этому уделяется достаточно внимания. Однако подлинное происхождение и сущность этих понятий, их взаимосвязь и взаимообусловленность остаются вне сознания подавляющего большинства школьников. При формировании представлений о величине большую роль играет система заданий. В процессе выполнения этих заданий, практических работ на сравнение величин и их измерение учащиеся могут получить глубокое представление о каждой величине, предусмотренной программой. Статья 2. Статья 3. К урокам математики. Автор: Н.Г.Абузярова Выходные данные: журнал начальная школа. 2008 год, 5 выпуск Ссылка: https://n-shkola.ru/storage/archive/1407229985-326604584.pdf Я работаю учителем начальных классов 15 лет, стараюсь ежедневно радовать своих учеников интересными заданиями, систематически использую на уроках математики фактический материал, примеры которого приведены ниже. Работу всегда сопровождаю соответствующими иллюстрациями, что расширяет кругозор младших школьников: 1. Самый толстокожий в мире зверь — нильский бегемот. Толщина его кожи — 2 см 5 мм, а толщина кожи слона — 1 см 8 мм. Так что поговорка «Толстокожий как слон» не совсем справедлива. 2. Самый хищный обитатель морей — меч-рыба. Длина ее тела равна 5 м, вес до 600 кг, а длина необычайно прочного меча — 1 м 50 см. Меч-рыба атакует китов, а также промысловые суда и лодки. 3. Самые высокогорные существа земли — это пауки. Они живут на высоте 7500 м. Для сравнения: птицы могут обитать на высоте 4500 м, а некоторые виды бабочек — 6000 м. Статья 4.
Статья 5. О моделировании при изучении величин в начальных классах Автор: А. П. Ткачев https://n-shkola.ru/storage/archive/1407237508-1759418027.pdf Модели и моделирование в неявной форме всегда использовались при обучении математике. В настоящее время перед школой стоит проблема более широкого их внедрения, в том числе при обучении математике в начальных классах (В.В. Давыдов, Л.П. Стойлова, Л.М. Фридман и др.). Изучение величин является важной частью курса математики для младших школьников. Вместе с тем оно вызывает у них определенные трудности, особенно при выполнении заданий на перевод величин из одних единиц в другие, на установление соотношений между различными единицами, например: «Сравни 4 га и 4 км2». Если при изучении величин и их единиц в явной форме использовать моделирование, давать ученикам задания на построение моделей величин и их единиц, то можно избежать затруднений. Моделирование также позволяет быстро и легко достигать высоких результатов в обучении и математическом развитии младших школьников. Одним из аспектов явного использования моделирования в обучении является рассмотрение самого процесса моделирования математического объекта, формирования и развития математического понятия как модели. Этот аспект является новым и практически не разработанным в методике обучения математике в начальных классах. Остановимся на его рассмотрении подробнее в отношении формирования у младших школьников знаний о длине и ее измерении. При этом будем придерживаться точки зрения тех психологов и педагогов, которые считают, что в основе понятий, выраженных в слове, лежит образный фундамент, что при решении сложных познавательных задач образное моделирование проблемной ситуации участвует наряду с вербальнлогическими компонентами мышления (Л.А.
Венгер и др.). В большинстве случаев изучение величин младшими школьниками начинается с рассмотрения длины, площади и других величин, что создает основу для формирования обобщенного понятия скалярной вели чины. При этом следует использовать интуитивные представления о величинах как о свойствах реальных предметов. Так, уже в дошкольном возрасте дети могут определить, какой предмет длиннее, а какой короче, какие предметы одинаковы по длине. Однако для того чтобы младшие школьники четко и ярко видели среди других свойств предметов свойство протяженности — длину, полезно рассмотреть с ними НАЧАЛЬНАЯ ШКОЛА. 2006. № 11 82 специально смоделированные ситуации на сравнение свойств, включая свойство протяженности. Для этого удобно использовать специально подготовленные комплекты палочек. В комплекте должны быть палочки одинаковые и разные по цвету, характеру обработки поверхности, материалу изгтовления, длине, толщине, форме сечения и массе. На уроке учитель показывает палочки и проводит беседу об их свойствах. Ученики замечают, что каждая палочка окрашена определенным цветом; какие-то палочки блестящие, а какие-то матовые и т.д. Затем учитель предлагает выбрать палочки белого цвета, подчеркивая, что выбранные палочки одинаковы по цвету. Затем учитель обращает внимание детей на то, что, несмотря на то что палочки одинаковы по цвету, они отличаются друг от друга по каким-либо другим свойствам. Дети находят отличия по длине, материалу и т.д. Затем учитель показывает две палочки, одинаковые по длине, но разные по цвету, одна из которых блестящая, а другая матовая. Хорошо, если эти палочки будут отличаться и другими свойствами: материалом, формой сечения и т.п. Учитель сначала предлагает детям найти, чем различаются эти палочки, а затем обобщает ответы, подчеркивая, что палочки отличаются по цвету и блеску, они изготовлены из разного материала. Далее педагог предлагает ученикам найти одинаковое свойство у этих палочек. Ученики говорят, что у палочек одинаковая длина. Если дети не замечают этого, то учитель проводит сравнение палочек по длине, используя способы наложения и приложения. — Положим перед собой одну
палочку. Приложим к ней (наложим на нее) другую палочку так, чтобы их левые концы совпали. Теперь посмотрим на правые концы этих палочек. Мы видим, что они совпали. Это значит, что палочки одинаковые по длине. Говорят, что у этих палочек одинаковая длина. Вы видите, что эти палочки различаются по цвету, блеску, материалу, из которого они сделаны, но у них есть одинаковое общее свойство: у них одинаковая длина. В ходе проведенной таким образом работы в сознании учеников происходит замена реально наблюдаемого свойства протяженности палочки словом длина и связанным с этим словом мысленным образом линейной пространственной протяженности, т.е. мысленной моделью протяженности реальной палочки. Элементами этой модели являются слово длина (слово мы рассматриваем как знак) и поставленный этому слову в соответствие мысленный образ линейной протяженности. Полученная модель является дочисловой, недостаточно точной. Числовая, более точная и полная, модель протяженности получается в результате измерения длины палочки, например, в сантиметрах. Для этого мы подсчитываем, сколько раз длина в 1 см (единица длины, эталон) укладывается в длине палочки; пусть, например, 7 раз. В этом случае мы говорим, что длина палочки равна семи сантиметрам (7 см). В результате измерения мы реально существующую длину (протяженность) палочки заменили (смоделировали) словосочетанием семь сантиметров Это также мысленная (умственная) модель реальной протяженности (длины) палочки. Элементами этой модели являются словосочетание семь сантиметров и мысленный образ эталона длины в один сантиметр. Эта числовая модель протяженности палочки позволяет воссоздать (отмерить) ее реальную длину, перейти от модели к реальной действительности. Явное использование моделирования при изучении длины позволяет более глубоко осознать ее как реальное свойство материальной протяженности реальных предметов, которое в мысленном (умственном) плане моделируется словознаком длина и связанным с ним мысленным образом линейной протяженности. С другой стороны, толкование измерения длины как приема моделирования позволяет трактовать длину предмета как
число мерок (единиц длины), укладывающихся на протяжении предмета (7 см — длина палочки), т.е. как числовую математическую модель реальной протяженности предмета. Статья 6. Статья 7. Школы г. Владимира и области в течение ряда лет работают по разным учебникам математики, которые получили название развивающие. В средней школе № 19 обучение по программе Н. Б. Истоминой проводится шестой год. За это время накопился некоторый опыт, что позволяет поделиться с коллегами особенностями проведения уроков математики в III классе при изучении наиболее трудной темы курса «Величины». Величина, так же как и число, – основное понятие курса математики начальных классов. Одна из задач темы – формирование у детей представления о величине как о некотором свойстве предметов и явлений, которое связано с измерениями. Учащиеся получают представление о длине, массе, емкости, времени, площади и единицах их измерения. Наибольшее количество ошибок допускают учащиеся при переводе однородных величин, выраженных в единицах одних наименований, в другие, а также при выполнении действий с однородными величинами, выраженными в единицах различных наименований. Для устранения и предупреждения этих ошибок в учебниках математики Н. Б. Истоминой введена тема «Действия с величинами». Основная задача ее не только формирование обобщенных способов действий с величинами, но и стимулирование детей к самостоятельному поиску новых действий при работе с этими понятиями. Учебник исключает однообразие упражнений при формировании понятий о величинах. Каждое задание этой темы побуждает учащихся оперировать учебным материалом, используя такие приемы умственных действий, как анализ, классификация, аналогия и др. Чтобы повысить интерес детей, обобщающие уроки по данной теме чаще всего объединялись одной сюжетной линией. Например, «Путешествие на воздушном шаре», «Космос», «Кругосветное путешествие». На таких уроках ученики не только выполняли задания с величинами, но и получали дополнительные сведения из истории космонавтики, астрономии, животного и растительного мира, географии, истории. Так на одном из таких уроков, совершая путешествие вместе с Машей и Мишей на воздушном шаре, дети узнают, что первый воздушный шар, который поднялся в воздух в 1783 г., изобрели братья Монгольфье. Выясняют, сколько лет воздушному шару? (216 лет.) Сколько это веков? Кто были первыми пассажирами шара? Ученики рассуждают: «Век – 100 лет, чтобы узнать, сколько веков в 216 годах, надо 216 разделить на 100, получаем 2 века 16 лет». Работа организуется так. Класс делится на три команды (на парте заранее разложены квадратики разного цвета: синие – для сильных по успеваемости учеников, зеленые – для средних, желтые – для слабых).
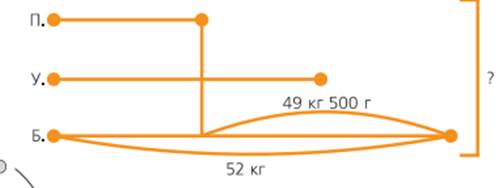
Закончив вычисления, дети находят карточки, соответствующие результатам выполненных действий, переворачивают их и читают имена путешественников: петух, баран, утка. При проверке задания повторяются два способа сложения и вычитания величин: один связан с переводом однородных величин в единицы одинаковых наименований, другой – величины в единицы одинаковых наименований не переводятся. Например, результат сложения 10 км 800 м + 600 м находят по-разному: 1) выражают 10 км 800 м в метрах, а затем выполняют сложение. Дети поясняют: «10 км 800 м – это 10 800 м, сложим 10 800 м и 600 м, получим 11 400 м или 11 км 400 м»; 2) выполняя сложение другим способом, дети говорят: «Сложим 800 м и 600 м, получим 1 400 м – это 1 км 400 м, да еще 10 км, получим 11 км 400 м». Аналогичным образом выполняют действия с величинами в других случаях (17 см + 90 мм = = 17 см + 9 см = 26 см, 17 см + 9 см = = 170 мм + 90 мм = 260 мм). Учитель говорит: «Итак, пассажирами первого воздушного шара были петух, баран и утка. Узнаем их массу. Для этого решим задачу: «Петух в 2 раза легче утки и на 49 кг 500 г легче барана. Какова масса утки, если масса барана равна 52 кг? Какова общая масса пассажиров первого воздушного шара?» Используя схему, составленную к задаче, дети самостоятельно записывают решение:
1) 52 кг – 49 кг 500 г = 2 кг 500 г – масса петуха 2) 2 кг 500 г. 2 = 5 кг – масса утки 3) 52 кг + 2 кг 500 г + 5 кг = 59 кг 500 г – общая масса О т в е т: 5 кг; 59 кг 500 г. С целью соотношения единиц величин на данном уроке дети выполняют следующее задание. Учитель продолжает: «Воздушный шар пролетел над горами: Крымские горы Уральские горы Эльбрус 1 545 м 1 км 899 м 5 633 м». Предлагается сначала записать данные величины в порядке убывания, а затем сравнить их с записанными на доске величинами и выписать равные величины в три столбика. На доске в строчку записано: 18 940 дм, 1 км 545 м, 1 894 м, 15 450 дм, 56 км 33 м, 15 км 45 м, 563 800 см, 18 940 м, 5 км 633 м. Дети выполняют задание:
Выясняется, почему не записали в первый столбик 56 км 33 м; в третий – 15 км 45 м. Ученики дают такие пояснения: «Выразим 56 км 33 м в метрах. В одном километре 1 000 м, значит, в 56 км в 1000 раз больше, т.е. 56 000 м да еще 33 м, получится 56 033 м, не равна величине первого столбца». Аналогично рассуждая, показывают, почему 15 км 45 м нельзя записать в третий столбик. На обобщающих уроках предлагались задания с целью подведения детей к осознанному использованию единиц величин в практике измерения. Например, были предложены следующие задания: 1. Заполни пропуски, определив, какими единицами пользовались при измерении:
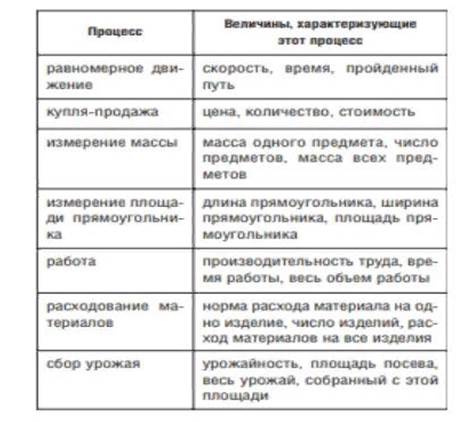
Статья 8. Величина — понятие аксиоматическое. Автор: В.С. Самойлов Выходные данные: журнал начальная школа. 2005 год, 7 выпуск Ссылка: https://n-shkola.ru/storage/archive/1407238695-1207148035.pdf Понятие величина всегда в той или иной степени рассматривалось в курсе арифметики, а затем с 70х годов прошлого столетия и в курсе математики начальных классов. Термин величина стал широко использоваться в курсе математики в начальной школе. В курсе арифметики использовался другой термин — именованное число. В большинстве учебников математики (например, учебники авторского коллектива под руководством М.И. Моро), по которым обучение начинается с изучения нумерации натуральных чисел первого десятка, сравнение величин и действий с величинами, как правило, сводятся к соответствующим операциям над числовыми значениями, т.е. проводятся опосредованно. И лишь в некоторых случаях сравнение производится непосредственно, например, с помощью наложения. Несмотря на то, что величины в указанных учебниках в основном отождествляются с числовыми значениями величин, постепенно у учащихся формируется представление о самих величинах: длине, площади, массе и т.д. При этом четкого обоснования связи величин и чисел (всякую величину a при выбранной единице измерения е можно представить в виде a = kе), непосредственного и опосредованного способов сравнения величин (если две величины находятся в отношении «больше», то и соответствующие числовые значения находятся в таком же отношении) не приводится. Указанные связи постепенно раскрываются в практических действиях над величинами. Совершенно другой подход наблюдается в учебниках математики для начальных классов, написанных в соответствии с системой Д.Б. Эльконина — В.В. Давыдова. По этим учебникам курс математики начинают изучать с величин и их основных свойств. Сложение, вычитание, сравнение геометрических (длина, площадь) и физических величин (масса, время, емкость) проводятся с помощью практических действий: откладывания суммы отрезков, наложения отрезков, сравнения масс с помощью весов, уравнивания масс на весах и др., — в ходе которых выявляются и обобщаются основные свойства величин (сравнимость, возможность складывать, переместительное и сочетательное свойства сложения, возможность вычитать из большей величины меньшую, неизменяемость суммы при замене равных величин на равные, монотонность сложения), которые затем используются в качестве средства для изучения чисел, действий над ними и законов этих действий. Трудность, а во многих случаях невозможность непосредственного сравнения величин позволяет мотивировать введение понятия числа, после чего действия над величинами более обоснованно сводятся к действиям над числовыми значениями величин при выбранной единице измерения. Таким образом, понятие величины как одно из важнейших математических понятий может служить теоретической основой для введения понятия числа и изучения действий с числами. При сравнении методик формирования понятия числа в различных учебниках математики для начальных классов невольно возникает вопрос: что в своей практической деятельности человек начал использовать раньше — числа или величины? Ответ на этот вопрос склоняется в пользу величин, т.к. первоначально человек встретился с необходимостью сравнивать расстояния, длины предметов, например, при изготовлении стрел одинаковой длины. Позднее люди научились считать предметы, а вместе с ними и именованные числа. Другими словами, именованные числа — это форма представления величин. Числа как таковые еще не выделялись, они использовались только вместе с наименованиями. Чтобы получить числа в «чистом виде», необходимо было «оторвать» их от наименований, рассмотреть операции над ними и их свойства. Эта работа была проделана успешно в период образования научных школ в Древней Греции и в странах Дальнего Востока. Обобщению творчества математиков школ Древней Греции посвящен знаменитый труд Евклида «Начала». Здесь приводится и первое аксиоматическое определение величины. Перечислим аксиомы Евклида: · равные одному и тому же равны между собой · если к равным прибавить равные, то и целые будут равны; · если от равных отнимаются равные, то и остатки будут равны; · если к неравным прибавляются равные, то и целые будут не равны; · удвоенные одного и того же равны между собой; · половины одного и того же равны между собой; · совмещающиеся друг с другом равны между собой; · целое больше части Представленная система аксиом в целом не удовлетворяет современным требованиям, к подобного рода системам, т.к. она является зависимой и не является полной (например, четвертая аксиома является следствием второй). Однако математическая теория Евклида до сих пор обладает значительными дидактическими достоинствами: геометрический язык позволяет в тесной связи рассматривать арифметические, геометрические и алгебраические факты; достаточно простой язык позволяет использовать его в школьных курсах математики. После Евклида многие известные математики (Архимед, Герон, Л. Эйлер и др.) пытались определить понятие величины, выделяя те или иные видовые отличия величины. Например, Герон Александрийский (I в.) утверждал, что величина есть все, что может быть увеличено или разделено безгранично, Л. Эйлер (XVIII в.) называл величиной все, что может увеличиваться или уменьшаться. До сих пор существуют попытки определить понятие величины, положив в основу только одно свойство, например, свойство сравнимости. В частности, в свое время о таких величинах писал академик А.Н. Крылов, соотнося их с такими свойствами, как красота, безобразие, храбрость, трусость и т.д. Обобщением различных попыток определить понятие величины является система аксиом замечательного российского ученого, академика А.Н. Колмогорова (1903–1987). В этой аксиоматике первоначальное понятие «величина» является обобщением понятий длины, площади, массы и т.п. Каждый род величины связан с определенным способом сравнения физических тел и других объектов. Таким образом, существующие подходы к определению понятия величины — аксиоматические. Это означает, что не существует какого-либо свойства, которое могло бы служить единственным видовым отличием для величины. Все сказанное говорит об имеющихся возможностях построения достаточно интересной теории скалярной величины для студентов. Понятие скалярной аддитивной величины — это неопределяемое понятие, которое находит свое наиболее полное описание с помощью одной из систем аксиом. Статья 9. Из опыта подготовки студентов к проведению внеклассной работы по математике. Автор: Т.В.Бурлакова Выходные данные: журнал начальная школа. 2005 год, 11 выпуск Ссылка: https://n-shkola.ru/storage/archive/1407238756-300750886.pdf Решение задач-шуток позволит учащимся переключиться на другой вид работы: 1. В корзине 5 яблок. Разделите их между пятью детьми так, чтобы каждый получил по яблоку и одно яблоко осталось бы в корзине. 2. Экипаж, запряженный тройкой лошадей, проехал за час 15 км. С какой скоростью бежала каждая лошадь? 3. Двое играли в шахматы 4 часа. Сколько времени играл каждый? После беседы о зарождении геометрии ученики приступают к решению геометрических задач, способствующих развитию пространственных представлений: 1. Сложите 6 спичек так, чтобы образовались 4 треугольника (сторона каждого треугольника должна быть равна длине спички). 2. Дан кубик, длина ребра которого равна 3 см. Сколько квадратных сантиметров бумаги потребуется, чтобы обклеить ею все грани этого кубика? 3. Даны 2 одинаковых кубика. Длина ребра каждого кубика равна 3 см. Кубики склеены между собой таким образом, что имеют одну общую грань. Вычислите, сколько квадратных сантиметров бумаги необходимо, чтобы обклеить ею всю образовавшуюся геометрическую фигуру. 4. Арбуз разрезали на 4 части и съели. Получилось 5 корок. Может ли такое быть? 5. На какое самое большое число частей можно разрезать блин тремя разрезами? Сколько частей может получиться, если разрезать каравай тремя разрезами? 6. В конверте лежат вырезанные из плотной бумаги квадраты, кружки и треугольники, всего 7 штук. Квадратов в 3 раза больше, чем треугольников. Сколько в конверте кружков? Каждое внеклассное занятие в начальной школе должно содержать задания, проводимые в форме игры. В качестве примера опишем игру «У кого лучше глазомер?». Участники игры берут по листку нелинованной бумаги и на глаз прочерчивают по линейке без деления отрезки заданной длины. Длина отрезков устанавливается играющими. Например, играющие договорились чертить отрезки длиной 5, 8, 14 и 11 см. Выигравшим считается тот, кто точно или почти точно начертит отрезок заданного размера на глаз. Приведенные выше описания внеклассных занятий достаточно полно отражают творческую работу студентов-заочников, которая в дальнейшем позволит выявить и использовать их личные возможности для создания собственных эффективных приемов обучения в начальной школе. Статья 10. Статья 11. Статья 12. Статья 13. Возможности курса по выбору для улучшения подготовки учителя к обучению младших школьников решению задач на процессы. Автор: Е.А.Попова Выходные данные: журнал начальная школа. 2005 г., 2 выпуск Ссылка: https://n-shkola.ru/storage/archive/1408532319-1380778243.pdf Обучение младших школьников решению задач на процессы (движение, работу и др.) сопряжено с большими трудностями. Чаще всего они связаны с тем, что учащиеся не понимают сути процесса, который рассматривается в задаче, не знают характеризующих его величин. Основные процессы, которые встречаются в школьных текстовых задачах, и величины, их характеризующие, представлены в таблице.
Отсутствие правильных представлений об этих процессах приводит к тому, что учащиеся оказываются не в состоянии самостоятельно разобраться в задаче, путаются в ее условии и не могут спланировать последовательность своих действий. При работе с задачами на процессы нужна грамотная, хорошо продуманная помощь учителя, поэтому будущие учителя должны четко знать особенности таких задач, этапы их решения, трудности, возникающие у младших школьников на каждом из этих этапов, и методику обучения, основанную на усвоении приемов действий на каждом этапе решения. Как известно, решение текстовых задач на процессы связано с построением различных вспомогательных моделей. Учитель должен понимать, что построение моделей на этапе анализа значительно облегчает поиск плана решения задачи. Следует отметить, что небольшое количество часов, отводимых в Государственном образовательном стандарте по специальности «Педагогика и методика начального образования» на изучение курса методики обучения математике, не позволяет рассмотреть все сложности и тонкости обучения младших школьников решению задач на процессы. Поэтому студентам выпускных курсов факультета начальных классов предлагается курс по выбору «Обучение младших школьников решению текстовых задач на процессы». Его задачей является расширение и углубление подготовки будущих учителей, полученной в курсе «Методика обучения математике», в области обучения младших школьников решению текстовых задач. В процессе изучения этого курса студенты могут: · расширить знания об особенностях текстовых задач на процессы и различных методических подходах к обучению решению таких задач в начальной школе; · проанализировать процесс решения задачи и рассмотреть каждый из его этапов на примере задач на движение и другие процессы; · освоить методические приемы формирования умений на каждом из этапов решения задач на процессы Содержание курса включает в себя несколько тем. Тема 1. Особенности текстовых задач на движение, работу и другие процессы. Этапы решения таких задач (8 ч). Роль и место текстовых задач в обучении математике в начальной школе. Процессы движения, работы, купли-продажи и др. Величины, характеризующие эти процессы. Зависимости между ними. Тема 2. Особенности методики обучения решению текстовых задач на процессы в различных методических системах обучения математике (8 ч). Методические подходы к обучению младших школьников решению текстовых задач на процессы. Частный подход к обучению решению задач и его особенности. Общий подход и его особенности. Тема 3. Методика обучения решению текстовых задач на процессы, основанная на усвоении приемов действий на каждом этапе решения задачи (10 ч). Приемы формирования умения анализировать задачу, составлять план решения задачи, осуществлять план решения задачи, осуществлять проверку задачи. Тема 4. Методика проектирования урока решения текстовых задач на процессы (8 ч). Подготовительные периоды к решению задач на движение и другие процессы. Проектирование урока с задачами на движение, работу и другие процессы. К концу изучения данного курса студенты должны: · владеть приемами формирования умений, составляющих каждый этап решения задач на процессы; · уметь строить вспомогательные модели к задачам на процессы; · уметь осуществлять логико-математический анализ задач на движение и другие процессы из любого учебника математики для начальных классов; · уметь проектировать урок решения текстовой задачи на процессы; · уметь обнаруживать проблемы, возникающие у младших школьников в процессе решения задач на процессы На проведение данного курса по выбору НАЧАЛЬНАЯ ШКОЛА. 2005. № 2 80 отводится 34 часа. В конце курса проводится зачет. При изучении курса используются различные виды учебной деятельности: · повторяется теоретический материал по математике и методике обучения математике, знание которого необходимо учителю для грамотного обучения младших школьников решению текстовых задач; · анализируется материал различных учебников математики для начальной школы, связанный с обучением решению текстовых задач на процессы; · решаются методические задачи, посредством которых студенты совершенствуют свою подготовку в области обучения младших школьников решению задач на процессы; · выполняется письменная работа по темам, связанным с методикой обучения решению задач на процессы. Нами сформулированы следующие темы письменных работ: 1. Приемы введения понятия «задача на движение». 2. Приемы введения понятия «задача на куплю-продажу». 3. Приемы введения понятия «задача на работу». 4. Приемы обучения младших школьников чтению задач на процессы. 5. Приемы обучения младших школьников составлению графических моделей задач на процессы. 6. Приемы обучения младших школьников составлению кратких записей задач на процессы. 7. Приемы обучения младших школьников составлению плана решения задач на процессы. 8. Приемы обучения младших школьников проверке решения задач на процессы. 9. Обучение младших школьников приему перефразирования на материале задач на процессы. 10. Обучение младших школьников приему перестановки смысловых частей задач на процессы. 11. Приемы использования вещественных (предметных) моделей при работе над задачами на процессы. 12. Приемы использования графических моделей при работе над задачами на процессы. 13. Приемы использования знаковых моделей при работе над задачами на процессы. 14. Приемы анализа и поиска плана решения задач на процессы в учебниках для начальной школы. 15. Методика обучения решению задач на движение в системе... (по выбору студента). 16. Методика обучения решению задач на работу в системе... (по выбору студента). 17. Методика обучения решению задач на покупку-продажу в системе... (по выбору студента). Опыт проведения данного курса в выпускных группах показал, что на преддипломной педагогической практике студенты могут проанализировать методические подходы к обучению решению текстовых задач, которых придерживается учитель класса, где проходит практика; ориентируются в различных программах и учебниках по математике для начальной школы; успешно применяют методические приемы работы над задачами на процессы и добиваются положительных результатов в обучении младших школьников решению указанных задач. Статья 14. Статья 15. Статьи Статья 1. «ПЕРСПЕКТИВЫ ИЗУЧЕНИЯ ВЕЛИЧИН И СПОСОБОВ ИХ ИЗМЕРЕНИЯ В РАЗВИТИИ РЕБЁНКА НАЧАЛЬНЫХ КЛАССОВ» https://skachatvs.com/1307418/perspektivy-izucheniya-velichin-i-sposobov-ikh-izmereniya-v-razvitii Аннотация: статья посвящена одному из основных понятий математики – величина. Представлены теоретические основы изучения величин и их измерений в начальной школе. Для учителя предложены рекомендации для организации работы.<
|
|||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 1152; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.70.203 (0.149 с.) |