
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа. Определение показателя адиабаты при адиабатическом расширении газа методом клемана - дезормаСодержание книги
Поиск на нашем сайте
Цель работы – изучить законы идеального газа, основные положения классической теории теплоёмкости и определить показатель адиабаты методом Клемана-Дезорма.
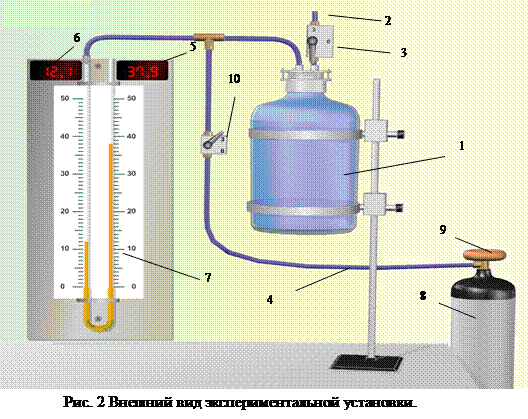
Установка состоит из стеклянного сосуда 1, баллона 8 с редуктором 9, U–образного жидкостного манометра 7 с цифровыми табло 5 и 6. Баллон заполнен сжатым воздухом. Имеется также два крана – впускной кран 10, служащий для напуска газа в сосуд 1 из баллона 8 по магистрали 4, и выпускной кран 3 для соединения сосуда с атмосферой через магистраль 2. Вывод рабочей формулы Рассмотрим метод Клемана–Дезорма. Откроем кран 10 и впустим воздух в стеклянный сосуд 1 (см. рис. 2), после чего закроем кран. При быстром сжатии температура воздуха повышается. Поэтому после прекращения напуска разность уровней жидкости в манометре будет постепенно уменьшаться, пока температура воздуха внутри сосуда не сравняется с температурой окружающего воздуха. Назовем состояние воздуха в сосуде после выравнивания температур состоянием 1. Параметры состояния 1: V 1 - объем единицы массы воздуха; Т 1 - температура воздуха; Р 1 - давление в сосуде. Откроем кран 3и, как только давление в сосуде сравняется с атмосферным, закроем его. Так как расширение происходит очень быстро, то процесс близок к адиабатическому и, следовательно, температура понизится до Т 2. Объем единицы массы воздуха станет равным V 2. Воздух, оставшийся в сосуде, перейдет в состояние 2 с параметрами V 2, Т 2, Р 2 (Р 2 – атмосферное давление). Так как температура Т 2 меньше наружной, то воздух в сосуде будет постепенно нагреваться (вследствие теплообмена с окружающей средой) до температуры окружающего воздуха Т 1. Это нагревание происходит изохорно, так как кран закрыт. Давление воздуха в сосуде увеличивается по сравнению с атмосферным, и в манометре возникает разность уровней h 2, т.е. воздух переходит в состояние 3 с параметрами V 2, Т 1, Р 3. Таким образом, мы имеем три состояния газа с различными параметрами Р, V и Т (см. таблицу 3). В состояниях 1 и 3 воздух имеет одинаковую температуру, следовательно, параметры этих состояний можно связать уравнением изотермического процесса (уравнением Бойля–Мариотта).
Таблица 3 Параметры процесса в трёх состояниях
Переход от состояния 1 к состоянию 2 происходит адиабатически, поэтому параметры состояния связаны уравнением Пуассона (11):
Из уравнений (15) и (16) получим
Прологарифмировав равенство (17), получим
Если давление измерять жидкостным манометром, то вместо р можно писать соответствующую высоту столба жидкости. Тогда можно ввести обозначения
где H – атмосферное давление, h 1 – разность уровней манометра в первом состоянии, h 2 – разность уровней в третьем состоянии. Выражение (18) перепишем в виде
Так как величины h 1 и h 2, выраженные в миллиметрах ртутного столба, очень малы по сравнению с атмосферным давлением H, и, следовательно, дроби
где х - малая величина. Поскольку х 2 и, тем более, х 3 - величины высших порядков малости, ими можно пренебречь, тогда lg(1+ x) @ x и, следовательно,
Пренебрегая величиной h 2 в сумме H + h 2, получим расчетную формулу
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 471; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.127.152 (0.009 с.) |

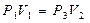 или
или 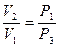 . (15)
. (15)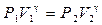 или
или 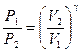 . (16)
. (16)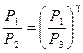 . (17)
. (17)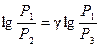 . (18)
. (18)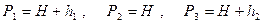
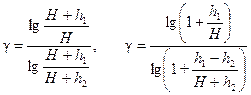 . (19)
. (19)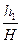 и
и 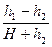 также незначительны, для нахождения величины логарифма можно воспользоваться приближенным выражением
также незначительны, для нахождения величины логарифма можно воспользоваться приближенным выражением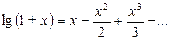 , (20)
, (20)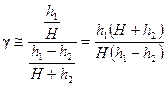 . (21)
. (21)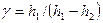 . (22)
. (22)


